Алгоритм расчета хроматической дисперсии одномодовых ов на основе метода смешанных конечных элементов

Представлен алгоритм расчета хроматической дисперсии одномодовых оптических волокон (ОВ), реализующий метод смешанных конечных элементов в векторной постановке. Возможности алгоритма демонстрируются на примерах расчетов для микроструктурированных ОВ (МОВ). Корректность оценок подтверждается результатами их сравнения с известными решениями и экспериментальными данными.

Постановка задачи

Непрерывный рост потребности в увеличении полосы пропускания линий передачи телекоммуникационных сетей определяет интерес к задачам исследования хроматической дисперсии оптических волокон (ОВ). К наиболее точным и универсальным методам прогноза параметров ОВ относится метод конечных элементов (МКЭ) с полностью векторным представлением электрических и магнитных полей [1-6].

Одну из основных проблем применения МКЭ для анализа диэлектрических волноводов вызывает появление нефизических решений – «духов». Такие решения исключаются при использовании метода смешанных конечных элементов [4-8]. Однако применение метода смешанных конечных элементов для решения задачи в векторной постановке требует значительных вычислительных ресурсов. Это, в первую очередь, связано с построением и обработкой разреженных матриц. Проблема усугубляется тем, что точность решения задачи на собственные значения должна быть очень высокой, так как для расчета хроматической дисперсии необходимо знать первую и вторую производные спектральной зависимости постоянной распространения, которые при использовании МКЭ могут быть рассчитаны только путем численного дифференцирования.

Таким образом, для реализации решения задачи прогноза хроматической дисперсии на основе МКЭ необходимо построение алгоритмов, обеспечивающих удовлетворительную точность решения спектральной задачи при относительно умеренных требованиях к вычислительным ресурсам.

В работе представлен алгоритм, реализующий векторный метод смешанных конечных элемен- тов с разложением поля на ребрах и узлах треугольных элементов. Алгоритм не предъявляет специальных требований к вычислительным ресурсам и может быть реализован на обычных персональных компьютерах уровня Intel Core 2 Quad 8200@2.33 ГГц, 8 Гб ОЗУ.

Метод смешанных конечных элементов и алгоритм расчета постоянной распространения диэлектрического волновода

В работе использовался метод смешанных конечных элементов,основанный на известном решении, в котором для представления поперечных компонент поля задавались векторные базисные функции, определенные на ребрах треугольных элементов [7-8 ]. Рассмотрим это решение подробнее.

В общем случае для анализа направляемых мод векторным методом конечных элементов, необходимо дискретизировать ограниченную область волокна с заданными граничными условиями. Для оптического волновода с произвольным профилем показателя преломления, произвольной формой поперечного сечения и идеально проводящими стенками, векторное уравнение Гельмгольца, полученное из уравнений Максвелла, записывается в виде:

Vx^jVx^-^ty = О, (1) где Ф может выступать в качестве вектора напряженности электрического E или магнитного H поля. Показатель преломления материала П_Х,И_Х.Л в направлениях x,y,z соответственно, связан с тензорами диэлектрической [9] и магнитной [p] проницаемости следующим образом:

Px

О

О

О

Ру

О

Чх

О

О

О

Чу

О

о о

Pz

о о

Ч;

Для ф = Е;

Рх = Ру = Pz = U Qx = ¹¹ х ’ Я у = ^Пу ’ Qz = ^Mz • Для ф = Н :

Qx = Qy = Qz = 1, px=\ln;,py = \!n^,pz ^Mn;.

Полагая волновод однородным вдоль оси z, записывают Ф как ф = ф^,уУех^-.№\

Разбивая поперечное сечение волокна на треугольные конечные элементы смешанного типа, компоненты поля в каждом треугольнике представляют как разложение ф = ix • фх + iv ■ фу + i_ • ф- =

[(-;«+i,HrfcL+u^rfc},] ,(3)

где кФХ и {^} значения тангенциальной и аксиальной составляющих поля на ребрах и узлах элементов, {е/ } и {К } базисные функции для реберных и узловых конечных элементов, соответственно.

После подстановки (3) в (1) и применения процедуры метода конечных элементов для анализа направляемых мод была получена система линейных алгебраических уравнений (СЛАУ), которая в общем виде представлена как:

Q^]-,e4^]W={o}.     (4)

Вывод и описание СЛАУ подробно описаны в работах [7-8]. Решая задачу на собственные значения для (4), находят постоянные распространения требуемых мод диэлектрического волновода.

Предлагаемый алгоритм базируется на решении СЛАУ (4). Он включает последовательность следующих операций: задание геометрии сечения ОВ, генерация сетки, задание значений показателя преломления в узлах сетки, формирование локальных и глобальных матриц, решение задачи на собственные значения, обработка и визуализация результатов. Одна из операций, требующая наиболее значительных затрат из-за особенностей работы с разреженными матрицами – сборка глобальных матриц. Можно сократить время решения задачи формирования матриц, если распараллелить процесс. Другой путь – оптимизация алгоритма сборки глобальных матриц. В данном случае использовали алгоритм, согласно которому сначала формируют столбцы матрицы, а затем из них комплектуют глобальную матрицу [9]. Это позволило во много раз сократить время счета. Причем чем больше размер матрицы, то есть чем мельче сетка, тем более выгодным становится такой способ формирования. В результате, при высоких требованиях, предъявляемых к точности расчетов, процесс вычислений занимает секунды, а не часы, как при использовании стандартного подхода.

Учет материальной дисперсии кварцевого стекла

Для определения спектральных характеристик показателя преломления при произвольных значениях концентрации легирующих добавок используется метод учета дисперсионных свойств материала ОВ, основанный на линейной аппроксимации зависимости показателя преломления кварцевого стекла от концентрации легирующей добавки [10]:

И с = n_s + С ■ ^n_D -n_s\        (5)

где n_c – показатель преломления кварцевого стекла с концентрацией С легирующей присадки; ^ D – показатель преломления чистого материала легирующей присадки; n – показатель преломления чистого кварцевого стекла; С – концентрация легирующей добавки.

Расчет хроматической дисперсии

Хроматическая дисперсия рассчитывается по формуле [11-12]:

D=-J^Efc = 2A Л-с dk" Я где P – постоянная распространения; X – длина волны; с – скорость света.

Производные рассчитывались методами численного дифференцирования при использовании аппроксимации спектральных характеристик сплайнами.

Расчет эффективного показателя преломления основной моды МОВ

В целях демонстрации возможностей предложенного алгоритма выполним расчеты для МОВ, отличающихся сложной конструкцией и большим диапазоном изменений значения показателя преломления.

На рис. 1 представлен поперечный разрез МОВ, описанного в работе [13]. Серым цветом отображены области из чистого кремния, белым цветом – заполненные воздухом. МОВ выполнено из чистого кварцевого стекла. «Дырки» заполнены воздухом.

Примеры двух вариантов дискретизации области МОВ показаны на рис. 2, при этом для генерации сетки было использовано 195800 элементов смешанного типа. Первый вариант (рис. 2а) – показатель преломления задается для элемента целиком и при этом сетка формируется так, чтобы грани элементов совпадали с геометрическими границами раздела сред. Второй вариант (рис. 2б) – показатель преломления присваивается вершинам треугольных элементов, а границы раздела сред пересекают грани треугольных элементов случайным образом. В таблице 1 приведены результаты расчета эффективного показателя преломления основной моды МОВ - n_e- P / к . Данные приведены для обоих вариантов в зависимости от числа элементов дискретизации. Там же указано время вычислений для компьютера Intel Core 2 Quad 8200@2.33 ГГц, 8 Гб ОЗУ. Расчеты выполнялись на длине волны 1550 нм.

Таблица 1

Число элементов	Вариант 1 Пе	Вариант 2 Пе	/, с
6 490	1.4520958	1.4515926	19
31 480	1.4520879	1.4518774	123
89 640	1.4520832	1.4520146	583
170 010	1.4520819	1.4520378	1959

Рис. 1. Поперечный разрез МОВ

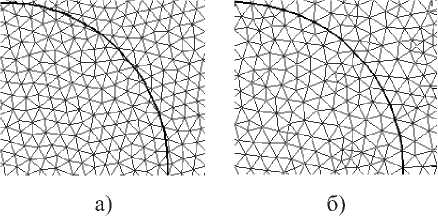
Рис. 2. Варианты формирования сетки

На рис. 3 показано полученное в результате расчетов распределение интенсивности фун- даментальной моды по сечению исследуемого МОВ.

Рис. 3. Распределение интенсивности фундаментальной моды

Рассчитанные по предложенному алгоритму оценки п_е , приведенные в таблице 1, отличаются от представленных в [13] результатов, полученных с помощью КР-метода п_е = 1,4509 и коммерческой программы FIMMWAVE ; менее чем на 0,01%.

Расчет хроматической дисперсии МОВ

Расчет спектральных характеристик хроматической дисперсии был выполнен для МОВ, для которого в работе [14] приведены данные конструкции, а также характеристики экспериментальных образцов, полученные в результате измерений.

На рис. 4 представлено поперечное сечение исследуемого МОВ. Серым цветом отображены области из чистого кремния, белым цветом - заполненные воздухом, а черным – области из кремния легированного окисью германия.

Рис. 4. Поперечный разрез МОВ

На рис. 5 представлены спектральной характеристики хроматической дисперсии дан- ного одномодового МОВ. В частности, приведенные в [14] результаты расчета методом конечных разностей во временной области (FDTD) – кривая 1, и результаты измерений характеристики образца МОВ кривая 2, а также результаты расчета по предложенному алгоритму – кривая 3.

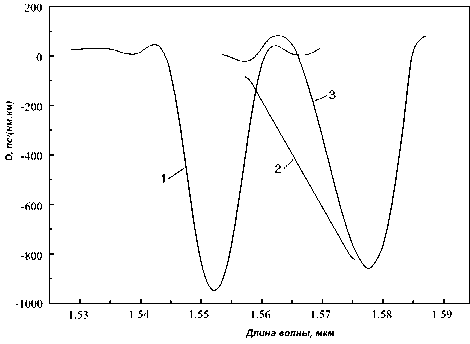
Рис. 5. Спектральные характеристики хроматической дисперсии одномодового МОВ

Как видим, спектральная характеристика хроматической дисперсии 3, рассчитанная по предложенному в данной работе алгоритму, достаточно хорошо соответствует экспериментальной кривой 2 и лучше согласуется с данными измерений по сравнению с представленными в [14] результатами расчетов на основе метода FDTD.

Заключение

Предложен алгоритм расчета хроматической дисперсии оптических волокон, реализующий метод смешанных конечных разностей. На примерах вычислений оценок хроматической дисперсии одномодовых МОВ и сопоставления их с экспериментальными данными показано, что предложенный в работе алгоритм обеспечивает удовлетворительную погрешность оценок при относительно невысоких требованиях к вычислительным ресурсам и может быть реализован на обычных персональных компьютерах уровня Intel Core 2 Quad 8200@2.33 ГГц, 8 Гб ОЗУ.