АЛГОРИТМ РАСЧЕТА ПОЛОЖЕНИЯ И СКОРОСТИ ДВИЖЕНИЯ ОБЪЕКТОВ НА ПЛОСКОСТИ ПО ДАННЫМ С МОНОКУЛЯРНОЙ КАМЕРЫ

Технологии компьютерного зрения активно применяются в различных областях — от автономных транспортных средств до систем безопасности. Такие системы используются для мониторинга пешеходных зон, дорог общего пользования, складских помещений и в управлении беспилотным транспортом. Данные технологии в основном применяются в области анализа окружающей среды для принятия решений в реальном времени. В частности, такие системы могут оценивать траектории движения объектов, определять их скорость и положение, а также прогнозировать потенциальные столкновения или нарушения правил [1–4]. Эти функции особенно важны в условиях высокой динамичности и ограниченного пространства, например, на складских площадках, где необходимо обеспечивать безопасное взаимодействие между погрузчиками, работниками и другими элементами инфраструктуры.

Зачастую для решения задач безопасности перемещения используется оборудование, установленное на погрузчик. В частности, задача предотвращения столкновений решается с помощью парктроников, лидаров или радаров [5, 6]. Однако использование данных технологий имеет ряд недостатков и ограничений:

• •    необходимость наличия на каждом погрузчике и, как следствие, высокая стоимость приобретения и установки;

• •    выполнение ограниченного списка задач — измерение расстояний до объектов и предотвращение столкновений;

• •    сложности при масштабировании.

В то же время на большинстве современных складов уже установлены системы видеонаблюдения, которые могут быть эффективно использованы для решения задач безопасности. Внедрение алгоритмов компьютерного зрения открывает новые возможности для мониторинга и предотвращения столкновений. Однако большое количество установленных камер и отличие складских помещений друг от друга приводит к значительному увеличению объемов и разнообразию данных, которые необходимо обрабатывать. В таких условиях актуальными становятся автоматизированные методы анализа, способные эффективно обрабатывать большие массивы информации и быть устойчивыми. В качестве подобного метода можно использовать искусственные нейронные сети, доказавшие свою эффективность при решении широкого круга задач [7]. Обобщающая способность нейронных сетей и простота установки монокулярных камер позволяет упростить внедрение разработанного решения в существующие склады. В сочетании с имеющимися в погрузчике технологиями предложенный алгоритм позволит расширить список выполняемых задач. Более того, использование данной системы позволяет снизить затраты, исключая необходимость значительных инвестиций в новое оборудование.

В данной работе предлагается алгоритм вычисления положений и скоростей движения объектов на плоскости на основе данных с монокулярной камеры. Для обнаружения объектов интереса используются сверточные нейронные сети. Основной особенностью предложенного алгоритма является автоматический расчет матрицы гомографии, что позволяет обходиться без предварительной ручной калибровки камеры и использования внешней информации о наблюдаемой плоскости. Составление матрицы гомографии осуществляется с помощью распознавания объектов с известными размерами, связанными с наблюдаемой плоскостью. Основными преимуществами алгоритма являются:

• •    использование монокулярной системы вместо радаров и стереокамер;

• •    способность обрабатывать большие объемы видеоданных и потоков с различных камер;

• •    автоматический расчет матрицы гомографии для определения положений объектов на плоскости;

• •    98% рассчитанных средних скоростей лежат в интервале 1 км/ч от эталонных значений.

ОБЗОР ЛИТЕРАТУРЫ

Было разработано множество методов для определения положения и скоростей объектов по данным с монокулярной камеры. В работах [8– 10] представлен метод расчета скоростей движения транспортных средств с использованием трех точек схода. Для определения метрических характеристик полученной сетки необходимо вычислить коэффициент масштаба. В работе [9] для этого используется статистика о средних габаритах автомобилей, которая сопоставляется с габаритами в пикселях. Это может вызывать ошибки, связанные с разнообразием данных в статистике и положением камеры. В статье [10] вместо использования данных статистики авторы предлагают классифицировать марку, модель и год выпуска автомобиля и учитывать его реальные габариты. Данный способ позволяет повысить точность вычисления коэффициента масштаба, однако сложен в реализации, т.к. для обучения классификатора требуется большой объем данных.

В научной литературе также представлены методы, которые для расчета местоположения и пройденного расстояния применяют пред-

варительную калибровку камеры на основе метаинформации о наблюдаемой части дороги [11, 12]. Недостатком такого подхода является требование доступности точных данных о наблюдаемой плоскости, что не всегда возможно.

Помимо этого, ученые предлагают алгоритмы, которые позволяют определять удаленность объектов от камеры на основе распознавания предметов с заранее известными размерами. Например, в статье [13] предлагается алгоритм, где в качестве предмета с известными размерами используется номерной знак автомобиля. Основой алгоритма выступает геометрическая модель системы, а для вычисления скорости используется изменение площади номерного знака на изображении. Основным недостатком данного подхода является необходимость распознавать номер на каждом кадре. Это может быть затруднительно, т.к. номер может быть загрязнен или не виден, а при высоких скоростях и недостаточном освещении его контуры будут размыты. В работе [14] используется сегментация транспортных средств и две зоны интереса. Для каждой зоны на основе найденной маски и истинных размеров автомобиля вычисляется коэффициент PPM , определяющий количество пикселей в одном метре. Далее этот коэффициент используется для расчета пройденного расстояния. Недостатком данного подхода является предварительная калибровка и вычисление коэффициента PPM , от которого напрямую зависит точность вычисления скорости движения объектов.

ОПИСАНИЕ АЛГОРИТМА

Калибровка камеры

Матрица гомографии

Для определения положения обнаруженного объекта на наблюдаемой плоскости необходимо построить соответствие между координатами на изображении и координатами на этой плоскости. Для этого можно воспользоваться матрицей гомографии [15]:

H =

' ^h 11

h 21

h

V *31

h ₁₂

h ₂₂

h 32

h ¹³ h ² 3 ,

.

Выражение (1) представляет собой матрицу 3 x 3, в которой компоненты h 11 , h₁₂, h ₂₁ и h ₂₂ отвечают за поворот и растяжение системы координат, h ₁₃ и h ₂₃ — за сдвиг начала координат, а h ₃₁ и h ₃₂ — за перспективное искажение. Перевод вектора из одной системы координат

в другую осуществляется домножением на матрицу гомографии:

x dst = H • x src , (2)

где x _src — вектор, составленный из координат объекта на изображении, x _dst — вектор, составленный из координат объекта на наблюдаемой плоскости.

Алгоритм определения координат объекта на реальной плоскости

Для составления пар точек src–dst разработан алгоритм определения реальных координат объекта на наблюдаемой плоскости. В его основе лежит распознавание объекта с известными размерами на изображении и использование характеристик монокулярной системы. Для построения модели алгоритма воспользуемся схематическим представлением работы монокулярной камеры, изображенной на рис. 1.

Здесь камера соответствует нижнему треугольнику, основание которого является матрицей камеры с разрешением N пикселей по одной из осей и углом поля зрения γ. Верхний треугольник — зона видимости камеры, в которой на расстоянии h от камеры находится объект с известным размером w. Искомое расстояние h можно найти по формуле:

h = 7-----w7----, tan a 2 - tan a1

где α ₁ и α ₂ — углы, соответствующие правой и левой границам ограничивающей рамки объекта. Положительное направление углов определяется в направлении против часовой стрелки относительно высоты h .

Для расчета удаленности h необходимо определить тангенсы характерных углов α ₁ и α ₂ . Для этого воспользуемся схемой рис. 1. Для произвольного номера пикселя верно:

n tan ai=     , i = 1,2,                  (4)

hcam где hcam — фокусное расстояние камеры. При этом для крайнего значения верно следующее:

γ tan— =

N

Тогда, выразив h _cam из (5) и подставив в (4), получаем

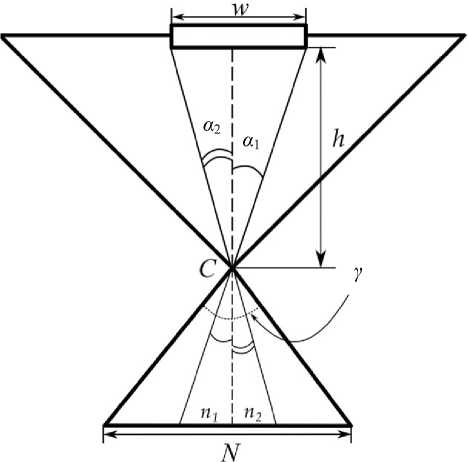
Рис. 1. Геометрическая интерпретация работы камеры. Горизонтальная проекция.

Точка С — объектив камеры с разрешением N и углом поля зрения γ , прямоугольник с шириной w — объект интереса, удаленный от камеры на расстояние h

2n tanγ i tan a =-------2, i = 1,2.          (6)

i N

Использовать удаленность объекта от камеры в качестве одной из координат на реальной плоскости будет некорректно, т.к. данный отрезок не лежит в этой плоскости. Чтобы верно рассчитать координату, воспользуемся схемой работы стационарной монокулярной камеры наблюдения, изображенной на рис. 2.

Здесь H — высота установки камеры от наблюдаемой плоскости; h — удаленность объекта от камеры, рассчитанная по формуле (3); y0 , y2 — координаты границ поля зрения монокулярной камеры; y1   — координата положения объекта интереса на наблюдаемой плоскости. По теореме Пифагора рассчитаем координату y1 :

y 1 = 4h ² - H ².                    (7)

Для определения горизонтальной координаты x объекта интереса на наблюдаемой плоскости определим по формуле (6) тангенс угла α_x для соответствующего положения объекта.

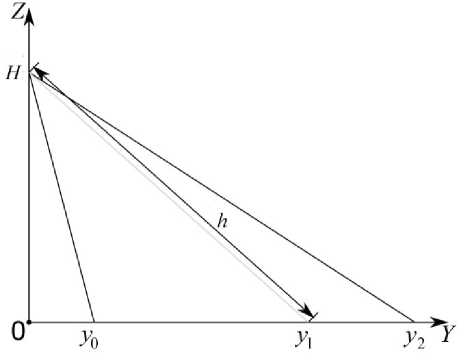
Рис. 2. Схема работы монокулярной камеры. Вид сбоку.

Точка ( 0, H ) — точка установки камеры, у 0 , и y 1 — границы видимости камеры, y ₁ — координата, в которой находится объект интереса на расстоянии h от камеры

Тогда:

x = h • tan a x . (8)

При этом условимся, что вертикальная линия, проходящая через центр изображения, соответствует x = 0, левая часть изображения — x <  0, правая — x >  0.

Следовательно, зная углы поля зрения камеры, разрешение изображения и высоту установки относительно наблюдаемой плоскости, можно определить координаты объекта интереса на данной плоскости, используя координаты объекта на изображении.

Итеративный подбор параметров для расчета матрицы гомографии

В предыдущем разделе описывается алгоритм определения координат объекта интереса на наблюдаемой плоскости. В качестве входных параметров алгоритма используются координаты объекта на изображении, высота установки камеры и ее угол поля зрения. Далее набор найденных пар координат используется для построения матрицы гомографии для области интереса в соответствии с алгоритмом, описанным в разделе "Матрица гомографии". Зачастую при работе с реальными данными с камер параметры, связанные с монокулярной системой, а именно высота установки и угол поля зрения, могут быть неизвестны. В таком случае данные параметры могут быть подобраны итеративно.

Угол поля зрения камеры варьируется от 20° до 130° с шагом 1°, а высота установки — от 2 до 8 м с шагом 0.1 м. Далее выбирается пара значений угла и высоты, которые подставляются в формулы (6), (7) и (8) для перевода координат на изображении в координаты объекта на наблюдаемой плоскости. После расчета всех значений координат найденная пара точек используется для вычисления матрицы гомографии для данного угла поля зрения и высоты установки.

Для выбора итоговой матрицы гомографии используется информация об объекте с известными размерами, который используется для определения координат на наблюдаемой плоскости. В качестве критерия используется условие минимума средней ошибки определения размера объекта на изображении:

^s = N E El d real - d calc I , ^S ^ min, ⁽⁹⁾ где N — количество объектов; d _real — истинный размер данного объекта; d _calc — размер объекта, рассчитанный с помощью матрицы гомографии.

Таким образом можно подобрать параметры камеры, используя информацию о размерах объектов на ней. Данный алгоритм позволяет рассчитать матрицу преобразования для тех случаев, когда конфигурация монокулярной системы неизвестна.

Детектирование и трекинг

Для распознавания объекта на изображении используются алгоритмы на основе машинного обучения. Для того, чтобы разработанную систему можно было реализовать на маломощных вычислителях, таких как Jetson Orin Nano, в качестве детектора была выбрана облегченная архитектура YOLOv8-nano [16]. В отличие от других, данная архитектура обеспечивает высокую скорость обработки изображений в реальном времени при достаточной точности [16, 17].

В данной задаче экспериментальное исследование алгоритма проводилось в складском помещении, по которому передвигались погрузчики с типовым поддоном на вилах. В качестве объекта интереса выступал погрузчик, а объектом с известными размерами выступал поддон. Поэтому в рамках данного исследования для распознавания погрузчика на изображении был обучен детектор YOLOv8-nano, а для поиска поддона — сегментатор той же архитектуры и размера.

Для обучения детектора использовалось порядка 15000 изображений с разрешением

1920 × 1080 пикселей. Данные изображения были получены с различных камер наблюдения, установленных в трех складских помещениях. Перед обучением с целью ускорить работу детектора разрешение входных изображений было уменьшено до 640 × 640 пикселей. Обучение длилось 50 эпох, данные были разделены на тренировочный и валидационный наборы в отношении 75 / 25. На рис. 3 изображен пример данных, которые были использованы для обучения детектора. Ограничивающие рамки отображают результат, выдаваемый детектором.

Для обучения сегментатора поддонов на вилах погрузчика применялись порядка 30000 изображений, вырезанных с кадров в исходном разрешении, которые использовались для обу-

Рис. 3. Пример данных для обучения детектора.

Рис. 4. Пример данных для обучения сегментатора.

чения детектора. Размер данных изображений был предварительно изменен до 640 × 640 пикселей. Обучение длилось 30 эпох, данные были разделены на тренировочный и валидационный наборы в отношении 75 / 25. На рис. 4 изображен пример данных, которые были использованы для обучения. Зеленая область соответствует результату работы сегментатора.

Для расчета скорости движения объекта необходимо хранить историю его положений для каждого момента времени, когда он находится в поле зрения камеры. Для решения данной задачи требуется реализовать работу трекера. В настоящем исследовании использовалась технология BoT-SORT [18], модифицированная для решения поставленной задачи. Основная модификация заключается в введении зоны интереса, которая представляет собой выделенный на изображении многоугольник. Данная зона предназначена для фильтрации детекций удаленных и сложно различимых объектов. Все объекты, распознанные детектором и попадающие в данную зону, передаются трекеру для дальнейшей обработки. Детекции вне зоны интереса не используются в последующих расчетах. Данная модификация позволяет избежать ошибок, которые могут возникнуть при обработке объектов, занимающих слишком малую площадь на изображении или частично скрывающихся за краем изображения. Также в нашей реализации трекера используется фильтр Калмана, реализованный на языке С++ с целью ускорения работы.

Выбор характерной точки объекта и уточнение полученных координат на изображении

При выборе характерной точки для отслеживания важно учитывать перспективу, обусловленную положением камеры. Следует принимать во внимание возможные искажения и выбирать точки так, чтобы минимизировать их влияние при определении местоположения объекта интереса. Наиболее достоверная информация о положении движущегося объекта на наблюдаемой плоскости сосредоточена на нижней грани ограничивающей рамки. Можно выделить несколько ключевых точек на этом отрезке: середина, точки, связанные с объектом, вершины.

Наиболее простым решением является использование середины нижней грани в качестве точки отсчета. Однако этот подход имеет недостаток: позиция этой точки на наблюдаемой плоскости относительно объекта интереса будет изменяться в зависимости от того, где объект находится в кадре.

Другой вариант — это определение характерных точек на объекте, расположенных вблизи или на наблюдаемой плоскости. Этот метод основывается на том, что такие точки движутся вместе с объектом, учитывая перспективу камеры. Примером характерных точек могут служить колеса автомобиля. Недостаток этого метода заключается в том, что часто трудно найти точку, находящуюся близко к наблюдаемой плоскости и всегда видимую камерой.

Последнее предложенное решение заключается в использовании дальнего угла ограничивающей рамки относительно камеры. Перспективные искажения при этом варианте оказывают минимальное влияние на определение положения объекта. Чтобы точно определить положение дальнего угла, можно учитывать положение камеры при ее калибровке или использовать информацию о траектории движения объекта. Например, если движение начинается из левого верхнего угла и заканчивается в правом нижнем, то дальним углом будет правый нижний угол рамки.

Для повышения точности полученных координат разработан алгоритм, который снижает случайные погрешности, возникающие при использовании методов глубокого обучения. Основой метода является усреднение значений координат на основе набора точек. Вначале задается размер окна для корректировки. Затем данный массив заполняется точками в течение нескольких кадров. Как только накоплено достаточное количество точек, по ним строится линейная регрессия, и координаты корректируются ближе к этой линии, не выходя за пределы совокупной средней погрешности. Величина погрешности определяется, исходя из ошибки используемых методов распознавания объектов на изображении.

На рис. 5 показана схема работы алгоритма, где прямоугольники обозначают максимальную коррекцию по каждой оси, а прямая линия — линейная регрессия, построенная по координатам на изображении. Алгоритм состоит из следующих шагов:

• •    определение размера окна для усреднения;

• •    построение линейной регрессии по всем точкам в окне;

• •    коррекция координат на основе полученной регрессии.

Использование данного усреднения позволяет уменьшить влияние погрешности используемых методов для распознавания объектов интереса на изображении. Ограничением данного подхода является требование, что траектория движения объектов в кадре должна быть линейной или изменяться достаточно плавно. Как показывает

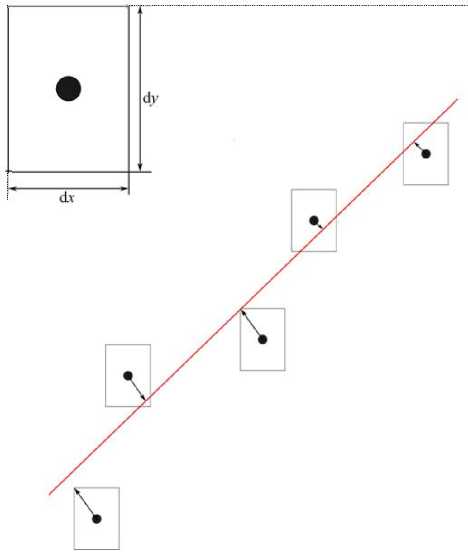
Рис. 5. Коррекция точек расчета.

Окружности — детекции объекта на плоскости изображения, прямоугольники — максимально допустимая коррекция, прямая линия — линейная регрессия

практика, данное ограничение не является жестким. Зачастую инерционность объектов интереса, например погрузчиков или автомобилей, не позволяет им двигаться по неподходящим для данного алгоритма траекториям.

Расчет скорости

После расчета траектории объекта на наблюдаемой плоскости и при наличии соответствующих временных меток можно рассчитать его среднюю скорость. Для этого необходимо разделить перемещение объекта между двумя точками на время, за которое он преодолел данное расстояние:

V avg

P 0 - P 1 ∆ t

где P ₀ , P ₁ — координаты двух точек траектории объекта на наблюдаемой плоскости; Δ t — время, за которое объект переместился от точки P ₀ до точки P ₁ .

Таким образом, для расчета средней скорости движения объекта необходимо хранить историю его положений во времени. Для решения данной задачи используется трекер объектов.

РЕЗУЛЬТАТЫ

Условия эксперимента

Для проверки работоспособности алгоритма и расчета допустимых ограничений была проведена серия экспериментов. В качестве входных данных рассматривалось движение погрузчиков с поддоном на вилах по складскому помещению. Была записана серия видеозаписей проездов. В качестве монокулярной системы использовалась конфигурация с параметрами, указанными в табл. 1.

Полученные видеозаписи были обработаны с применением алгоритма, описанного выше. Было обработано порядка 2 ч видео в реальном времени, которые включают в себя 150 проездов погрузчиков в поле зрения камеры. Для обработки была предварительно создана зона интереса. Данная зона изображена на рис. 6 и соответствует площади, ограниченной белым многоугольником.

Для всех погрузчиков с поддоном на вилах, попавших в данную область, распознавалась маска передней части поддона. Далее маска использовалась для расчета положения погрузчика при использовании алгоритма, представленного в разделе "Описание алгоритма". В качестве наблюдаемой плоскости в данном случае выступала плоскость пола, по которой двигались погрузчики.

Расчет матрицы гомографии

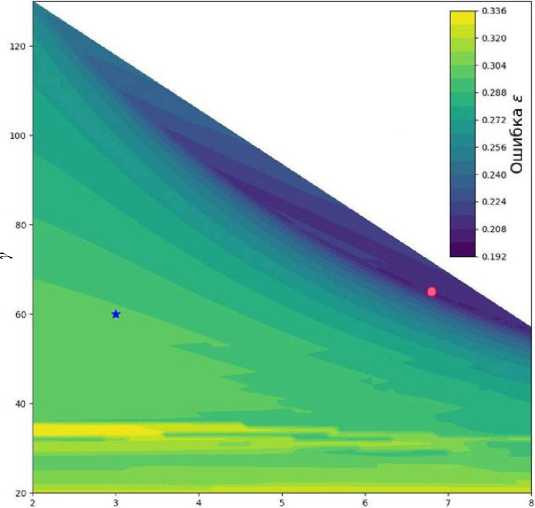
В данном эксперименте был протестирован алгоритм автоматической калибровки камеры путем итерационного подбора параметров, описанного в разделе "Итеративный подбор параметров для расчета матрицы гомографии". Для проведения данного теста мы считаем, что параметры системы (кроме разрешения изображения) заранее неизвестны. Распределение рассчитанной ошибки в зависимости от параметров камеры изображено на рис. 7.

Отсутствие части значений на данном распределении (белая область) связано с тем, что при использовании параметров из этой области полученное расстояние до объекта становилось меньше либо равным высоте установки камеры, чего не может быть .

Табл. 1. Параметры монокулярной системы

Высота установки ( H )	3 м
Угол поля зрения ( γ )	60 °
Разрешение изображения ( M X N )	1920 × 1080

Рис. 6. Зона интереса.

H

Рис. 7. Распределение рассчитанной ошибки при автоматической калибровке.

При этом параметры, которые удовлетворяют критерию (9), с ошибкой £ = 0.197, соответствуют следующим значениям :

Y = 65°,

H = 6.8 м.

Данные значения отмечены точкой на рис. 7. Звезда соответствует истинным параметрам системы, для них значение функции ошибки £ = 0.297.

Подобное отличие рассчитанных параметров камеры от истинных может быть связано со схожестью изображений в зависимости от положения камеры. На рис. 8 схематично изображен описываемый эффект. При данных конфигурациях изображения не будут сильно отличаться друг от друга. Подобный эффект возможен при малых изменениях угла поля зрения y и Y' при сравнении с высотой H и H '. Иными словами, изменение угла поля зрения камеры вносит значительно больший вклад в итоговый результат рассчитанных координат, чем изменение высоты установки. Данное утверждение согласуется с параметрами, полученными в ходе автоматической калибровки. Угол поля зрения γ отличается на 5 ° , что составляет 8% от истинного, а высота установки на 3.8 м ( 227% ).

Рис. 9. Преобразование гомографии. a — истинные параметры системы, б — алгоритм итеративного подбора

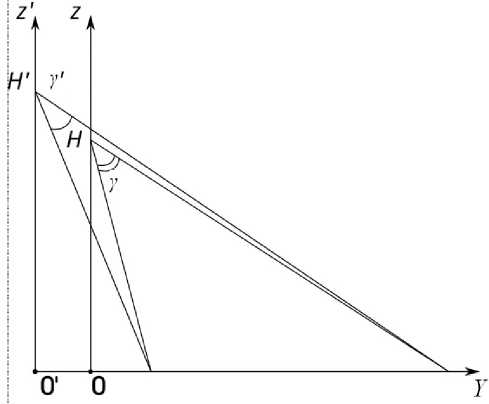
Рис. 8. Разница параметров монокулярной системы.

Далее рассчитаем матрицу гомографии для истинных, указанных в табл. 1, и рассчитанных параметров монокулярной системы. На рис. 9, a, изображена координатная сетка, полученная в результате преобразования (2).

Данная сетка отображает перспективные искажения, вносимые положением камеры. Каждая ячейка обладает размерами 1 × 1 м. Заметно, как площадь ячейки уменьшается при увеличении удаленности объекта от камеры вдоль наблюдаемой плоскости. Сетка, отображающая полученную матрицу преобразования для параметров, полученных алгоритмом автоматической калибровки, изображена на рис. 9, б. Данная сетка является более сжатой по сравнению с той, которая получилась при использовании истинных параметров. Далее рассмотрим влияние выбора рассчитанных матриц при вычислении средней скорости движения погрузчиков.

Расчет средней скорости

Влияние расчета матрицы гомографии

Был проведен эксперимент по вычислению средней скорости проезжающих погрузчиков в поле зрения камеры. Для расчета использовались матрицы гомографии, полученные с использованием истинных параметров монокулярной камеры и с помощью алгоритма автоматической калибровки. В эксперименте скорость погрузчиков, рассчитанная с помощью предложенного алгоритма, сравнивалась со скоростью, полученной с помощью GPS. В качестве результата алгоритма бралось значение, полученное на момент выезда погрузчика из зоны интереса.

На рис. 10 изображено распределение ошибок расчета скорости в зависимости от используемого метода построения матрицы гомографии. Сплошные колонки отвечают за скорости, полученные с использованием истинных параметров камеры, штриховые — при помощи автокалибровки. В качестве характерных точек бралась дальняя от камеры вершина ограничивающей рамки погрузчика. При этом полученные точки корректировались в соответствии с алгоритмом, описанным в разделе "Выбор характерной точки и уточнение полученных координат на изображении". Заметно, что дисперсия значений, полученных с помощью автоматической калибровки, превышает значения, полученные с помощью истинных параметров камеры. В табл. 2 представлена доля рассчитанных

Табл. 2. Влияние алгоритма построения матрицы гомографии на точность расчета средней скорости

Скорости Истинные параметры, % Автокалибровка, % < 0.5 км/ч 0.87 0.67 < 1 км/ч 0.98 0.84 < 1.5 км/ч 1 0.95 < 2 км/ч 1 0.97 скоростей, ошибка которых не превышает определенный порог.

При использовании истинных параметров монокулярной системы 98% рассчитанных скоростей попадают в пределы погрешности ± 1 км/ч, а использование матрицы, полученной с помощью автокалибровки, позволяет достичь метрики в 84%. Следовательно, использование алгоритма автоматической калибровки значительно влияет на точность расчета скорости, однако он все еще может быть применен в ситуациях, не требующих сильных ограничений, и когда параметры системы неизвестны.

Влияние корректировки характерных точек

Рассмотрим влияние алгоритма корректировки характерных точек на расчет скорости. Для расчета матрицы гомографии будем использовать истинные параметры системы. В качестве

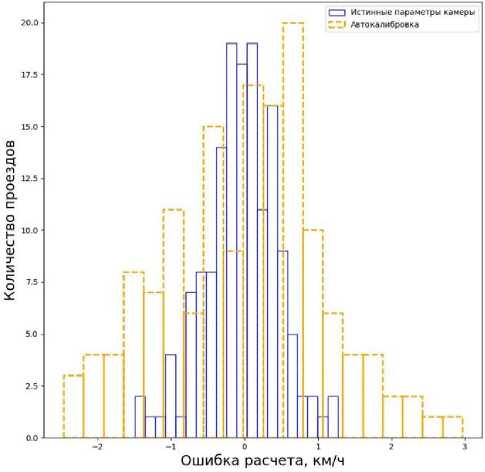
Рис. 10. Распределение GPS-скоростей.

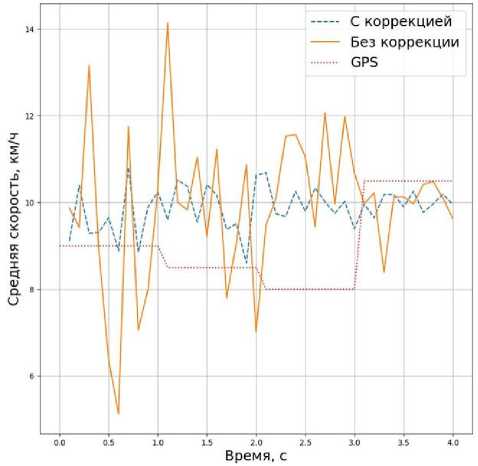
Рис. 11. Коррекция точек расчета при вычислении скорости.

характерной точки будем использовать дальний нижний угол ограничивающей рамки. На рис. 11 изображен результат расчета средней скорости. Сплошная линия соответствует расчету без использования коррекции характерных точек, штриховая — с коррекцией, пунктирная — скорость по GPS.

В данном случае значение средней скорости в каждый момент времени рассчитывается между текущим положением погрузчика на кадре и начальным положением, полученным в момент въезда в зону интереса. Скорость, рассчитанная с использованием алгоритма коррекции, получается более гладкой по сравнению со скоростью, рассчитанной без коррекции.

В табл. 3 представлена доля рассчитанных скоростей, ошибка которых не превышает определенный порог, в зависимости от применения алгоритма коррекции характерных точек.

При использовании алгоритма коррекции удается увеличить точность расчета средней скорости движения погрузчиков. Например, для порога ± 1 км/ч коррекция точек позволяет увеличить долю правильных ответов с 81% до 98%. В результате коррекции точек удается уменьшить влияние случайной ошибки, вызванной алгоритмами распознавания погрузчиков и фронтальной части поддона на изображении.

Влияние выбора характерных точек

Рассмотрим влияние выбора характерной точки на расчет средней скорости движения погрузчиков в зоне интереса. В качестве матрицы гомографии использовалась матрица, полученная с использованием истинных параметров системы. При этом характерные точки корректировались в соответствии с алгоритмом, описанным в разделе "Выбор характерной точки объекта и уточнение полученных координат на изображении". В качестве характерных точек были выбраны: центр нижней грани ограничивающей рамки, центр фронтальной части поддона и дальний нижний относительно камеры угол ограничивающей рамки, в данном

Табл. 3. Влияние коррекции характерных точек на расчет средней скорости

Скорости	С коррекцией, %	Без коррекции, %
< 0.5 км/ч	0.87	0.73
< 1 км/ч	0.98	0.81
< 1.5 км/ч	1	0.9
< 2 км/ч	1	0.94

Табл. 4. Метрика отклонения средней скорости в зависимости от характерных точек

Скорости Дальний угол, % Центр поддона, % Центр нижней грани, % < 0.5 км/ч 0.87 0.80 0.75 < 1 км/ч 0.98 0.93 0.90 < 1.5 км/ч 1 0.96 0.95 < 2 км/ч 1 0.99 0.99 случае это правая нижняя вершина. В табл. 4. представлена доля рассчитанных скоростей, ошибка которых не превышает определенный порог, в зависимости от выбранной характерной точки.

Как и ожидалось, наименьшую точность показал расчет для точек, находящихся на центре нижней грани ограничивающей рамки. Наибольшее количество рассчитанных скоростей при интервале погрешности в ± 1 км/ч было достигнуто при использовании дальнего угла рамки и составило 98%. Для более слабых ограничений разница становится меньше.

ЗАКЛЮЧЕНИЕ

В работе был предложен алгоритм для расчета положений и скоростей движения объектов на плоскости по данным с монокулярной камеры. Основой алгоритма является построение матрицы преобразования точек на плоскости изображения в точки на наблюдаемой плоскости, по которой перемещаются объекты в поле зрения камеры. Для построения матрицы используется информация о реальном размере объекта и параметры монокулярной системы — высота установки и угол поля зрения. Также разработан алгоритм автоматической калибровки камеры. В качестве методов распознавания объектов на изображении использовались нейросетевые детектор и сегмен-татор. Для уменьшения ошибки перспективы проведено исследование по выбору характерной точки объекта на изображении. Чтобы уменьшить погрешность нейросетевых методов распознавания, разработан алгоритм корректировки характерных точек на основе усреднения значений координат. Проведен эксперимент с определением средней скорости движения погрузчиков по распределительному складу в поле зрения монокулярной камеры. Результаты эксперимента показали, что 98% рассчитанных средних скоростей лежат в интервале ±1 км/ч от эталонных значений.