Алгоритм расчета потерь мощности, обусловленных высшими гармониками и интергармониками на основе вейвлет-преобразования

Неизбежный рост доли электроприемников, имеющих нелинейную вольт-амперную характеристику, приводит к искажению синусоидальности формы кривой тока и напряжения в электрических сетях и системах электроснабжения. Как правило, эти режимы являются не экономичными, вызывают дополнительные потери в токоведущих частях, могут приводить к преждевременному выходу из строя электрооборудования. Потери, обусловленные несинусоидальностью, являются причиной дополнительного нагрева токоведущих частей. Действующий ГОСТ 32144–2013 в части несину-соидальности определяет допустимые значения гармонических составляющих напряжения в зависимости от класса напряжения и порядка высшей гармоники. Кроме высших гармоник в электрических сетях возможно возникновение интергармоник, однако их уровень в ГОСТ 32144–2013 «находится на рассмотрении» (п. 4.2.4.2). В странах Европейского Союза уровень интергармоник определяется стандартом IEC 61000-4-7:2, где предельно допустимый уровень интергармоник определен как 0,2 % для каждого номинального напряжения. В США уровень интергармоник регламентируется специальной номограммой стандарта IEEE Std 519 для каждого класса напряжения.

Одной из причин появления в сетях интергармоник являются несинхронные переключения устройств силовой электроники [1]. Источниками интергармоник в системах электроснабжения могут быть преобразователи частоты, дуговые печи, частотно-регулируемый электропривод и др. [1].

Вопросы анализа, моделирования и учета интергармоник вызывают существенный интерес в научном сообществе. В статье [2] приводится имитационное моделирование асинхронного электродвигателя, работающего на переменную периодическую нагрузку. При этом авторы определяют возникающие в обмотках статора высшие гармоники и интергармоники. В результате исследования авторы приходят к выводу о целесообразности применения активных фильтров [2, с. 43]

Зависимость уровня интергармоник в питающей сети системы освещения и кратковременной дозы фликера приведена в работе [3]. В ходе исследований было установлено, что интергармони- ческие искажения влияют на колебания напряжения в сети, что негативно отражается на системах освещения.

Основные расчетные выражения для определения частот интергармоник при работе различных типов преобразователей, включая циклоконверторы, приведены в исследовании [4].

Как отмечают авторы [5], под определение интергармоник «попадают процессы, имеющие совершенно разный генезис», при этом подобные явления пока мало изучены.

Анализ российских и зарубежных нормативных документов, регламентирующих как показатели качества электроэнергии в целом, так и не-синусоидальность в частности, приводится в статье [6]. Авторы считают целесообразным разработку отечественных нормативных значений допустимых пределов гармонических и интергармонических составляющих тока [6, с. 31]

Таким образом, возникает задача оценки негативного влияния интергармоник с целью внесения рекомендаций об их нормировании в электрических сетях России.

• 1.    Основные положения исследования

Математический аппарат вейвлет-преобразо-вания получает все более широкое применение для анализа динамики сложных нестационарных несинусоидальных процессов. Теория вейвлетов применяется для модуляции напряжения на выходе автономных инверторов напряжения [7]. Вейвлет-анализ токов асинхронных двигателей и уровней вибрации позволил авторам [8] произвести оценку остаточного ресурса машины с достаточно высокой (до 96 %) достоверностью. Вейвлет-анализ находит применение для анализа несинусоидальных режимов, в том числе расчета гармоник и интергармоник [9, 10].

В настоящей работе для реализации алгоритма расчета потерь мощности в токоведущих частях от высших гармоник и интергармоник будет использован метод вейвлет-анализа.

В статье [11] авторы применяют частотновременной контур быстрого преобразования Фурье для анализа интергармоник. Применение вейвлет-преобразования позволит упростить решение, предложенное в [11]. В статье [12] представлены разработки метода идентификации интергармоник в сети промышленного предприятия при наличии частотно-регулируемого привода.

Как известно, любая вейвлет-функция представляет собой цифровой фильтр с определенной амплитудно-частотной характеристикой, которая в общем случае определяется типом вейвлета и глубиной разложения при реализации алгоритма вейвлет-преобразования. Таким образом, каждая вейвлет-функция может быть представлена характеристиками цифрового фильтра. Как и любой реальный фильтр, вейвлеты вносят некоторые искажения в полосе пропускания и не полностью подавляют частоты в полосе заграждения. На рис. 1 представлены амплитудно-частотные характеристики вейвлет-функций Ингрид Добе-ши 10 (обозначено пунктирной линией) и 44 порядков (обозначено сплошной линией).

В настоящий момент для решения задач спектрального анализа токов и напряжений при несинусоидальных режимах электрических сетей широко применяется метод преобразования Фурье. В случае анализа нестационарных режимов возникает эффект «растекания спектра», который может быть минимизирован с помощью оконного преобразования Фурье. В соответствии с действующей нормативной документацией [13] для устранения эффекта «растекания спектра» используется принцип группирования гармоник и интергармоник в соответствии с формулой

2     1 2                 N* 2-1     2

Y g , h = T Y C ,( Nh ) - N / 2 +     t Y C ,( Nh ) + k ⁺

²                 k = ( - N / 2) + 1

⁺ 2 Y C ,( Nh ) + N 2 ,                                 ⁽¹⁾

где Y_C ,( _Nh ) _ N2 - среднеквадратичное значение частотной компоненты;

( Nh ) + k - номер частотной компоненты;

Y_{g , h} – результирующее среднеквадратичное значение гармонической группы.

Принцип формирования групп и подгрупп гармоник и интергармоник представлен на рис. 2 и 3.

Для выбора оптимальной вейвлет-функции предлагается совместить гармонические и интергармонические группы, определенные в [13] с полосой пропускания вейвлет-функции таким образом, чтобы узлу a_{j , k} дерева вейвлет-разложения

соответствовала полоса пропускания нижних час-

тот, а следующему узлу a j _{k + 4} дерева полоса пропускания верхних частот вейвлет-функции (рис. 4).

Если в качестве одного из условий выбора оптимальной вейвлет-функции для анализа несинусоидальных режимов электрических сетей принять минимальное среднеквадратичное отклонение исходного сигнала i_k тока (напряжения) от функции тока, восстановленного в результате обратного вейвлет-преобразования i_k , то это позволит говорить о минимальной потере информации о сигнале.

Характерным признаком совпадения полос пропускания и заграждения вейвлет-функций при совмещении гармонических и интергармонических групп в соответствии с рис. 4 может быть энергия спектра, определяемая для каждого узла дерева вейвлет-разложения. Энергия спектра гармонической группы E_n должна быть максимальной именно в границах узла вейвлет-разло-жения a_{j , k} . В таком случае критерий для выбора оптимальной вейвлет-функции может быть записан в следующем виде:

g =

<

Zt (kk - k )2

k =1-- > min;

n

tk

!■ k |²+ Z ЬГ,

E n n = E ;

k = n

k = n

^        ^ ^

zb-k| '-1 к k =-^        j=J k =-^

^Dj , k ²

max.

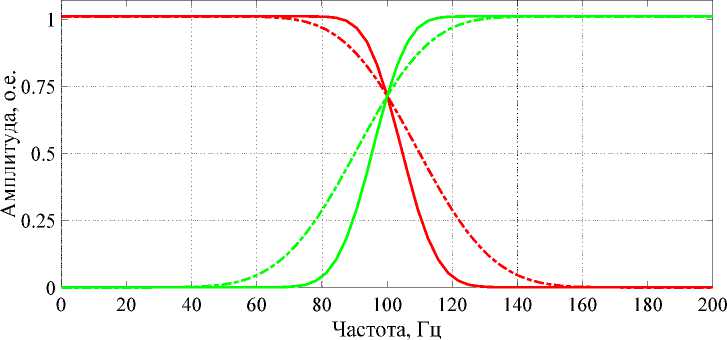
Рис. 1. АЧХ вейвлетов Добеши db10, db44

Fig. 1. Frequency response of Daubechies wavelets db10, db44

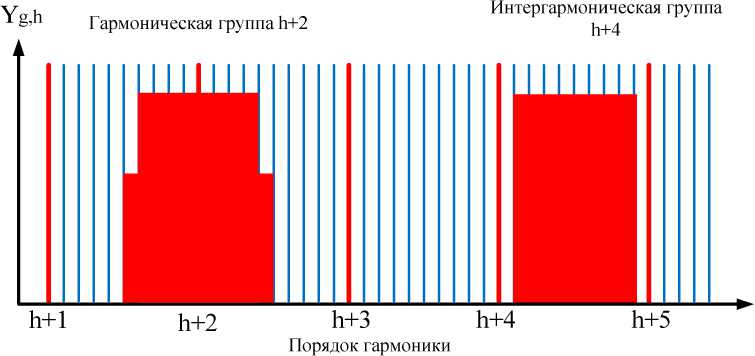
Рис. 2. Принцип образования гармонических и интергармонических групп [13, с. 15] Fig. 2. The formation of harmonic and interharmonic groups [13, p. 15]

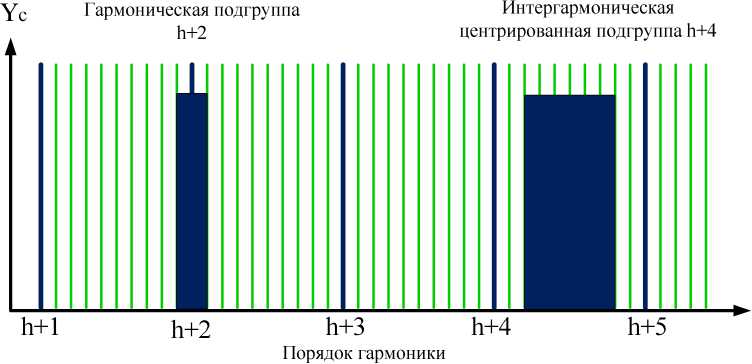
Рис. 3. Принцип образования интергармонических подгрупп [13, с. 17]

Fig. 3. The formation of interharmonic subgroups [13, p. 17]

Частотная локализация узла aj,k

Частотная локализация узла aj,k+i

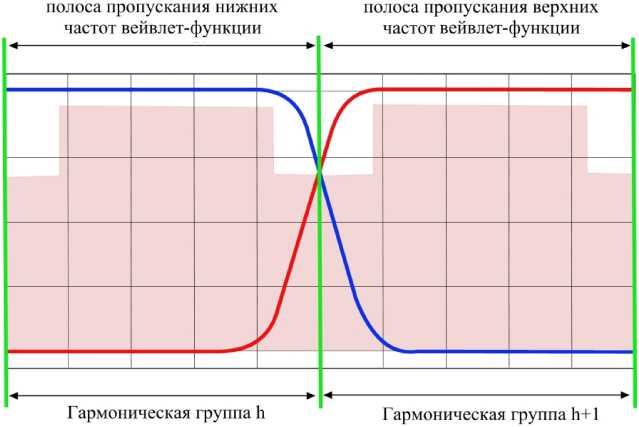
Рис. 4. Совмещение полос пропускания и заграждения вейвлет-функций с гармоническими группами по ГОСТ 30804.4.30–2013 [14]

Fig. 4. The combination of the passbands and the blocking of wavelet functions with harmonic groups according to GOST 30804.4.30–2013 [14]

Предложенный критерий (выражение (2)) позволит на предварительном этапе выбрать оптимальную вейвлет-функцию для расчета действующих значений токов высших гармоник и интергармоник.

• 2 Полученные результаты

Как было отмечено выше, несинусоидальные режимы могут приводить к росту потерь мощности и электроэнергии, а также к повышению температуры токоведущих частей. Необходимость учета интергармоник в расчете потерь мощности определяется в статье [15].

В статье [16] представлен метод, в основе которого лежат преобразования Гильберта, который позволяет проводить спектральный анализ гармоник и интергармоник, при этом производится сдвиг оконной функции и интерполяция.

В зависимости от выходной частоты преобразователя частоты f ₀ спектральный состав тока (напряжения) может быть различным. В общем случае спектр частот может быть представлен в виде основной гармоники и двух боковых частот:

i ( t ) = I m • sin(2 n ft ) + I m • m • sin((2 n f + Q ) t ), (3) где I _m – амплитуда основной частоты, А;

I m • m - амплитуда боковых частот, А;

f – частота питающей сети, Гц;

Q - угловая частота огибающей, рад/с.

Наличие боковых частот вызывает эффект колебания напряжения.

В качестве исходного сигнала в предлагаемом алгоритме используются мгновенные значения токов, которые формирует измерительный прибор. Следует отметить, что частота дискретизации измерительного прибора должна соответствовать теореме Котельникова, в противном случае возможны искажения в процессе цифровой обработки сигналов [17].

В настоящей работе производится модернизация метода, представленного в работе [18] с учетом дополнительных условий выбора оптимального типа вейвлет-функции по выражению (2).

На первом этапе производится вейвлет-преобразование сигнала тока и на основании детализирующих вейвлет-коэффициентов высоких порядков определяются интервалы присутствия той или иной гармонической (интергармонической) составляющей. Участок времени, на котором происходит существенное изменение сигнала, характеризуется значительным увеличением детализирующих коэффициентов (рис. 5).

Аналогичный подход использования детализирующих вейвлет-коэффициентов высоких порядков для определения границ изменения режима при анализе отклонения напряжения был использован в статье [19, c. 133] и в работе [20, c. 276–277].

Далее каждый элемент матрицы тока возводится в квадрат, в результате чего можно записать следующее выражение i2 (t) = Im • sin2 (tot) + Im • m2 • sin2 ((to+Q)t) =

_ 2 I 1        2 I - , 2

= I m '[ 2 + m J + 2 I m

• m • cos Q • t + I _m • m • cos 2 Q t +

, 2 I 2      1 I                    2

+ I_m - \m — — I • cos 2 to t - I_m • m • cos( to - П ) -

2                      1 • m

— Im * m • cos( to + П ) —------ • cos 2 • ( to — П ) —

• — — cos2 • ( to + Q ). (4)

Из выражения (4) видно, что при возведении исследуемой функции в квадрат в сигнале появляется постоянная составляющая тока и частоты Ω, 2Ω, 2ω и др. Практический интерес представляет частота огибающей - Q , что позволит определить частоту интергармоники.

В результате частотной декомпозиции сигнала тока (выражение (4)) и оценки спектральной плотности (метод Уэлча, Барлетта и др.) получаем частоту огибающей Ω, из которой определяется частота интергармоники (рис. 6).

Модернизированный алгоритм расчета потерь мощности от высших гармоник и интергармоник представлен на рис. 7.

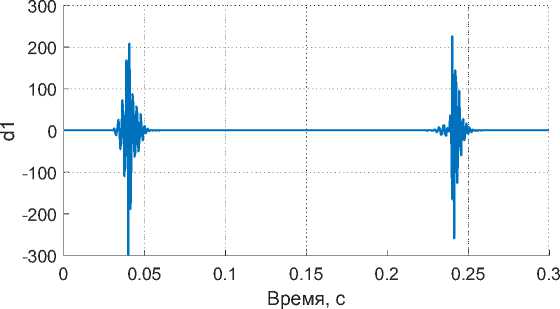
Рис. 5. График детализирующего вейвлет-коэффициента d1

Fig. 5. Detail of the wavelet coefficient d1

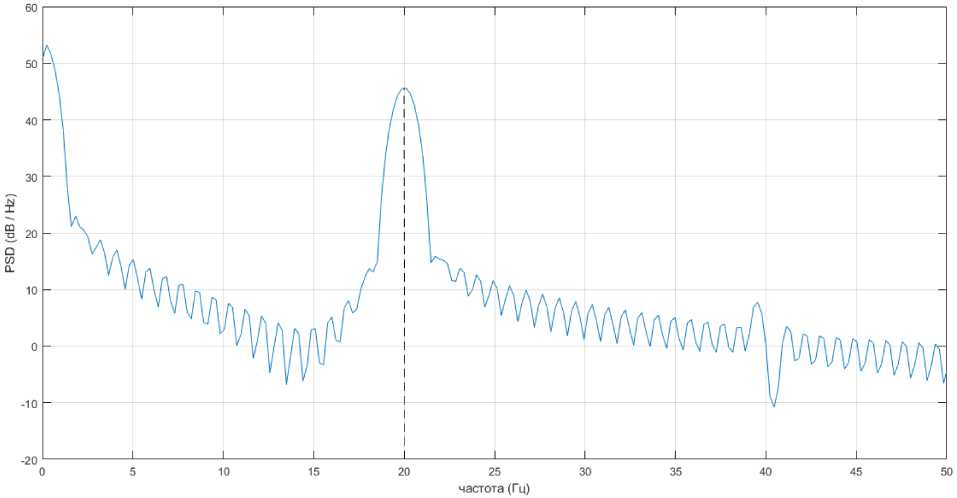
Рис. 6. Поиск огибающей частоты методом Уэлча

Fig. 6. Finding the frequency envelope using the Welch method

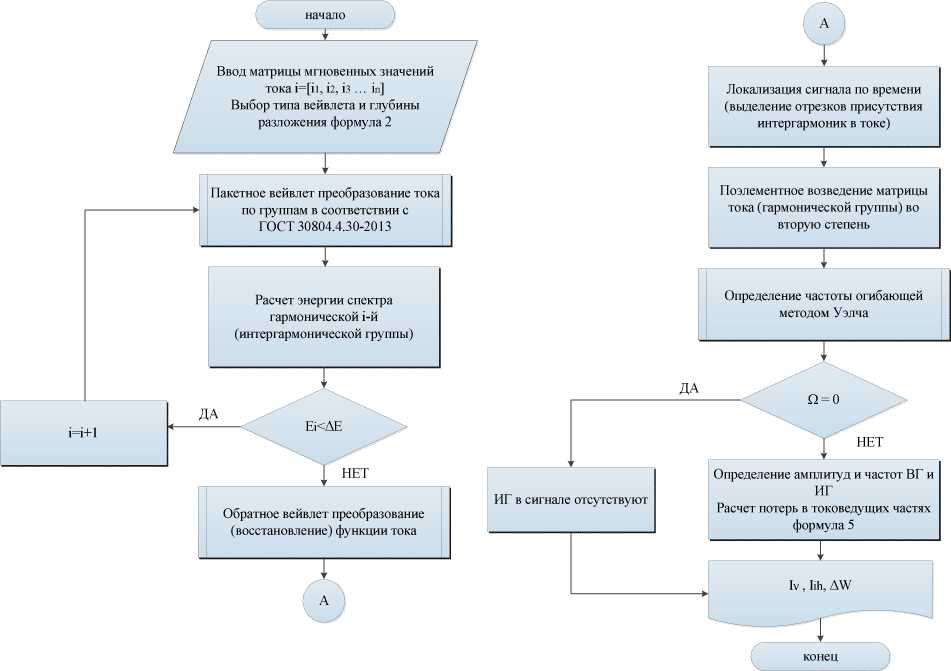
Рис. 7. Предлагаемый алгоритм Fig. 7. The proposed algorithm

Результаты численного эксперимента Numerical experiment results

f , Гц	50	130	150	230	250	350	370	450	470
I m , А	85,685	14,985	18,23	8,89	17,94	11,927	8,87	7,47	4,48
£ , %	0,02	0,1	1,27	3,42	0,33	0,61	2,64	0,4	0,44
A P , кВт	4,23	0,13	0,19	0,05	0,19	0,08	0,05	0,03	0,01