Алгоритм расчета рисковой стоимости инвестиционного портфеля

Инвестиционная деятельность сопровождается различными видами риска, которые имеют различную природу и оказывают различное влияние на итоговый результат. Интегральным показателем риска может выступать величина VаR.

Value at Risk (VaR) – стоимостная мера риска, выраженная в денежных единицах оценка величины, которую не превысят ожидаемые в течение данного периода времени потери с заданной вероятностью.

VaR характеризуется тремя параметрами:

• -    временным горизонтом , который зависит от рассматриваемой ситуации. По базельским документам – 10 дней, по методике «RiskMetrics» – 1 день. Чаще распространен расчет с временным горизонтом 1 день. 10 дней используется для расчета величины капитала, покрывающего возможные убытки;

• -    доверительным интервалом (confidence level) – уровнем допустимого риска. По базельским документам используется величина 0,99, в системе «RiskMetrics» – 0,95. Другие методики допускают 0,90 и 0,975;

• -    базовой валютой , в которой измеряется показатель.

VaR – это величина убытков, которая с вероятностью, равной уровню доверия (например, 0,99), не будет превышена. Следовательно, в 1% случаев убыток составит величину, большую, чем VaR.

Расчет величины VaR основан на процедуре моделирования и прогнозирования поведения стохастического показателя (случайной цены финансового инструмента на рынке ценных бумаг, банковского актива, выручки торговой организации и др.). В зависимости от характера временной зависимости стохастического показате- ля (трендовая, сезонная, тренд-сезонная, стационарная и т.д.) прогнозирование осуществляется с помощью различных моделей: экстраполяционных линейной парной и множественной регрессии, адаптивных Брауна и Хольта-Уинтерса, авторегрессионной и др.

В результате моделирования и прогнозирования получают традиционный результат: ожидаемая ве л ичина прогнозируемого показателя составит Y , а ввиду его стохастической природы диапазон возможных отклонений в большую и меньшую стороны будет определяться нижней Y н^пи^рж^{о г}н^{н оз} и Y в^пе^рр х^{о г н оз} верхней границами. Размах граничных значений определяется волатильностью показателя, временным горизонтом прогноза, а также задаваемой доверительной вероятностью попадания в прогнозный интервал.

Более простой подход основан на расчете только величины доверительн о го интервала, а в качестве оценки показателя Y выбирается его текущее значение. Этот подход оправдан в случаях, когда стоимость актива изменяет свое значение за счет незначительных случайных флуктуаций. В случаях сезонных колебаний или трендовой зависимости оценку показателя следует прогнозировать с учетом характера закономерностей. На практике при расчете VaR временной горизонт сост а вляет 1–10 дней, поэтому оценку показателя Y заменяет текущее значение при отсутствии сильных изломов тенденций и скачков стоимости.

Исходное выражение для расчета значения VaR имеет вид:

Var = - V • ( - m + к н • с т),       (1)

где V – текущая стоимость актива, m – ожидаемая (средняя) величина доходности, kН – квантиль нормального распределения (для вероятности 0,95 попадания в прогнозный интервал он составляет 1,645),

σ – стандартное отклонение доходности актива.

При расчете VaR с помощью формулы (1) предполагается, что случайная величина доходности m распределена относительно своего ожидаемого (среднего) значения нормально. Более точный подход требует установления вида функции плотности вероятности или функции вероятности (особенно это касается производных финансовых инструментов).

Для иллюстрации порядка расчета VaR рассмотрим портфель, состоящий из трех акций. Структура портфеля определяется путем решения оптимизационной задачи нелинейного математического программирования, в которой учи- тываются предпочтения инвестора: минимизация риска, максимизация доходности при приемлемом уровне риска, достижение наилучшего соотношения доходность-риск и др. В настоящей работе используется классическая модель Марковица для определения оптимальной структуры портфеля. Допустим, что начальный инвестиционный капитал позволяет приобрести такой портфель. Текущие котировки акций могут быть получены с помощью различных электронных ресурсов, например http://stocks. investfunds. ru/. Расчет проведем на один день с вероятностью 0,99 (требования базельской методики). Исходные данные в виде котировок цен ask и bid в рублях взяты на Московской межбанковской валютной бирже за десятидневный период 9–22 сентября 2009 г. и приведены в таблице 1.

Таблица 1

Котировки цен трех активов, входящих в портфель (цены в рублях)

№ п/п	Дата	«Газпром»	«Лукойл»	«Сургнг»	«Газпром»	«Лукойл»	«Сургнг»
		Bid, закр.			Ask, закр.
1	09.09.2009	170,31	1660	26,505	170,36	1660,1	26,51
2	10.09.2009	172,8	1660	26,29	172,99	1660,05	26,32
3	11.09.2009	173,95	1666,5	26,601	174	1666,99	26,697
4	14.09.2009	172,3	1653,03	27,205	172,38	1653,93	27,24
5	15.09.2009	176,6	1694	28,003	176,61	1696,8	28,049
6	16.09.2009	181,99	1690,02	27,852	182	1693	27,888
7	17.09.2009	181,15	1654,01	27,105	181,48	1657,98	27,147
8	18.09.2009	182,35	1670,01	27,501	182,45	1671	27,659
9	21.09.2009	175,97	1614	26,081	176	1615	26,143
10	22.09.2009	183,3	1648,1	26,251	183,4	1649,99	26,266
Среднее значение		177,07	1660,97	26,94	177,17	1662,48	26,99

Динамика цен акций представляется графически (в качестве примера на рис. 1 представлена динамика акций АО «Газпром»). Эти динамики имеют тенденцию изменения, и ожидаемые стоимости акций следует оценить с использованием, например, трендовой модели.

Линейные уравнения динамики цен акций (трендовые модели) имеют вид:

V Газпром = 1,2912 - t + 169,97, рас

• V//_C^K^ = - 2,5 - 1 + 1674,7, рас

• V C”^ = 0,002 - t + 26,93. р а с

Из уравнений видно, что цены акций «Газпром» и «Лукойл» имеют тенденцию изменения, следовательно, их ожидаемую стоимость следует оценить с использованием полученных моделей. Расчет на следующий, 11-й день (23.09.2009), дает:

V_rn = 1,2912 - 11 + 169,97 = 184,17 руб .,

• V„_x = - 2,5 - 11 + 1674,7 = 1647,20 руб .

Лк

Для акции «Сургутнефтегаз» коэффициент наклона линейной модели динамики цены близок к нулю, что свидетельствует об отсутствии тренда за последние 10 дней, и в качестве определения его цены следует рассматривать среднее значение за период, которое составит 26,94 руб.

Значение риска портфеля будет определяться суммой дисперсий отдельных активов с учетом их долей в портфеле, причем для первых двух акций целесообразно рассчитывать сред- а для акции «Сургутнефтегаз» – стандартное неквадратическое отклонение от линии тренда, отклонение.

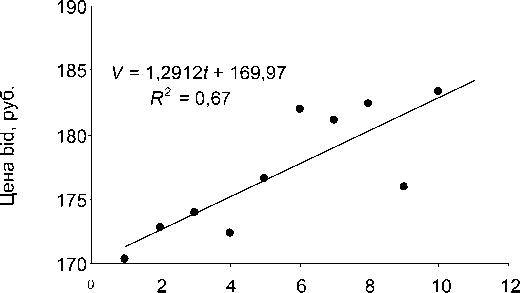
Время, дни

Рис. 1. Динамика цены акции АО «Газпром» за 9–22 сентября 2009 г.

Для решения задачи оптимального портфеля (формирования портфеля минимального риска и требуемой доходности) необходимо провести предварительные расчеты по определению ожидаемых доходностей и рисков отдельных активов, а также установить корреляционную матрицу взаимосвязи доходностей отдельных активов. Следует отметить, что инвестор уже имеет портфель, для которого оценивается VaR, т.е. имеются доли активов в портфеле, испо л ьзуемые для расчета V (текущей стоимости) и m (ожидаемой доходности). Поэтому приводимые ниже расчеты имеют дополнительный, иллюстративный характер. Текущая доходность k -го финансового инструмента, входящего в портфель, в течение рассматриваемого периода (9 июня–22 сентября 2009 г.) определяется соотношением:

• VL. - V^k,

Bid,t       Ask,o m k,t =---—k--100%,       (2)

VAsk,o где V Aksk , o – рыночная цена продажи k-го инструмента в день, соответствующий началу периода (9 сентября 2009 г.),

V _B^k_{id t} – рыночная цена покупки в день t определения доходности инструмента. Очевидно, что доходность существенно зависит от цены V _A ^k _{sk , o} .

Т.е. покупку инструмента (открытие позиции) следует осуществлять, когда цена V _A ^k _{s k , o} принимает небольшое значение за счет моментных колебаний цен.

Текущие значения доходностей и исходные данные для расчета структуры портфеля приведены в таблицах 2, 3.

Таблица 2

Исходные данные для расчета структуры портфеля и его рисковой стоимости

№ п/п	Дата	Доходность – m, %
		«Газпром»	«Лукойл»	«Сургнг»
1	09.09.2009	–0,0293	–0,006	–0,0189
2	10.09.2009	1,43226	–0,006	–0,8299
3	11.09.2009	2,1073	0,38552	0,34327
4	14.09.2009	1,13876	–0,4259	2,62165
5	15.09.2009	3,66283	2,04205	5,63184
6	16.09.2009	6,82672	1,8023	5,06224
7	17.09.2009	6,33365	–0,3668	2,24444
8	18.09.2009	7,03804	0,59695	3,73821
9	21.09.2009	3,29303	–2,7769	–1,6183
10	22.09.2009	7,59568	–0,7228	–0,977
Среднее значение		3,94	0,05	1,62
СКО ( σ ), %		2,80	1,35	2,61

Таблица 3

Компания	«Газпром»	«Лукойл»	«Сургнг»
«Газпром»	1
«Лукойл»	0,155	1
«Сургнг»	0,329	0,800	1

Матрица корреляций доходностей акций

Математическая модель Марковица формирования оптимального портфеля в общем виде может быть представлена в виде системы ограничений и неравенств, представляющих собой задачу нелинейного математического программирования. Величина риска портфеля определяется с учетом попарных корреляций и рисков отдельных активов, выраженных в виде среднеквадратических отклонений. Общая постановка задачи Марковица оптимального портфеля минимального риска запишется с учетом ограничений в виде:

° p = Z Z x i " Xj " ° i " ° j " corm ; m j 1 ^ min

V i = 1 j = 1

mp = ZLm- ■ x - mo, i =1

n

Z Xi= 1, i=1

xi - 0, i = 1, n.

В качестве величины безрискового актива m _o выбрано значение 3%, которое находится в диапазоне от минимальной до максимальной доходности отдельных активов портфеля.

Для рассматриваемого случая экономикоматематическая модель с учетом данных таблиц 2 и 3 запишется в виде:

<

° _p = ^2,8 2 ■ x 2 + 1,35 2 ■ x 2 + 2,61 2 ■ x ₃ ² + 2 ■ x 1 ■ x ₂ ■ 2,8 ■ 1,35 ■ 0,155 + + 2 ■ x 1 ■ x ₃ ■ 2,8 ■ 2,61 ■ 0,329 + 2 ■ x ₂ ■ x ₃ ■ 1,35 ■ 2,61 ■ 0,8 ^ min m_n = 3,94 ■ x . + 0,05 ■ x ₇ + 1,62 ■ x ₃ - 3

p   1   23

x 1 + x ₂ + x ₃ = 1

x 1 - 0, x ₂ - 0, x ₃ - 0

Решение задачи (3) осуществляется с помощью специальных численных методов. Реализация одного их таких методов представлена в виде надстройки MS Excel «Поиск решения».

Оптимальным решением задачи (3) будет вектор x * = 0,706, x * = 0,1642, x * = 0,1298, при котором ожидаемая доходность портфеля составит m = 3% , а риск ° _p = 2,186% .

Прогнозная стоимость портфеля на 23 сентября 2009 г. определяется ожидаемой стоимостью отдельных активов, имеющих соответствующие доли:

V_p = 184,17 ■ 0,706 + 1647,20 ■ 0,1642 +

+ 26,94 ■ 0,1298 = 403,88 руб .

Из формулы (1) для доверительной вероятности 0,99 ( k _Н = 2,326) определим значение VaR на следующий день (23 сентября 2009 г.):

VaR = - 403,88 ■ ( - 0,03 +

+ 2,326 ■ 0,0219) = - 8,43 руб .

Фактическая стоимость портфеля по состоянию на 22 сентября 2009 г. составила:

V _p (22.09) = 183,3 ■ 0,706 + 1648,10 ■ 0,1642 +

+ 26,251 ■ 0,1298 = 403,42 руб .

Можно утверждать, что с вероятностью 0,99 потери по портфелю стоимостью 403,42 руб. (по состоянию на 22 сентября 2009 г.), состоящему из акций «Газпром», «Лукойл», «Сургутнефтегаз» в соотношении соответственно 0,706– 0,1642–0,1298 на следующий день (23 сентября 2009 г.) не превысят 8,43 руб. Относительные потери могут составить

⁸’⁴/4₀₃,4₂ ^ ¹⁰⁰ = ^2J%.

Для оценки точности предложенного метода следует определить фактическое значение разницы стоимости портфеля на 23 сентября 2009 г. и на 22 сентября 2009 г., с тем чтобы сравнить ее с расчетным значением VaR. С учетом котировок акций на 23 сентября 2009 г. фактическая текущая стоимость составила:

V p = 180,01 - 0,706 + 1608,72 - 0,1643 +

+ 25,581 - 0,1298 = 394,68 руб .

Разница фактических значений стоимостей портфеля 394,68 – 403,42 = –8,88 руб. Расчетное значение VaR равное 8,43 руб. отличается от фактической разницы 8,88 руб. на

(8,88 — 8Л%88 - 100 = 5,1%, что свидетельствует о высокой относительной точности предложенной методики.

В рассматриваемом примере изменение цен акций портфеля только за один день (с 22 по 23 сентября 2009 г.) составило:

(180,01 -

183,3)

183,3

- 1,79%

для акций «Газпром»,

(1608,72 - 1648,1)/    .100--2 34%

/1648,1 100 = 2,34 % для акций «Лукойл»,

(25,581 - 26,251)/

26,251

- 100 = - 2,55%

для акций «Сургутнефтегаз».

Заниженное расчетное значение VaR по сравнению с фактической разницей стоимостей портфеля связано с высокой волатильностью россий-ского рынка ценных бумаг и допущением нормальности распределения случайных значений доходностей акций. Это может быть скорректировано величиной доверительной вероятности. Например, выбирать значение 0,995, для которого квантиль нормального распределения составляет 2,58, а значение VaR окажется равным –10,62 руб., что превышает наблюдаемое снижение стоимости портфеля на 8,88 руб.

Предложенный алгоритм определения величины VaR портфеля апробирован путем анализа реальных котировок акций, по которым сформирован оптимальный портфель. Удовлетворительное совпадение результатов расчета с фактическими данными позволяет сделать вывод о возможности использования данного подхода при оценке инвестиционных рисков.

Рассчитанная по предложенному алгоритму рисковая стоимость на практике позволяет вносить коррективы в принимаемые управленческие решения в области финансового планирования, а также оценивать величину возможных убытков.