Алгоритм распознавания космических объектов на основе нейронных нечетких сетей с использованием интеграции информации от различных средств наблюдения

Необходимость контроля и мониторинга околоземного космического пространства (ОКП) обусловлена важными военными [8] и народно-хозяйственными целями [9]. Одной из важнейших задач систем мониторинга ОКП является задача распознавания космических объектов, включающая в себя подзадачи классификации космических объектов (КО) по типу (пилотируемый космический аппарат, ракета-носитель, элементы запуска или функционирования КО, фрагмент разрушения и т.д.) и его идентификации (государственной принадлежности, целевого назначения, степени опасности, функционального состояния и т.д.) [10]. Своевременное обнаружение искусственных спутников земли, представляющих опасность для своей страны, определение национальной принадлежности таких КО, их функционального состояния и других характеристик, повысят безопасность космических полетов, а также обеспечат сохранность благополучной экологической и политической обстановки [11].

Существующие методики распознавания не в полной мере могут обеспечить достаточную оперативность классификации и идентификации космических объектов с надлежащей точностью [12]. Предлагаемая методика основана на применении комбинированных искусственных нейронных сетей и интеграции информации о космических объектах из различных источников [13].

4 в ыпуск 4/2020

Распознаванием и сопровождением информации о космических объектах занимается система контроля космического пространства (СККП), включающая в себя оптико-электронные, радиолокационные и лазерно-оптические средства распознавания, ряд гражданских организаций, таких как Пущинская радиоастрономическая обсерватория Астрокосмического центра ФИАН им. Лебедева, Институт прикладной математики имени Келдыша РАН и др. [4]. При этом возникает проблема разнородности и неполноты информации о КО, которая связана с необходимостью обработки большого объема зачастую повторяющейся и противоречивой информации о космических объектах из различных источников [14].

Решением этой задачи может стать применение нечетких нейронных сетей с применением технологии интеграции данных из различных источников [15]. Обучив нейронную сеть соотносить разнородную информацию, такую как параметры блеска КО, лазерно-оптические и радиолокационные параметры, дополняя, таким образом, недостающие параметры, можно увеличить количественные и качественные показатели информации [16]. При увеличении объема информации может иметь место ее дублирование, в связи с этим при росте количественных показателей могут падать качественные. Для повышения качества необходимо исключить дублирование данных [17].

Использование нечетких множеств необходимо для описания неоднозначно понимаемых событий, объектов и понятий. Для оценки и классификации объектов, описываемых нечеткими множествами, используется понятие меры неопределенности. Свойства, которым должен удовлетворять такой показатель, называемый показателем размытости (или мерой энтропии) нечетких множеств, и в качестве этого показателя был предложен функционал, аналогичный шенноновской энтропии в теории информации [5]. В настоящее время рассматриваются различные альтернативные подходы к определению показателя размытости нечеткого множества, обсуждаются его свойства и возможные приложения.

Модель распознавания КО на основе нечетких нейронных сетей

В общем случае космические объекты в различные моменты времени с определенной долей вероятности находятся в той или иной точке в пространстве. Если задавать характеристики и стратегии движения КО в виде интервалов возможных значений, результатом будет множество параметров движения и маневров. Следует учитывать и тот факт, что от длительного пребывания в космическом пространстве меняются механические, оптические и другие свойства материалов космических аппаратов, что с течением времени может повлиять на точность распознавания КО.

В связи с этим предлагается использовать математический аппарат нечетких искусственных нейронных сетей. Преимущества использования нейросетей заключаются в следующем [1].

• 1.    Свойство ассоциативности, позволяющее обрабатывать множество КО и оперировать образами ситуаций моделирования, а не их отдельными описаниями.

• 2.    Способность к обучению, которая дает возможность получать устойчивые решения по результатам имитационного моделирования прикладных задач в реальном масштабе времени.

Зимовец А.И. Алгоритм распознавания космических объектов...    5

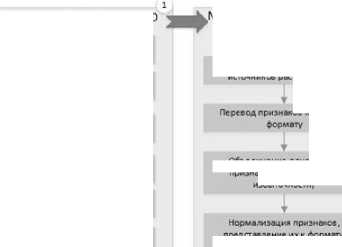
Для решения поставленной задачи предлагается модульная модель нейронной сети, представленная на рисунке 1, где:

• •    модуль 1 представляет собой совокупность средств распознавания различной направленности (оптико-электронные, радиолокационные, лазерно-оптические средства);

• •    модуль 2 отвечает за предварительную обработку признаков распознавания, в котором производится интеграция данных, перевод признаков распознавания в единый формат, избавление от избыточности и нормализация признаков для дальнейшего анализа;

• •    модуль 3 отвечает за анализ различных признаков распознавания;

• •    модуль 4 отвечает за формирование характеристик по итогам работы предыдущего модуля и вывод отчета о распознавании.

  Модуль предварительной обработки признаков распознавания

  Интеграция информации из всех истокнивсв распознавания

  

  представление их к формату, необходимому для анализа

  
  
  
  
  

  перевод признака» к единому

  
  

  Объединение однотипных признеки (избавление от избыточности)

  
  
  

  Модуль анализа признаков распознавания

  
  

  Диагностика по признаку * Высота орбиты»

  
  

  Диагностика по признаку «Форма КО»

  
  

  Диагностика по признаку * Координатные признаки»

  
  
  

  Модуль формирования

  
  

  Формирование вектора вторичных характеристик по резу а, тагах* работы предыдущего модуля

  
  

  Вывод общего вектора характеристик

  
  

Рис. 1. Модель искусственной нейронной сети для распознавания КО

На рисунке 2 представлен многослойный перцептрон, состоящий из входного слоя, трех скрытых слоев и выходного слоя.

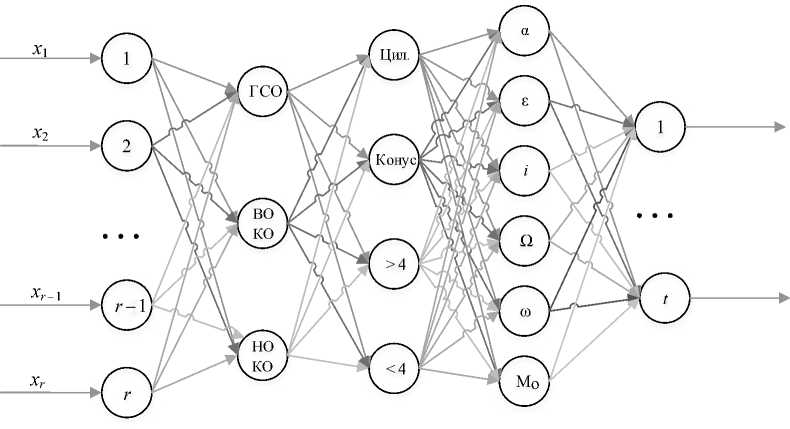
Рис. 2. Многослойный перцептрон для распознавания КО

6 в ыпуск 4/2020

Составные нечеткие высказывания объединяются в правила с помощью нечеткой логической операции конъюнкции (И) или дизъюнкции (ИЛИ). Входные характеристики имеют терм-множество {«высокий», «средний», «низкий»}. В таблице 1 приводится база правил для алгоритмов нечеткого вывода Мамдани, Ларсена и Такаги – Сугено [10].

Таблица 1

База правил для алгоритмов нечеткого вывода Мамдани, Ларсена и Такаги – Сугено

№ правила	Общие условия всех алгоритмов	Заключения для алгоритмов
		Мамдани и Ларсена	Такаги – Сугено
1	ЕСЛИ z есть X 1 И q есть A 1	ТО y есть F 1 (низкая)	y = a 1 z + b 1 q
2	ЕСЛИ z есть X 1 И q есть A 2	ТО y есть F 2 (средняя)	y = a 2 z + b 2 q
3	ЕСЛИ z есть X 2 И q есть A 1	ТО y есть F 2 (средняя)	y = a 2 z + b 2 q
4	ЕСЛИ z есть X 2 И q есть A 2	ТО y есть F 3 (высокая)	y = a 3 z + b 3 q
5	ЕСЛИ z есть X 3	ТО y есть F 3 (высокая)	y = a 3 z + b 3 q

Входная переменная X описывается тремя функциями принадлежности X_i , а A – двумя функциями принадлежности A_i , выходная переменная F описывается тремя функциями принадлежности F_i . В базе правил нельзя разместить больше вариантов правил, чем произведение числа функций принадлежности всех входных переменных. Их число равно 6 (2 × 3). Максимальное количество правил в базе определяется соотношением l = l ₁ ∙ l ₂ ∙ … ∙ l_m , где l_i – коли чес тво функций принадлежности, используемых для задания входной переменной x i ( i = 1, m ) .

Сравнение алгоритмов

Предположим, что распознаваемый космический объект определяется четырьмя основными характеристиками x ₁, x ₂, x ₃ и x ₄ (долгота восходящего угла, наклонение, большая полуось и перицентр), представленными в виде лингвистических переменных. Тогда база правил будет состоять из двух правил с четырьмя входами и одним выходом. Для упрощения расчетов область определения нормируется каждой из характеристик в интервал [1, 10]. При определении классификации космического объекта ограничимся категориями «пилотируемый летательный аппарат», «спутник навигации», «спутник связи», «метеорологический спутник».

Алгоритм Мамдани предложен одним из первых и описывается следующим образом:

Правило 1: ЕСЛИ x ₁ есть А ₁₁ И x ₂ есть А ₁₂ И x ₃ есть А ₁₃ И x ₄ есть А ₁₄ ТО y есть B ₁.

Правило 2: ЕСЛИ x ₁ есть А ₂₁ И x ₂ есть А ₂₂И x ₃ есть А ₂₃ И x ₄ есть А ₂₄ ТО y есть B ₂.

Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Правила, степень истинности условий которых отлична от нуля, считаются активными.

Активизация подзаключений в нечетких правилах продукций выполняется с помощью min-активизации по формуле (1), причем для сокращения времени вывода учитываются только активные правила:

µ′( y ) = min{ c_i , µ( y )}, (1) где C = { c ₁, c ₂, …, c_q } – множество степеней истинности; q – общее количество подзаключений в базе правил.

Зимовец А.И. Алгоритм распознавания космических объектов...

На рисунке 3 представлен пример построения функции принадлежности.

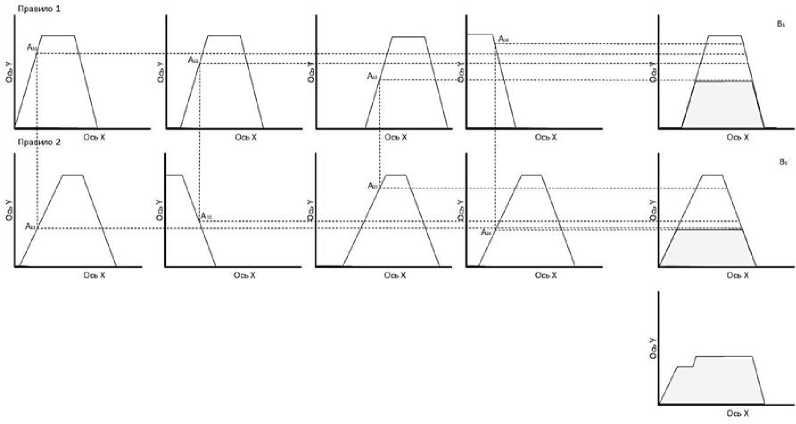
Рис. 3. Построение функции принадлежности

В базе правил для алгоритма Такаги – Сугено используются правила нечетких продукций в следующей форме:

Правило 1: ЕСЛИ x ₁ есть А ₁₁ И x ₂ есть А ₁₂И х ₃ есть А ₁₃ И х₄ есть А ₁₄

ТО y = c ₁₁ x ₁ + c ₁₂ x ₂ + с ₁₃ х ₃ + с ₁₄ х ₄ + с ₁₀.

Правило 2: ЕСЛИ x ₁ есть А ₂₁ И x ₂ есть А ₂₂ И х ₃ есть А ₂₃ И х ₄ есть А ₂₄

ТО y = c ₂₁ x ₁ + c ₂₂ x ₂ + с ₂₃ х ₃ + с ₂₄ х ₄ + с ₂₀.

Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min-конъюнкции:

α1 = min {µ A ₁₁( x ₁’), µ A ₁₂( x ₂’), µ А ₁₃( х ₃’), µ A ₁₄( x ₄’)},

α2 = min {µ A ₂₁( x ₁’), µ A ₂₂( x ₂’), µ A ₂₃( x ₃’), µ A ₂₄( x ₄’)}.

Для выполнения агрегирования могут использоваться и другие логические операции. Правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

Активизация подзаключений в нечетких правилах продукций

Во-первых, с использованием min-активизации, как и в алгоритме Мамдани, находятся значения степеней истинности всех заключений правил нечетких продукций. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила. Это выполняется с использованием формул для заключения:

’’’ y1      11 1     12 2     13 3     14 410

’’’ y2     21 1     22 2     23 3     24 420

Здесь вместо x ₁ и x ₂ подставляются значения входных переменных до этапа фаз-зификации.

8   в ыпуск 4/2020

Аккумуляция заключений нечетких правил продукций фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами у _j .

При дефаззификации выходных переменных используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств:

y’ = (α1 y1’+ α2 y2’) / (α1 + α2), при этом не требуется проведение предварительного аккумулирования активизированных заключений отдельных правил.

Сравнительный анализ алгоритмов Мамдани – Ларсена и Такаги – Сугено представлен в таблице 2.

Таблица 2

Сравнительный анализ алгоритмов

№	z i	qi	Выходные значения нечеткой продукционной модели				M
			Мамдани		Такаги – Сугено
			Y М	Δ M	Y T–C	Δ T–C
1	0,22	4	0,216	29,3	0,076	54,5	0,167
2	0,71	1	0,71	14,8	0,631	24,2	0,833
3	0,34	2	0,457	8,6	0,205	59	0,5

Анализ показывает, что наименьшее отклонение от средних выходных значений показал алгоритм Мамдани (от 8,6 до 29,3%), наименьшую точность показал алгоритм Такаги – Сугено (отклонение от 24,2 до 59%). Также в качестве недостатка алгоритма Такаги – Сугено нужно отметить сложность формирования экспертами заключений по каждому правилу.

Заключение

В статье рассмотрены задачи, поставленные перед системой контроля космического пространства, представлены модель распознавания космических объектов и структура нечеткой нейронной сети, предложенной для решения поставленной задачи. Проведено сравнение алгоритмов нечеткого вывода, представлены базы правил и пример построения функции принадлежности.