Алгоритм разделения ячеек для планирования пути манипуляционного робота

В [12] описан алгоритм создания карты и планирования пути для автономного мобильного робота в неизвестной статической среде. Робот изучает среду с помощью вероятностной интерпретации, основанной на видеосенсорах, видимых углов и границ. Робот перемещается в пространстве, ориентируясь на основе визуального сходства, т. е. ассоциативно. Для построения ассоциативной памяти применяется нейронная сеть. Робот получает от видеокамеры изображение, которое поступает в виде вектора на входной слой нейронной сети, с помощью которой текущее изображение сравнивается с уже имеющимися изображениями и вставляется в сегмент с наиболее похожими. Таким образом, среда может быть изучена и представлена, как серия визуально различных местоположений. Топология среды строится роботом во время планирования пути путем выявления общих свойств у известных местоположений. Данный алгоритм планирования подходит для двухмерного пространства состояний. В [8] представлен алгоритм планирования локального пути для мобильного робота с видеосен-сорной системой и метод трансформации двумерных изображений в трехмерную модель. Задача решается в три этапа. На первом этапе детекторы обнаруживают препятствия. На втором этапе двумерное изображение препятствий трансформируется в трехмерную модель, и на третьем – планируется локальный путь при помощи алгоритма фронта распространения волны, избегающий столкновения с этими препятствиями. В [14] представлен алгоритм планирования пути мобильного робота в неизвестной среде. На пространство накладывается двумерная сетка, затем датчики робота определяют, в какой из ячеек сетки находятся препятствия, т. е. строится следующая модель пространства – ячейкам присваиваются различные значения в зависимости от того, есть ли в них препятствия или нет, или через сколько времени препятствие прибудет в эту ячейку. После чего планирование пути по сетке пространства осуществляется при помощи генетического алгоритма.

Планирование пути манипулятора усложняется многозвенностью манипуляторов, в [4] разработан метод, подходящий для планирования пути избыточных и гиперизбыточных манипуляторов: BB-метод (BB-method). Путь без столкновений с препятствиями находится с помощью постепенных изменений первоначального пути, который обычно является прямой, связывающей начальное и целевое положения. Сложность алгоритма зависит линейно от степеней свободы робота. ВВ-метод не гарантирует достижения цели. В [5] представлен метод планирования в неизвестной среде: utility-guided planning («полезноуправляемое планирование»). Планирование utility-guided – итеративный подход, который начинается «без знания мира» и постепенно строит некоторую аппроксимацию окружающей среды, модель, удобную для планирования. Представленный подход может использоваться как фрейм для методов планирования, и подходит для динамической среды.

Сформулируем требования к методу управления манипулятором в неизвестной среде: метод должен гарантировать достижение цели, подходить для использования видеосенсорной системы, применяться для n -звенных манипуляторов, иметь возможность встраивания различных алгоритмов планирования пути в областях, где препятствия известны. АНС удовлетворяет данным требованиям [2]. Планирование движения динамической системы в пространстве состояний при неизвестных запрещенных состояниях сводится к решению конечного числа задач планирования в пространстве с известными запрещенными состояниями [1; 11].

В АНС информация о запрещенных состояниях поступает по мере движения робота и в связи с этим образуются зоны свободных и запрещенных точек. Таким образом, возникает потребность планирования пути в среде с известными запрещенными состояниями, используя информацию об этих зонах. Наилучшим образом для этой цели подходят алгоритмы разделения ячеек. Так как с помощью алгоритмов разделения ячеек планирование происходит по свободным областям, получается, что основной единицей вычислений в алгоритме является множество точек, это позволит сократить время планирования пути и при реализации алгоритма сократить объем вычислительных ресурсов.

Различные виды алгоритмов точного разделения ячеек представлены в [10; 13]. Вертикальное разделение ячеек или трапециевидная декомпозиция для двумерного и трехмерного пространства, описана в [6; 7; 9; 10; 13], в [10] так же указано, что метод может быть усовершенствован для применения в n -мерном пространстве. Однако препятствия должны быть кусочно-линейными, т. е. должны быть представлены как полуалгебраическая модель [10], для которой все примитивы являются линейными. К сожалению, в большинстве задач планирования движения возникают нелинейные алгебраические примитивы из-за нелинейных преобразований, которые появляются в результате вращений форм.

Метод триангуляции пространства для двумерного пространства, описанный в [6; 7; 10], заключается в представлении свободного пространства в виде сим-плициального комплекса. Алгоритм триангуляции очень сложен и затрачивает много времени на исполнение.

Цилиндрическая декомпозиция [10] похожа на вертикальное разделение ячеек, за исключением того, что границы разделения ячеек не останавливаются на границах препятствий, а расходятся в бесконечность. Получаем точки, которые принадлежат как свободному пространству, так и препятствиям. Для окончательного описания границ ячеек используются логические предикаты. От цилиндрической декомпозиции легко перейти к любой размерности пространства, топологии пространства конфигураций и полуалгеб-раическим моделям. Цилиндрическая алгебраическая декомпозиция решает любую задачу планирования движения. Однако определение смежности ячеек для данного метода является трудной задачей. Время работы цилиндрической алгебраической декомпозиции зависит от многих факторов, но основное влияние на длительность оказывает количество полиномов в модели.

Также в [13] представлены декомпозиция бустро-федон ( boustrophedon decomposition ), для усовершенствования данного метода – декомпозиция Морзе и декомпозиция, основанная на видимости ( Visibilitybased decomposition ), которые применяются в двумерном пространстве.

Существуют методы аппроксимирующей декомпозиции [9]. В них также свободное пространство представлено в виде множества ячеек, но ячейки имеют простую заданную форму, например прямоугольники.

Большинство работ рассматривают алгоритмы разделения ячеек для двумерного пространства [10; 13], такие алгоритмы больше направлены на генерацию пути для мобильных роботов, и не удовлетворяют поставленным задачам в управлении манипуляторами, имеющими более двух степеней подвижности.

Ниже предлагается версия алгоритма разделения ячеек (АРЯ), подходящего для генерации пути движения n -звенного манипулятора, который объединяет разрешенные конфигурации манипулятора в «свободные области», сокращая этим время вычисления пути.

Алгоритм разделения ячеек. Полное описание алгоритма дано в [3]. Планирование в известной среде осуществляется в дискретизированном пространстве обобщенных координат. Ячейкой назовем множество точек дискретизированного пространства, находящихся на одной линии дискретизации и имеющих координаты ( x 1 , x 2 , …, x n ), где, например, x 1 , x 2 , … , x n- 1 имеют одинаковые значения для всех точек одной ячейки, а x n – различны. Хотя данный способ выделения ячеек не объединяет точки пространства в ячейки во всех измерениях, но даже такая декомпозиция позволит нам оперировать множеством точек одновременно и ускорить работу алгоритма планирования пути. Свободной областью называется множество смежных точек ячейки, не содержащих ни одной запрещенной точки.

Алгоритм имеет три этапа и вызывается из АНС каждый раз, когда возникает необходимость в планировании предварительного пути. Исходные данные: X ⁰ = qⁿ , X^T = q^T , Q (множество запрещенных точек, включая конструктивные ограничения), где qⁿ – текущая конфигурация манипулятора, точка смены пути [2].

Этап 1. Создание таблицы свободных областей TFR (table of free regions) на основе информации, переданной сенсорной системой при вызове подпрограммы планирования пути (используется множество Q), если она еще не создана. Если таблица TFR уже существует, то в нее вносятся изменения в соответствии с новой информацией, поступившей от сенсоров. В каждой ячейке может быть одна или более свободных областей, i-ая строка TFR соответствует i-ой ячейке, каждая свободная область этой ячейки характеризуется двумя крайними точками. По определению ячейки, компоненты координат точек, принадлежащих одной ячейке, одинаковы, кроме одной компоненты xn, значение этой компоненты и будет служить уникальным идентификатором каждой точки в одной ячейке. Так как в свободной области точки являются смежными, то для обозначения границ области достаточно указать идентификаторы двух крайних точек (табл. 1).

Этап 2. Построение графа поиска , который представляет собой дерево соединений свободных областей . Корнем дерева является свободная область, содержащая целевую конфигурацию Х^Т . Узел дерева имеет как входящие, так и исходящие ветви. Корень дерева – это узел, у которого только исходящие ветви. Лист дерева – это узел, у которого только входящие ветви. Значениями узлов дерева являются границы свободных областей ячеек. Лист присоединяется к узлу, если его свободная область соединима со свободной областью данного узла (определяется по TFR ) и если такого узла еще нет в дереве. Построение дерева прекращается, если листом дерева стала область, содержащая начальную конфигурацию Х ⁰. Для выбора следующего рассматриваемого листа использовался алгоритм поиска в глубину.

Этап 3. Строим путь, используя дерево соединения свободных областей, поднимаясь от последнего присоединенного листа, в котором указана свободная область, содержащая начальную точку X ⁰, к корню дерева, в котором содержится область с конечной конфигурацией X^T . Путь строится в 3 этапа:

• 3.1.    Строим последовательность базовых точек пути, выбирая по одной точке из каждой свободной области, через которые будет проходить путь, т. е. области, принадлежащие узлам дерева между последним узлом и корнем.

X ⁰ – первая точка последовательности базовых точек пути.

При построении базового пути используется уравнение прямой, проходящей через две точки на плоскости:

x - x i = У - У 1 x 2 - x i У 2 - У 1

Из формулы (1) получим

y = ylZyl. x 2 - x i

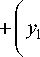
x i ■

У 2 ^- У 1 x 2 - x i .

Задавая абсциссу x точки, получаем y ( x ₁, y ₁) – координаты предыдущей точки базового пути, ( x 2 , y 2 ) – координаты целевой точки. Так как в ячейке все точки имеют одинаковые компоненты координат, кроме компоненты xⁿ , используем проекции предыдущей точки базового пути и целевой точки на плоскость Ox 1 x n как точки для прямой на плоскости и находим компоненту xⁿ . Для пути выбираем ближайшую к ( x , y ) разрешенную точку рассматриваемой свободной области.

• 3.2.    Добавляем точки в последовательность базовых точек пути, если между двумя точками расстояние больше одного шага дискретизации.

Просматриваем последовательность базовых точек и находим пару точек, расстояние между которыми больше одного шага дискретизации. Запишем координаты двух соседних точек последовательности в следующем виде (на примере трехмерного пространства):

111 222

( x ₁, x ₂, x ₃) AND ( x ₁, x ₂, x ₃). (3)

Если | x 3 - x ₃ ²| >  i, то расстояние между точками больше одного шага дискретизации. Добавим столько точек между ними, сколько необходимо. Найдем x ₃ первой точки между этими двумя точками:

если x 3 <  x 2 , то x ₃ = x 3 + i;

если же x 3 >  x 2 , то x ₃ = x 3 - 1.

Остальные компоненты координат берем, для начала, как у предыдущей точки. Проверяем, принадлежит ли новая точка той же свободной области, что и предыдущая точка последовательности базовых точек. Если точка не лежит в границах области, тогда компоненту х 3 новой точки оставляем той же, но оставшиеся компоненты координат берем, как у следующей точки, из последовательности базовых точек и т. д.

• 3.3.    Удаляем петли из пути , т. е. отрезки пути, которые выходят из какой-либо точки, а затем в нее же возвращаются или проходят в одном шаге дискретизации. Последовательно перебираем точки пути и для каждой точки ищем среди оставшихся точек последовательности точку, которая равна текущей или лежит в одном шаге дискретизации от текущей. Если такая точка найдена, то все точки от текущей до найденной, включая найденную точку, удаляются из пути.

После того как предварительный путь получен, управление возвращается АНС.

TFR

Таблица 1

№ ячейки	Количество свободных областей	Границы области 1	Границы области 2		Границы области M
1	1	x n (1) – x n ( k )
2	M	x n (i) - x n ( a i )	x n ( a 2) - x n ( a 3 )		x n ( a , ) - x n ( k )

Примечания : k – количество возможных различных значений компоненты x_n ; M < k – количество свободных областей в ячейке; a _i, a ₂, ^, a j e [ x n (i); x n ( k )] - какая-то компонента координат x n .

Программная реализация. На основе алгоритмов создано программное обеспечение управления манипулятором в среде с неизвестными препятствиями.

Задана рабочая сцена для тестирования (рис. 1 и 2).

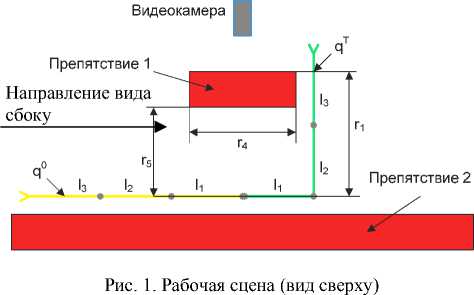
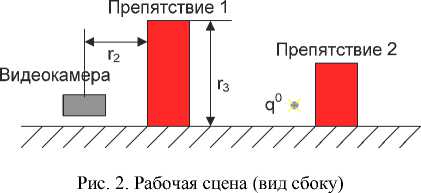
Видеокамера определяет расстояния r₂, r₃ и r₄ . Тестовая рабочая сцена удовлетворяет следующим соотношениям: 1 1 <  r₅, 1 2 <  r ₅, 1 3 <  r ₅, 1 2 + 1 3 >  r 1 , где l 1 , l 2 , l 3 – длины звеньев манипулятора.

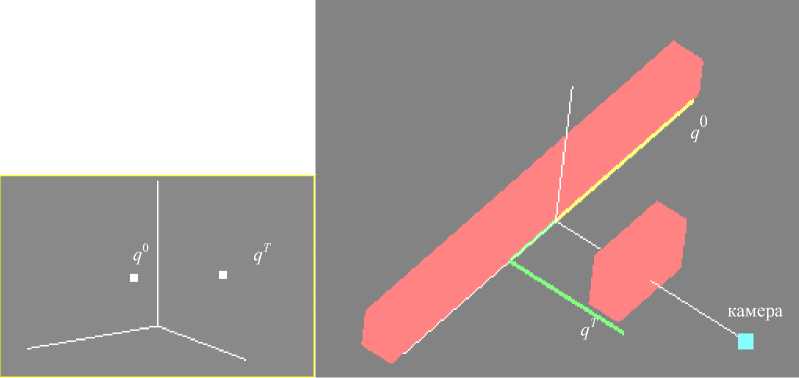
Начальная и целевая конфигурации (рис. 3) заданы оператором в виде векторов обобщенных координат: q0 = (3,14; 0; 0) радиан, qT = (0; 1,57; 0) радиан, шаг дискретизации равен 0,314 радиан, количество шагов дискретизации – 20. Оператором заданы также вектора ограничений, наложенные на звенья, вектор нижних значений XL = (0; –3,14; –3,14), вектор верхних значений XH = (6,28; 3,14; 3,14). Препятствия – два параллелепипеда темного цвета, размер и положение которых заданы оператором, но до начала движения подсистеме планирования пути о препятствиях ничего не известно. Роботу поставлена задача переместиться из конфигурации q0 в конфигурацию qT, qn= q0.

Перед началом планирования пути модуль имитации видеосенсорной системы обнаруживает некоторые препятствия в рабочей зоне. Камера (см. рис. 1 и 2), «видит» только ближайшую к камере грань малого препятствия. Модуль рассчитывает запрещенные конфигурации, которые пересекаются с данной гранью препятствия (см. рис. 3), облако точек – это полученные запрещенные конфигурации манипулятора (рис. 4).

После того, как информация, полученная от ви-деосенсорной системы, представлена в виде запрещенных конфигураций, алгоритм разделения ячеек генерирует предварительный путь, соединяющий X ⁰ и X^Т (где X ⁰ = qⁿ , X^T = q^T ), и возвращает управление АНС.

Конфигурации, которые принимал манипулятор во время движения, отражены на рис. 5 (темного цвета). Путь P состоит из 34 конфигураций, не включая начальную и конечную конфигурации, этот же путь представлен в пространстве обобщенных координат (рис. 6, точки темного цвета).

Путь P соединяет q ⁰ и q^T и является результатом объединения путей P i , созданных при каждом вызове подпрограммы планирования пути:

m

P = u P , (4)

i = 1

где m – количество вызовов алгоритма разделения ячеек.

б

а

Рис. 3. Стартовая q ⁰ и целевая q^T конфигурации ( а ), декартовое пространство ( б )

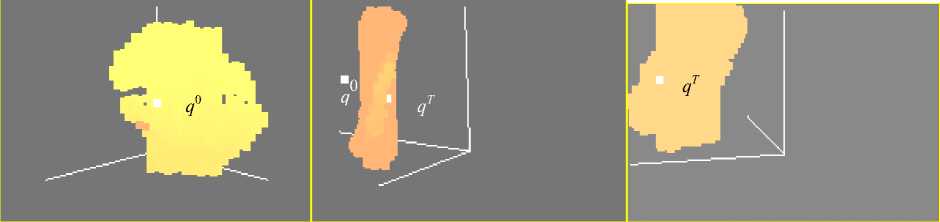
Рис. 4. Расчет запрещенных конфигураций манипулятора

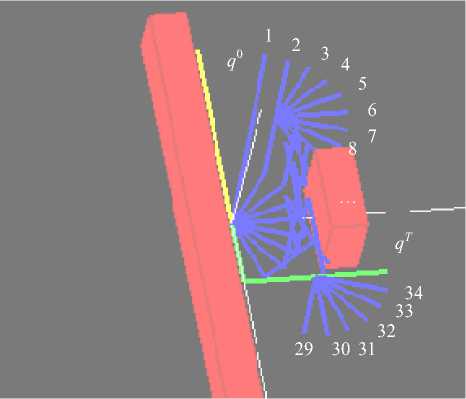
Рис. 5. Путь манипулятора

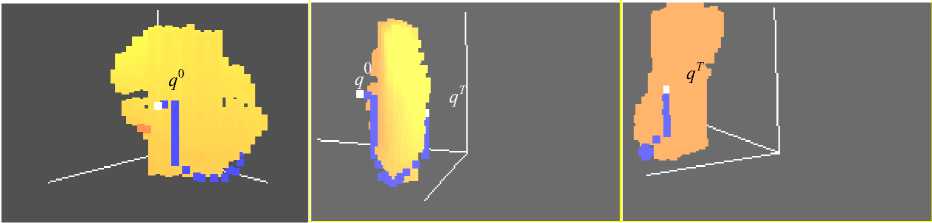
Рис. 6. Конфигурации пути в системе обобщенных координат

Сравнение времени работы в зависимости от типа сенсорной системы

Таблица 2

Количество шагов дискретизации	Не учитывая информацию от видеосенсоров		Учитывая информацию от видеосенсоров
	Время, с.	Количество вызовов	Время, с.	Количество вызовов
20	228	213	12	10

Данный путь P составлен из путей Pi (i = 1, 2, …, 10), сгенерированных в результате десяти вызовов подпрограммы планирования пути. Следовательно, в данном примере манипулятор 9 раз столкнулся с ранее неизвестным препятствием, которым являлась грань препятствия, невидимая для видеокамеры. Это препятствие манипулятор обнаружил имитацией тактильных датчиков.

В случае использования видеосенсорной системы, результат получить значительно быстрее (табл. 2).