Алгоритм реконструкции трёхмерной структуры кристалла по двумерным проекциям

На сегодняшний день большое внимание уделяется задаче реконструкции трёхмерных объектов по двумерным проекциям [1–4]. Существует два основных класса проекций: перспективные и параллельные. Перспективные проекции применяются зачастую для восстановления трёхмерного объекта по его разноракурсным фотографиям. В случае же двумерных снимков, полученных в результате частичного прохождения сигнала сквозь исследуемый объект (рентгеновское излучение) или же отражения сигнала от поверхности объекта (оптическая когерентная томография), говорят о параллельной проекции.

В частности, для изучения внутренней структуры вещества активно применяется электронная микроскопия: электрон выступает в роли сигнала, проходящего сквозь кристалл. Такой способ позволяет формировать двумерные изображения, являющиеся параллельными проекциями кристаллической решётки с заранее заданной ориентацией наноструктуры в пространстве.

Основной задачей рентген-дифракционного (рент-ген-структурного) анализа вещества является определение параметров модели его кристаллической решётки [5, 6].

С появлением электронной микроскопии стало возможно наблюдать атомарную структуру вещества с высокой степенью точности. В настоящее время линейное разрешение электронного микроскопа достигает порядка 0,1Ǻ [7]. В результате работы электронного микроскопа формируются двумерные изображе- ния, представляющие собой параллельные проекции кристаллической решётки.

Однако из-за того, что двумерное изображение решётки обладает заведомо более низкой информативностью, чем её трёхмерная модель, анализ её параметров по одиночной проекции представляет значительную сложность. Кроме того, в одной из предыдущих работ [8] была разработана модель наблюдаемости кристаллической решётки на двумерной проекции и доказано, что в ряде случаев (нарушение условия наблюдаемости) параметры решётки априори не могут быть оценены верно. Следовательно, разработка метода реконструкции трёхмерной структуры вещества по двумерным проекциям является актуальной задачей, которая позволит значительно повысить точность рентген-структурного анализа.

Модели трёхмерных кристаллических решёток

Элементарная ячейка в кристаллографии является фундаментальным понятием. Она представляет собой особую область кристалла, являющуюся минимальным строительным блоком: всю кристаллическую решётку можно образовать с помощью данной ячейки путём её параллельного переноса (трансляции) по направлениям трёх основных векторов трансляции [9].

Примером элементарной ячейки является ячейка Вигнера–Зейтца [9]. Данная ячейка представляет собой единичную область разбиения диаграммы Вороного, построенной на узлах кристаллической решётки (рис. 1). Так как структура узлов обладает пространственной симметрией, то все области разбиения кон- груэнтны. Однако, несмотря на простоту, универсальность, отражение свойств симметрии кристалла и однозначность построения, трёхмерная ячейка Вигнера–Зейтца является крайне сложным объектом с точки зрения его математического описания. Как следствие, она плохо подходит для оценки индивидуальных параметром кристаллической решётки.

описания: шести параметров (трёх длин трансляционных векторов и трёх углов между векторами) достаточно для задания элементарной ячейки Браве.

Всё множество кристаллических решёток подразделяют на 7 основных кристаллических систем или сингоний (рис. 3). При этом каждая сингония характеризуется не только геометрическими, но и соответствующими физико-химическими свойствами.

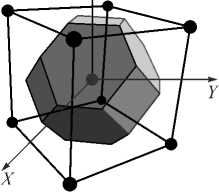
Рис. 1. Элементарная ячейка Вигнера-Зейтца

В связи с возникшими сложностями описания ячейки Вигнера–Зейтца было решено обратиться к другому виду элементарных ячеек – элементарным ячейкам Браве (рис. 2). В отличие от ячейки Вигнера– Зейтца, ячейка Браве является значительно более простым объектом с точки зрения математического

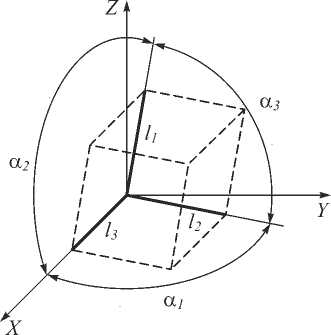
Рис. 2. Элементарная ячейка Браве

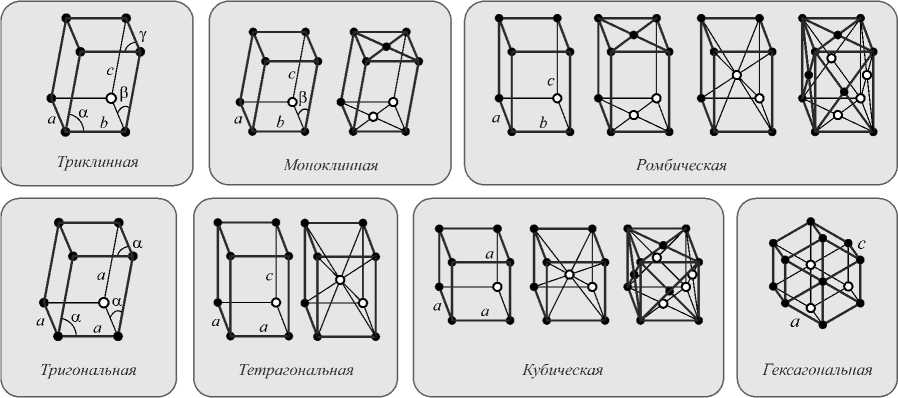
Рис. 3. Элементарные ячейки основных кристаллических систем

Однако элементарная ячейка Браве обладает и существенным недостатком по сравнению с ячейкой Вигнера–Зейтца: возникает проблема неоднозначности выбора элементарной ячейки [9]. Проблема заключается в том, что для одной и той же структуры кристаллической решётки элементарную ячейку можно выбрать множеством различных способов (рис. 4).

Отсюда возникает основная сложность точного определения параметров элементарной ячейки при анализе кристаллической структуры вещества [10–15]. Для повышения точности определения параметров элементарной ячейки требуется, в первую очередь, обеспечить высокую точность восстановления трёхмерной структуры решётки, по которой и будет производиться параметрическая идентификация [16–22].

В связи с этим сложно переоценить важность этапа реконструкции трёхмерной решётки для решения задачи анализа кристаллической структуры вещества.

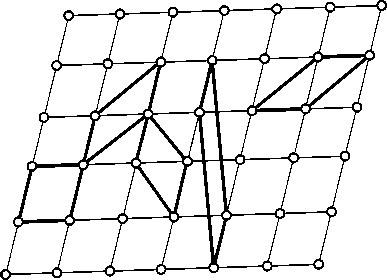
Рис. 4. Варианты выбора элементарной ячейки

Метод трёхмерной реконструкции кристаллической решётки

Кристаллическая решётка задаётся набором узлов в трёхмерном пространстве X = { X : }, l = 1, го . По определению кристаллической решётки данное множество образуется путём параллельных переносов элементарной ячейки и в общем случае является бесконечным:

xl = ia + jla2 + kla3, где a1,a2,a3 – основные трансляционные вектора, il, ji, kl e Z - коэффициенты трансляции.

На практике же, так как известно общее правило формирования решётки, можно ограничиться конечным множеством узлов.

В процессе обработки двумерных снимков электронной микроскопии получаются параллельные проекции решётки, состоящие из набора узлов. Каждая проекция характеризуется положением плоскости в пространстве. Теорема компьютерной томографии о лучевом преобразовании гласит, что любой трёхмерный объект может быть восстановлен по бесконечному количеству лучевых преобразований [23]. Однако кристаллическая решётка формируется по правилу трансляции, поэтому для трёхмерной структуры информативными являются 4 соседних узла, образующие тройку некомпланарных векторов – основных векторов трансляции (все три вектора имеют начало в одном и том же узле). Отсюда следует предположение, что для восстановления трёхмерной структуры кристаллической решётки достаточно использовать три проекции (лучевых преобразования).

В процессе формирования изображения, состоящего из двумерных узлов, возникает погрешность е , которая включает как погрешность самого микроскопа, так и погрешность определения центров узлов.

Введём обозначение: P = ({ z l } L =1 , Ф ) - проекция, содержащая L двумерных точек и заданная в пространстве матрицей Ф. Для удобства будем считать, что проекция, лежащая в плоскости XOY, имеет матрицу Ф = E . Проекция представляет собой плоскость в пространстве, проходящую через нулевой вектор линейного пространства и задаваемую вектором-нормалью. Тогда нормаль плоскости для заданной проекции будет определяться следующим выражением:

п = Ф ( 0 0 1 ) T . (1)

Если матрица Ф задаёт ориентацию плоскости проекции в трёхмерном пространстве, то обратная матрица Ф–1 будет переводить из двумерного пространства плоскости проекции в стандартное трёхмерное пространство, то есть двумерные узлы переводятся в трёхмерное пространство с использованием выражения:

у = Ф^{- 1} ( z , z 2 0 ) T . (2)

Рассмотрим две проекции P ₁ и P ₂. Пусть n ₁ и n ₂ – нормали соответствующих плоскостей.

Выберем точку y ₁ на проекции P 1 . Проведём прямую с направляющим вектором n ₁ через точку y 1 . Уравнение прямой будет задаваться следующим выражением:

x = n 1 t + У 1 . (3)

Выберем точку y 2 на проекции P 2 . Спроецируем прямую на плоскость другой проекции и рассмотрим 3 ключевых расстояния (рис. 5): расстояние d от спроецированной прямой до точки у ₂, расстояние D _Y от точки y 2 до прямой (3), расстояние D от прямой (3) до спроецированной прямой. Заметим, что расстояние от прямой (3) до спроецированной прямой есть расстояние от прямой (3) до плоскости проекции P 2 .

По представленной схеме можно вывести расстояние d ², которое будет зависеть от свободной переменной t . Переменная t определяет точку на прямой (3). Интерес вызывает только такая точка, которая обеспечивает минимум d ². Если точка y 2 окажется достаточно близкой до прямой (3), то есть d <  е , то соответствующую точку на прямой (3) будем считать кандидатом на восстанавливаемый узел решётки.

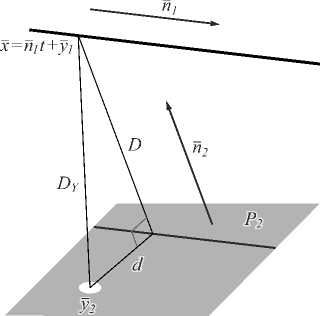
Рис. 5. Проецирование прямой на плоскость проекции и иллюстрация ключевых расстояний

После вычисления всех кандидатов на восстанавливаемые узлы решётки необходимо исключить дублирующие узлы, которые образовались при восстановлении с разных пар проекций, но при этом представляют один и тот же узел в пространстве с учётом заданной погрешности е .

Таким образом, метод реконструкции на основе минимизации расстояния до узла на проекции заключается в выполнении следующих этапов:

• •    выбор опорной проекции P_k ;

• •    для каждой пары проекций ( P 1 , P ₂):

o вычислить векторы нормалей к плоскостям проекций n 1 и n 2 ;

o выбрать узел z 1 на проекции P 1 и узел z 2 на проекции P ₂, вычислить векторы y ₁ и y ₂ с помощью обратной матрицы Ф^–1;

o сформировать множество узлов в трёхмерном пространстве X ^ˆ , соответствующее трёхмерной структуре кристаллической решётки:

• ■      5 1 = пТ n ₂;

• ■     t i = ( 5 1 П Т У 1 - П Т ( У 1 - У 1 ))/ ( ! - 5 2 ) ;

• ■    X = п t + У;

• ■    D = п Т X 1 ;

• ■     d ² =|| x _t - y ||² - D ² ;

• ■    если d ² <5 d ², то X = X u { X 1 } ;

• •    объединить все узлы из множества X, для которых верно d ( X , x, ) <5 d , в кластеры D q : q = 1, Q , где Q - количество найденных кластеров;

• •    для каждого множества D_q произвести усреднение:

^Xq = I S ^{x .}

| Dq| X е D q

Таким образом, формируем множество

X = { X „| -.

I qX =1, Q

Множество X ^ˆ будет содержать восстановленные узлы с учётом заданной допустимой ошибки s . Полученное множество может использоваться в дальнейшем для проведения параметрической и структурной идентификации кристаллических решёток в трёхмерном пространстве [18–22].

Оценка погрешности реконструкции

Для узла y , переведённого из двумерной плоскости в пространство действием матрицы Ф^–1 на соответствующий двумерный узел проекции, искажение представляет собой выражение:

у = у + 5 , где ||5||<5 .

Введём обозначение:

c =

II+ 2 - п Т П1

Подставляя искажённый узел в формулу для t , получаем следующее выражение:

t 1 = t 1 + с ( nT [ п 2 ( п Т 5 ) -5 +5 2 ] ) ,                (5)

где 5 k - погрешность определения узла у 1 ; 5 l - погрешность определения узла y ₂ ; t k – точное значение параметра t .

Искажённый восстанавливаемый узел представляет собой выражение:

—   — 7 . —

X 1 = П 1 1 1 + у 1 .

Подставляя (4) и (5) в (6), получаем:

X 1 = П 1

' 1 ^{+ 5} 2 ] ) ) + У 1 ^{+ 5} 1 . ⁽⁷⁾

Отбрасывая точное значение в (7), получаем формулу вектора ошибки (8).

5 d = СП 1 ( П 1^Т [ п 2 ( п 2 ^Т 5 2 ) - 5 1 +5 2 ] ) + 5 1 .              (8)

Оценивая норму вектора (8), получаем следующую общую оценку для погрешности:

II⁵ d l <⁵+

|||Й 11|2 - пTU 1 1

Для ортогональных проекций норма (9) ограничивается значением 4 5 . Допустимое расстояние между точкой на проекции и спроецированной прямой ограничивается таким же значением, поскольку максимальное отклонение восстанавливаемого узла x ₁ совпадает с максимальным отклонением соответствующего узла на проекции. Таким образом, для ортогональных проекций s = 4 5 d .

Исследование точности трёхмерной реконструкции кристаллических решёток

Для проведения экспериментов были сгенерированы 7000 решёток – по 1 000 решёток каждой кристаллической системы: триклинной – aP , моноклинной – mP , ромбической – oP , тригональной – hR , тетрагональной – tP , гексагональной – hP , кубической – cP . При моделировании длины сторон элементарных ячеек варьировались от 1 Å до 10Å, величины углов – от 5° до 175°. Каждая смоделированная решётка проецировалась на 3 ортогональные проекции, узлы которой искажались на значение 5 d =0,1. К сформированным проекциям применялся описанный выше алгоритм реконструкции кристаллической структуры.

Для анализа точности реконструкции кристаллических решёток необходимо сравнить полученную трёхмерную структуру с исходной смоделированной структурой [16, 17, 24]. Будем использовать метрику Хаусдорфа для сравнения множеств узлов.

Кристаллические решётки подразделяются на семь основных кристаллических систем. Проведём анализ разделимости типов кристаллических систем. Для каждой восстановленной решётки и всеми исходными решётками вычислим расстояние Хаусдорфа. Будем относить восстановленную решётку к тому типу, расстояние до которой оказалось минимальным. Такой анализ относится к задачам структурной идентификации [16, 18, 19].

Схему предлагаемого вычислительного эксперимента можно разделить на 4 этапа (рис. 6):

• 1.    Моделирование двумерных проекций.

• 2.    Восстановление трёхмерной структуры решёток.

• 3.    Идентификация параметров элементарных ячеек.

• 4.    Проведение структурной идентификации путём сравнения с базой эталонных параметров.

Результаты проведения экспериментов представлены в табл. 1.

Полученные результаты показали, что в 6 случаях из 7 тип реконструированной решётки определяется верно, а, следовательно, сам процесс реконструкции прошёл с достаточной точностью. В случае моноклинных решёток произошло критическое падение точности идентификации до 34%. Однако если посмотреть на рис. 1, то можно увидеть, что ромбиче- ские решётки являются вырожденным типом моноклинных – данный факт и был подтверждён в ходе исследований, так как система в 53% случаев определила восстановленную моноклинную решётку как ромбическую.

Кроме того, особое внимание привлекает факт несимметричности таблицы результатов. Наиболее ярко данное свойство прослеживается для моноклинных и гексагональных решёток. Казалось бы, во всех экспериментах используется один и тот же набор решёток, однако причина подобной несимметричности кроется в геометрических особенностях разделения решёток на классы. Например, ромбическая решётка при искажении может «потерять» свою главную отличительную особенность, – прямой угол, – и стать моноклинной. В обратную сторону такое событие почти невозможно, так как вероятность того, что при случайном искажении непрямой угол ячейки станет прямым, чрезвычайно мала. Следовательно, выявленная особенность лишь подтверждает корректность постановки эксперимента.

I этап

Моделирование двумерных проекции

II этап

Восстановление трёхмерной структуры

III этап

Идентификация параметров

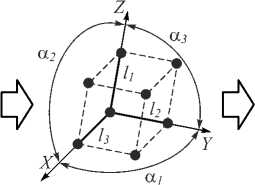
IV этап

Поиск схожей решётки -структурная идентификация

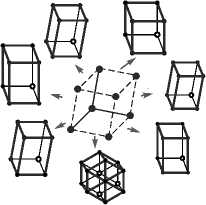
Рис. 6. Схема проведения эксперимента

Табл. 1. Результаты структурной идентификации реконструированных кристаллических решёток

Реконструированная решётка	Смоделированная решётка
	cP	hP	mP	oP	tP	aP	hR
cP	99,9	0	0	0	0	0	0,1
hP	0	100	0	0	0	0	0,0
mP	0,2	0	34,1	53,1	10,3	2,1	0,2
oP	0	0	0	100	0	0	0
tP	0	0	0	0	100	0	0
aP	0	0,2	0,8	0,2	0	98	0,8
hR	3,7	0	0	0,1	0	1,5	94,7

Следует отметить, что указанную несимметричность таблицы можно устранить только одним путём – моделированием такого количества решёток, которое бы равномерно заполнило всё пространство параметров элементарных ячеек с шагом, меньшим, чем допустимая величина ошибки идентификации. Однако данный подход, с одной стороны, привёл бы к непомерному росту вычислительной сложности (увеличение выборки на несколько порядков), а с другой стороны, внёс лишний «шум» в виде огромного количества триклинных решёток (на которые, в общем случае, похожи решётки всех остальных типов).

Таким образом, в ходе эксперимента было получено два важных результата: во-первых, доказано высокое качество восстановления трёхмерной структуры решётки с помощью разработанного алгоритма. А во-вторых, показана проблема разделимости моноклинных и ромбических решёток, где единственное отличие первых – это наличие угла «не равного 90°».

С другой стороны, следует также отметить, что сама метрика Хаусдорфа не учитывает проблемы плохой разделимости кристаллических систем, что является следствием проблемы неоднозначности выбора элементарной ячейки Браве. В связи с этим для проведения исследований разделимости кристаллических систем рекомендуется либо исключать из общей выборки «похожие» решётки (что является, вообще говоря, нетривиальной задачей), либо использовать метрику схожести, способную учитывать описанную особенность кристаллических решёток. Именно на втором подходе и планируется сконцентрировать внимание в дальнейшем.

Заключение

Рассмотренный алгоритм реконструкции кристаллических решёток по двумерным проекциям позволяет восстановить трёхмерную структуру решётки на основе трёх проекций. Для сравнения, стандартные методы компьютерной томографии вынуждают использовать более сотни проекций, однако такой подход избыточен в случае кристаллов с периодической структурой. Кроме того, он требует существенно больших объёмов вычислений, не предоставляя большей точности восстановления, так как не учитывает периодический характер кристаллической решётки.

Проведённое исследование показало высокое качество восстановления трёхмерной структуры: для 6 из 7 кристаллических систем восстановленные решётки совпали с исходными. Побочным результатом исследований стало обнаружение факта плохой разделимости моноклинных, ромбических и тетрагональных решёток, вызванного недостатками используемой метрики Хаусдорфа, которая не может бороться с проблемой неоднозначности выбора элементарных ячеек.

Работа выполнена при частичной поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности Самарского университета среди ведущих мировых научно-образовательных центров на 2013–2020 годы; грантов РФФИ № 16-41-630761, № 17-01-00972, № 18-37-00418, в рамках госзадания по теме № 00262018-0102 «Оптоинформационные технологии получения и обработки гиперспектральных данных».