Алгоритм решения многокритериальной задачи о назначениях на сетях

Практика проектного менеджмента показала, что весьма часто реализуемые проекты не оканчиваются успешно из-за превышения ограничений по времени и/или стоимости [1]. Такая ситуация характерна и для России. Одной из главных причин является, по нашему мнению, принятие недостаточно обоснованных управленческих решений относительно назначения исполнителей на выполнение отдельных работ по проекту.

Реализация сложных проектов требует выполнения совокупности взаимозависимых работ, связи между которыми хорошо описываются с помощью сетевых графиков – ориентированных взвешенных графов без петель и контуров, элементам которых поставлены в соответствие некоторые характеристики. При этом события (факт окончания или начала выполнения работ) соответствуют вершинам графа, а работы – дугам, ориентация которых соответствует технологии этого процесса.

Методы сетевого планирования основаны на идее оптимизации критического пути и являются эффективным средством составления проектов и наблюдения за их выполнением [2].

В настоящее время существует несколько вариантов сетевой модели управления проектами, например, [3–5], центральным моментом которых является оптимальное назначение исполнителей на заданный перечень работ.

В качестве критерия используется суммарное время реализации проекта, либо длина критического пути на графе. Как вариант, на длину критического пути может накладываться ограничение по директивным срокам.

Таким образом, суммарное время, затраченное на реализацию проекта, и длина критического пути представляются одинаково важными характеристиками реализации проекта, и их следует рассматривать как два равноценных критерия многокритериальной задачи управления проектом. Нами предложен алгоритм, вообще говоря, приближённого нахождения множества Парето-оптимальных решений данной задачи.

Исходные параметры математической модели

Пусть I = {1..., n } - множество всех работ (операций); J = {1, 2..., n } - множество исполнителей; без ограничения общности можно считать, что число работ и исполнителей совпадает, в противном случае несложно провести дробление работ на более мелкие или ввести фиктивных исполнителей.

V ij - время, которое требуется j -му исполнителю для выполнения i -й работы; при фиксированном назначении V ij можно интерпретировать как вес (длину) i -й дуги графа.

Варьируемые параметры математической модели

Z ij е {0; 1} - распределение операций по исполнителям: Z y = 1, если i -я операция поручена j -му исполнителю, Z ij = 0 в противном случае.

y i - фактический срок окончания i -й операции; он вычисляется после назначения исполнителей на работы как суммарная длина дуг критического пути P ( i ), ведущего от начальной вершины 1-й по сроку операции к конечной вершине i -й операции:

• У. = Е Е VZ v е I^d .

k ∈ P ( i ) j ∈ J

Для поиска критического пути существует несколько алгоритмов, например, описанный в источнике [6].

Ограничения математической модели

Каждая i -я работа может начать выполняться только после выполнения всех работ, предшествующих ей.

Каждая работа выполняется лишь одним исполнителем:

Е Z j = 1 ^{V i} е I           (1)

j ∈ J

Каждому исполнителю поручается лишь одна работа:

Е Z_ti = 1 V j е J          (2)

∈ I

Целевые функции.

Минимизировать суммарное время выполнения проекта

ЕЕ V j Z j ^ min       (3)

∈ I j ∈ J

Минимизировать протяжённость критического пути в графе max y ^ min           (4)

∈ I

Алгоритм решения

Хотя к настоящему времени предложено несколько методов решения таких моделей, основанных на целочисленном и булевском программировании (например, в [7, 8]), высокая размерность задач препятствует их успешному применению. Поэтому авторы предлагают новый комбинированный алгоритм.

При использовании частного критерия (3) мы имеем обычную задачу о назначениях. Известно несколько методов решения этой задачи, наиболее простой - метод Мака [9]. Для приближённого решения многокритериальной задачи предлагается алгоритм линейной свёртки критериев (АЛСК). Как известно [10], в общем случае использование линейной свёртки не гарантирует нахождение всех эффективных решений дискретной многокритериальной задачи. Вопрос же о полной разрешимости сетевой многокритериальной задачи о назначениях посредством АЛСК в настоящее время не исследован, поэтому предлагаемый нами метод следует трактовать как приближённый.

Описание алгоритма

• 1.    Решаем классическую задачу о назначениях. Очевидно, что найденное решение доставляет минимум критерию суммарного времени и максимум на множестве Парето критерию протяжённости критического пути.

• 2.    Далее за счёт перераспределения работ стремимся улучшить значение критерия (4). Для этого умножим возможные веса V ij всех дуг, участвующих в критическом пути на некоторый коэффициент а > 1. Тем самым увеличим значимость этих работ. Далее решаем новую задачу о назначениях.

• 3.    Посредством увеличения значения а получаем новые Парето-оптимальные решения.

Пример. Имеем модель процесса реализации проекта в виде графа, представленного на рисунке 1.

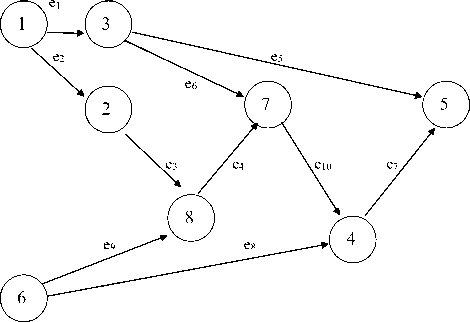
Рисунок 1. Граф процесса реализации проекта

Figure 1. The graph of the project implementation process

Номера дуг указывают номера работ. Матрица длительностей выполнения работ в количествах условных временных единиц имеет вид:

1	2	3	4	5	6	7	8	9	10
29	16	19	28	13	39	11	13	11	15	| 1
21	19	38	18	18	26	37	30	32	17	| 2
34	24	23	28	34	26	37	25	25	37	| 3
26	17	16	31	11	17	34	33	24	11	| 4
21	35	37	17	38	25	13	31	37	25	| 5
38	16	39	14	32	29	18	37	28	15	| 6
36	17	23	19	25	30	20	37	29	39	| 7
27	15	13	20	27	22	30	20	36	31	| 8
29	17	18	23	17	21	14	31	34	25	| 9
28	23	22	25	24	40	32	16	27	24	| 10

Решаем задачу о назначениях с данной матрицей. Получаем следующее распределение операций по исполнителям (первая эффективная точка).