Алгоритм решения многокритериальных задач управления

• ¹    Самарский научный центр РАН

• ²    Самарский государственный аэрокосмический университет

Рассматривается задача формирования управления сложной системой, исходя из минимизации векторного критерия качества, при наличии ограничений на параметры состояния и вектор управления. Предложен подход к решению задачи с использованием аппроксимации множества Парето, на основе которого разработан алгоритм формирования управления. Обоснованы условия сходимости алгоритма.

Формулировка задачи

Рассматривается процесс функционирования управляемой системы при наличии ограничений на параметры состояния и вектор управления. Состояние системы в каждый момент времени определяется вектором управления и , принадлежащим допустимой области U :

и е U .

На параметры состояния управляемой системы наложены ограничения

Gj[u] < 0,j = 1,...,J.(2)

Целью функционирования системы является минимизация векторного критерия качества

Rk[u],k = 1,...,K.(3)

Таким образом, для управляемой системы требуется определить вектор управления в соответствии с ограничениями (1) и (2)

и eU = { u eU, G j [u] <  0,j = 1,...,J } , (4) минимизирующий векторный критерий (3).

Парето-оптимальные и минимаксно-оптимальные решения

В сформулированной задаче соотношения (2) и (3) задают отображение ^:U ^ Ф , где Ф - область допустимых значений критериев, образуемая допустимыми значениями векторов R_k[u](k = 1,...,K) при управлениях, удовлетворяющих условиям (4). В дальнейшем используется множество индексов K = { k = 1,2,...,K } .

Решение многокритериальной задачи приводит к формированию множества не-улучшаемых по Парето ( П -оптимальных) управлений u* [1], принадлежащих множеству U . Множество Парето представляет собой совокупность управлений, определяемых из условия

u * е U| 3u е U: R_k [u] <  R_k [u * ], [k е K , u , u *

Управления, входящие в множество Парето, являются несравнимыми по векторному критерию, вследствие чего возникает проблема выбора единственного управления из множества Парето. Единственность решения задачи (1)-(4) может быть обеспечена с помощью принципа гарантированного результата (минимакса) [2], согласно которому оптимальным считается управление u ^о из множества U , которое доставляет наилучшее значение наихудшему критерию качества:

u^o = arg min max R_k[u] .     (6)

ueU keK          "

Важным свойством управления, сфор мированного в соответствии с принципом минимакса, является наличие наибольшей окрестности, внутри которой управление может варьироваться при необходимости парирования априорно неопределенных факторов.

Нормализация критериев

Критерии Rk,k е K имеют разный смысл и разные диапазоны изменения. Нор- мализация критериев при управлении и выполняется по формуле:

⁵ k ^[u] =

R k [u] - R kmin

5 2 = a ( 5 . )^- b           (10)

с коэффициентами

max

^R k

n min

^R k

,k е K ,    (8)

b = In 5"2 - ln 5 2

in 5 1 - in 5 1

^a = ⁵ 2 ( ⁵ 1 ) ^b .

где 5 k [u] - нормализованное значение k-го критерия; Rm” - минимальное значение k-го критерия, полученное в результате решения однокритериальной задачи оптимизации без учета остальных критериев, достигаемое при управлении um^m ; R ^max - максимальное значение k-го критерия, определяемое как наибольшее среди значений, соответствующих управлениям, при которых остальные (K-1) критериев при тех же условиях достигают минимумов.

Для нормализованных критериев принцип минимакса определяется следующим образом [3]: задача (1)-(4) при равнозначных критериях решена, если найдено управление u⁰ eU , для которого

5 0 [u ⁰ ] = mi n max 5 _k[u ] ueU keK         '

Аппроксимация множества Парето

Приближенно управление, оптимальное по критерию (9), может быть получено с использованием аппроксимации поверхности ^(П), образованной сочетаниями критериев при п -оптимальных управлениях в K-мерном пространстве критериев. В соответствии со свойствами множества Парето [3] поверхность ^(П) строго монотонна и представляет собой левую нижнюю границу множества Ф. Поверхность ^(П) является выпуклой, если множество Ф выпукло. В этом случае поверхность ^(П ) может быть аппроксимирована гиперповерхностью.

В двухкритериальной задаче гиперболическая кривая (рис.), проходящая через точки аппроксимации

А' ( ^ 1 >^ 2 ) ^и А" ( ^ 1 ,^ 2 )

с

центром в начале координат и асимптотами - координатными осями (в результате нормализации критериев) определяется уравнением

В задаче с тремя критериями качества уравнение аппроксимирующей поверхности имеет вид

5 3 = a(5, У" (52 У ■ и коэффициенты a,b,,b2 вычисляются по формулам

• b, = A^ / A, b, = Ab2 / A, a = 53 (5,)‘‘ (52)b2,

где

A = ( in 5 1 - in 5 2 )( in 5 2 - in 5 ³ ₂ ) - | - ( in 5 1 - in 5 1 )( in 5 3 - in 5 2 ) , a _b1 = ( in 5 2 - in 5 3 )(in 5 2 - in 5 2 ) - - ( in 5 3 - in 5 3 )( in 5 2 - bl 5 2 ) , a . = ( in 5 1 - in 5 2 )( in 5 3 - in 5 3 ) - - ( in5 1 - in5 3 )( in5 3 - in5 3 ) .

В общем случае К критериев уравнение аппроксимирующей гиперповерхности, проходящей через К точек аппроксимации A^k ( 5 k ,5 2 '---,5 K ) ,k е K , имеет вид

5 К = a ( 5 1 )^{- b1} ( 5 2 )^{- b2} ... ( 5 К - 1 )^{- bK - 1} (¹²) с коэффициентами a,b 1 ,b 2 ,...,b K _- 1 , получае-

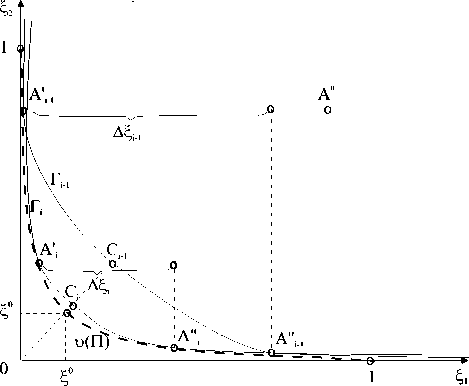
Рис. Формирование аппроксимирующих гипербол

мыми в результате решения системы уравнений

^ K = a$ f¹ (^" b ... ( ^ K - 1 y^{b K - 1} ,k = 1,2,...,K .(13)

Методика использования аппроксимирующих гиперповерхностей

С учетом свойства, сформулированного в [4], нормализованные критерии при минимаксно-оптимальном управлении равны между собой. В двумерном случае точка, образованная сочетанием критериев при этом управлении, принадлежит биссектрисе первого квадранта. Вследствие этого координаты вершин аппроксимирующих гипербол (точки C_t, C i _- 1 на рис.) соответствуют приближенным решениям двухкритериальной задачи.

Для формирования управления, являющегося приближенным решением многокритериальной задачи, необходимо

• •    определить K векторов управления, обеспечивающих сочетания критериев, при которых значения (K-1) критериев фиксированы, а один критерий достигает минимума, • определить коэффициенты аппроксимирующей поверхности путем решения системы (13),

• •    вычислить координаты вершины аппроксимирующей поверхности по формуле

  У =S C

  
  

  к г = ( a )

  
  

  ^b 1 ^{+ b} 2 + ... + ^b K - 1 ^{+ 1} .

  
  

Сочетание критериев в вершине аппроксимирующей поверхности и соответствующий вектор управления представляют собой приближенное решение многокритериальной задачи.

Уточнение приближенного решения может быть выполнено с помощью итерационной процедуры минимизации максимального для данного приближения критерия при фиксированных значениях других критериев. Управление, полученное в результате скалярной минимизации, позволяет сформировать соответствующую аппроксимирующую гиперповерхность, координаты вершины которой являются опорным управлением на следующей итерации.

Сходимость итерационной процедуры обеспечивается за счет выбора шага i-й ите рации A^i- (рис.) таким образом, чтобы выполнялось условие

А

■ Р A"

- min с,¹ k e K

<^A5 i <^A5 i - 1 ,

за счет чего вершина аппроксимирующей гиперповерхности на каждой итерации оказывается между точками аппроксимации A " и Л " .

Шаг на i-й итерации предлагается вычислять по формуле

A^ i =

^A ^ i- 1 ^{+ 5} C 1 ^- min ^ A¹ keK

Алгоритм решения двухкритериальной задачи

В случае K=2 аппроксимирующая кривая является гиперболой. С учетом нормализации (8) центр гиперболы принадлежит началу координат, так как асимптотами являются координатные оси. Линия ^ (П) п-опти-мальных сочетаний критериев имеет вид, показанный на рис.

Предлагается следующий алгоритм формирования минимаксно-оптимального управления:

• 1)    Решаются задачи скалярной минимизации критериев R k [ u ], k e K . Определяются управления u min и соответствующие им минимальные значения каждого критерия R min , k e к без учета остальных критериев.

• 2)    Определяются максимальные значения каждого критерия

maxmin

Rk = max Rkun J,ke K -neK ,n^k*

• 3)    Выбирается начальный закон управле-~

ния u e U среди u_k ,k e K .

• 4)    Задается начальное значение шага

A А <  1 .

• 5)    Определяется опорное управление, тождественное начальному и = u^H при i = 0 (i - номер итерации), или полученному на предыдущей итерации и = u iE; при i >  0 ;

• 6)    Определяется критерий с наибольшим нормализованным значением

^к' = max %к[щ] кеК и фиксируется значение другого критерия R k = Rk [ui], к * к'; область U дополняется ограничением

U' = { и eU,R^k [и] = R^k ,к * к' } ;

• 7)    Формируется управление и^к , удовлетворяющее условию минимальности

^ к' ^[и^г к‘ ] = min ^ к'^[ и]^к' е К, и eU'

и вычисляются координаты точки А( ^ 1гЛ 2г) , принадлежащей множеству J (П) ;

• 8)    Определяется значение шага итерации A ^ i = A K ^{^} при i = 0 или

• A^i-1 + К Ci-1 - min^Ai

Ac =---------1---------'----- при i > 0. Вычисляется значение критерия с номером к', соответствующее этому приращению (8):

R k = ( K k U k - ] +A ? i )( R k- - R” n ) + R“ .

-^~

Область U дополняется ограничением;

U~' = {i e U~,R k [ u ] = R k } .

• 9)    Формируется управление и ^к , удовлетворяющее условию минимальности

^к"[игк"] = min ^г1'"[и],к;''е К, и eU''

и вычисляются координаты точки 4(Kn^i) ;

• 10)    Вычисляются координаты вершины гиперболы

^ 1 = ^ 2 = ^{( a ) b} + ¹,

• 11)    Формируется управление u c , соответствующее точке C ( ^ C , ^ C ) или ближайшей к ней точке, если C i й Ф ; для этого по координатам точки Ci определяются значения исходных критериев

CC max min min

Rk =Ski(Rk - Rk ) + Rk ,к е K и находится управление и из условия принадлежности области

U C = { и eU, R^k [и] = R_k ^C ,k е к } , если C i еФ , или, если C i йФ , из условия min _~ max R^k [и] - R C ■ иeU к еК               । ’

• 12)    Проверяется условие окончания итераций |^ C - 1 - ^ C А £ . Если оно выполнено, то точка C i считается приближенным минимаксно-оптимальным сочетанием критериев, а ее прообраз ui ^C - минимаксно-оптимальным управлением и⁰ ; в противном случае вычисления повторяются, начиная с шага 5.

Алгоритм решения многокритериальной задачи в общем случае

В общем случае К критериев алгоритм имеет вид:

• 1)    выбирается начальный закон управления u^{^} е U ; задается начальное значение

шага АК ^{^} <  1 ;

• 2)    определяется опорное управление по правилу

{ и_н при i = 0, _C и_{{ -} 1 при i > 0;

• 3)    формируется К управляющих зависимостей и к ,к е К путем последовательного решения К задач минимизации

^к[игк] = min max^к[и],к = 1,...К, и£Uki кеК

Uh= [и eU,Rk [и] = Rg , к * argmax ^к[и'к_1],к е к! I                                   к еК                    J в каждой из которых

Rk = ^k(Rmax -Rmin; + RminЛк = ^k-1 + A^i, где ^ к-1 - значение к-го критерия, полученное в результате предыдущей задачи. В каждой из К задач начальным приближением служит управление Ui при к=1, ик-1 при к=2,3,...,К; при этом шаг итерации равен

A K i =

A K i - i + K ^Ci^-1 - min K A i к е к

• 4)    вычисляются координаты точек A ^k (5^,5 21 ,-,5 ^k _Ki),k g K, принадлежащих множеству ^(П) ;

• 5)    вычисляются координаты вершины гиперповерхности C i = (5 % ,%^... ^кб )

^) И = ⁵ 2i =---=⁵ Ki = ^ i = ( a ^{) b} 1 ^{+ b}2 +-+b_K - 1 ^{+ 1} , где коэффициенты b 1 ,b₂,...,b_K _ 1 определяются из решения системы

5K = a'^ )"b' (5 I •••(?K-1) '" ,k = 1,2 K

• 6)    формируется управление u ^C , соответствующее точке C i или ближайшей к ней точке, если C i ^ Ф ; для этого по координатам точки C i определяются значения исходных критериев

C cC _/Dmax _Dmin    _nmin

^Rk = ⁵ ki^(Rk ^{- R}k ) ^{+ R}k ^{,k G K} и находится управление u из условия принадлежности области

Uc = {u g U, Rk[u] = Rk ,k g k}, если Ci GФ, или, если Ci ^Ф, из условия ющие смежным итерациям, определяются уравнениями (рис.)

Г - 1 : 5 2 = f -1 ( 5 1 ) , Г : 5 2 = ft ( 5 1 ) .

Пусть приращение A5 i подбирается таким образом, что на каждой итерации точки A i и A i лежат на гиперболе по разные стороны от точки C i . В этом случае можно подобрать такое 5 g [ 0,1 ] , что

5 С =55 * + ( 1 -8 ) 5 k , 0 <5< 1, k = 1,2 .

Поскольку гипербола является выпуклой кривой, то из условия выпуклости

.f ( §5 k + ( 1 - 5 ) 5 k ) <  5f ( 5 k ) + ( 1 - 5 ). f ( 5 k ) - для любого 5 g [ 0,1 ]

вытекает, что

5 C = f ( 5 C ) = f ( 55 1 + ( 1 - 5 ) 5 1 ) < 5 f ( 5 1 ) + ( 1 - 5 ) f ( 5 1 ) =

= 55 2C - 1 + ( 1 -5 ) f {5 1’ )             (15)

’ ’

Так как по построению точки Ai верно неравенство f (51 ) = fi (5 C-1 )<5 C'-1 ,      (16)

min max R^k [u] - rC\ ■

'

u g U k g K

;

то при подстановке 5 ^C _{- 1} вместо f ( 5 i ) не

• 7)    проверяется условие окончания ите-

• равенство (15) не изменит знака

р^ац^{ий 5 C}_₁ ^-5 ^C

< £ . Если оно выполнено,

то точка C i считается приближенным минимаксно-оптимальным сочетанием критериев, а ее прообраз u^C - минимаксно-оптимальным управлением u ⁰ ; в противном случае вычисления повторяются, начиная с шага 2.

Условия сходимости алгоритма

Алгоритм позволяет определить минимаксно-оптимальное сочетание критериев 5 за конечное число итераций, то есть для заданной точности £ >  0 найдется такой номер i, что

|50 -5C\<£•(14)

5 C- = 5% Ci - 1 + ( 1 -5 ) 5 C - 1 5 C - 1 • (17)

С учетом того, что по свойству симметричности [5]

51C = 5 C = 5 C,(18)

из (17) следует невозрастание последовательности точек { 5 ^C }

5 C <5 C-1 •(

С другой стороны, по свойству симметричности (18) и свойству минимальности

5\[uk] = min 5\[u].k g k ugU сочетание критериев 5 ° при минимаксно оптимальном управлении u° ограничивает

Для случая К=2 гиперболы, соответству

последовательность точек

{5 C}

снизу:

• £ ° = min ^ _k, k = argmax ^ _k .

u e U            k e K

Таким образом, существует предел lim ^C = ^°, i ^~ а это означает, что начиная с некоторого номера i выполнится условие (14).

Заключение

Решение многокритериальной задачи на основе предложенного алгоритма сводится к последовательности скалярных оптимизационных задач и предусматривает:

• а)    формирование К Парето-оптималь-ных управлений;

• б)    построение в соответствии со значениями критериев при этих управлениях гиперболических поверхностей (кривые r i ,r i1 на рис.), аппроксимирующих поверхность Парето в пределах малой окрестности опорного управления;

• в)    нахождение точки сочетания критериев, принадлежащей аппроксимирующей поверхности и имеющей равные нормализованные значения критериев, и формирование соответствующего управления.

Предложенный алгоритм позволяет определять минимаксно-оптимальное сочетание критериев ^ 0 как в случае выпуклого к началу координат множества ^(П), так и в невыпуклом случае, поскольку на предпоследнем шаге в невыпуклом случае ищется точка, ближайшая к C в смысле u = argminmaxti[u] — £C .

u e U k eK              ' '

Алгоритм, кроме того, позволяет учесть приоритеты критериев, задаваемые коэффициентами важности вk:

к

^вk = 1, вk > 0, k e К.

k = 1

В этом случае алгоритм применяется в неизменном виде, но нормализованные критерии подвергаются преобразованию:

5 ^k =в ^k £ ^k, k e К .

Таким образом, предложенный алгоритм, формируя минимизирующую последовательность управлений, сводит решение многокритериальной задачи управления к последовательности решения скалярных задач оптимизации, для которых разработаны надежные численные методы решения, в частности, [5].