Алгоритм решения разреженной системы линейных алгебраических уравнений большой размерности с использованием метода сопряжённых градиентов

При решении задач идентификации параметров динамических систем по экспериментальным данным [1–3] возникает необходимость решения разреженных систем линейных алгебраических уравнений большой размерности специального вида.

Рассмотрим систему линейных алгебраических уравнений следующего вида:

My = d,

где

M = (

H	T T	A T
T	0	0
■ A	0	0

) -0 -® s, d e R2N+4, ^, d2 e R2, A, d, e R2(N-1),

O – нулевые матрицы соответствующих размеров,

H =

< B O1

B O,2

—I

N 2 N

B O

B O, N -1    B O, N

B 2, O	B o,i = B Ti’O ’ B i ’ O = O 2 x 4 ’
в	,       i = V N ,
N -1, O
B N ’O	boo = O 4 .
B OO >

Iin — единичная ( 2 N x 2 N ) -матрица, O₄ — нулевая ( 4 x 4 ) -матрица, O_2Nx4 — нулевая ( 2 N x (2 N + 4) ) -матрица,

T - единичная ( 2 x 2 ) -матрица, T i ( 2 x 4 ) -матрица,

T = [ T 1 , T 2 ,..., T N , T o ] ,

( i = 2, N ) - нулевые ( 2 x 2 ) -матрицы, T _O — нулевая

A =

( D

D 2

K 2

E 1

E 2

,

^DN - 1

E

Di =

1+to

2  1

^TO 2  ³

^TO 2  ²

1 + TO 4

,

K =

-11 - TO

I 2  1

TO 2  3

2 ^O 2

4 - 2 ^O 4

,   O k g R, k = 1,4,

E =

2^{( x}i ,1 ^{+ x}i + 1,1 )

2 ⁽ x i ,2 ⁺ x i + 1,2 )

2 (xi,1 + xi+1,1)   2 ( xi,2 + xi+1,2 )

,

i = 1, N -1.

Компоненты вектора d вычисляются по формулам d =-H(z-z), d = h-Tz, d =-g(z), g (z) = column (g (z) ,..., gN-1 (z)) , gi (z) = Column (gi,1 (z) , gi,2 (z)) ,   i = 1 N -1 .

z = column ( xN, O) g R2 N+4, z = column ( xN, O4 ) g R2 N+4,  H2 = -^ HT H 1, xN = column (x,...,xN)gR2N, x = column (xpx2)gR2,    i = 1,N,

( T i gi,1 ( z ) = gi,1 ( XN ’ O) = I 1 + — O1 I xi,1

+ jO ₂ x 2

-(i-Lg L + Lg x

I 2 ^1 I x i + 1,1 ⁺ 2 ^U2 x i + 1,2 ,

i = 1, N - 1,

T g i ,2 ( z> g i ,1 ( ^X N ^{, O} ) = — ^O 3 x i ,1

⁺ ( ^{1 +} T^O 4 J x i’²

+ ^0.x^ -I 1 - TO4 I xi+1,2,

i = 1, N - 1,

Для приближенного нахождения решения системы (1) использовался метод сопряженных градиентов. Приведем алгоритм метода сопряженных градиентов [4] для системы (1):

1.    Выберем начальное приближение у(0). 2.    г(0) := d — Му^0^, р(0) := г(0), j := 1. 3.    Вычислим коэффициент aj := (г(\г(>))/(Мр(\р(>)). 4.    Найдем следующее приближение у^1 := у(^ + ajp(j). 5.    Вычислим поправку к решению г(j+1^ := г(j) — ajMp(j). 6.    Найдем коэффициент Pj := (гУ+1\гУ+1'))/(ги\ги')') . 7.    Если |г(j+1^| < е, то алгоритм завершается. 8.    Вычислим вектор, вдоль которого вычисляется поправка р^1) := г(J+1') + fyp^. 9.    j: = j+1. 10.    Перейдем к пункту 3.

На основании приведенного алгоритма разработано программное обеспечение на языке C#. Структура программного обеспечения имеет вид

LargeMatrix

SystemResolver

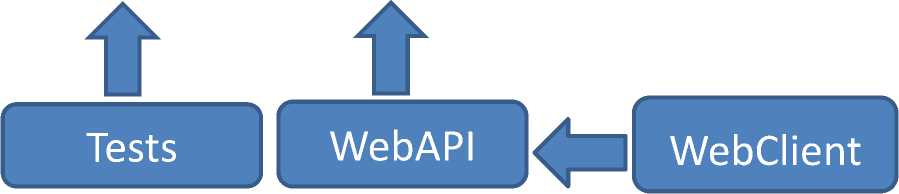
Рис. 1. Структура программного обеспечения.

Опишем модули программного обеспечения.

LargeMatrix – библиотека, содержащая классы разреженной матрицы, плотного вектора и плотной матрицы, а также классов, отвечающих за построение системы уравнений заданного вида.

Tests – модульные тесты, покрывающие библиотеку LargeMatrix, а также метод решения СЛАУ.

SystemResolver – основной проект, содержащий алгоритм решения разреженной системы методом сопряженных градиентов.

WebClient – клиентское приложение, получающее и отображающее данные решения в браузере.

Для хранения разреженной матрицы использовался разреженный строчный формат (Compressed sparse row), который предполагает наличие трех одномерных массивов.

• •    Массив, содержащий все ненулевые элементы матрицы.

• •    Массив, содержащий номера столбцов для соответствующих элементов.

• •    Массив индексов элементов, с которых начинается описание строки.

Вычислительный эксперимент проводился при следующих начальных данных:

N = 10, 01 = -1, 02 = 1, 03= -0.5, 04 = 0.5, h = column(100,150).

Значения x. и x _{; 2} ( i = 1, 10) приведены в таблице 1.

Таблица 1

Значения x jU x ₂, i = 1, 10

i	1	2	3	4	5	6	7	8	9	10
x i ,1	110	190	200	333	355	383	400	415	420	445
x i ,2	151	163	175	204	222	244	266	333	355	380

Результаты вычислительного эксперимента при различных значениях погрешности вычислений £ и параметра Т приведены в таблице 2.

Таблица 2

Количество итераций и время вычислений при различных s и Т

Погрешность, ε	т = 0.5	т = 0.1	т = 0.05	т = 0.01
0.1	32 0,003185 сек.	27 0,003003 сек.	25 0,002839 сек.	24 0,003031 сек.
0.01	33 0,003587 сек.	27 0,003042 сек.	25 0,003219 сек.	24 0,003095 сек.
0.001	33 0,004341 сек.	30 0,003109 сек.	30 0,003307 сек.	24 0,003372 сек.

Анализ таблицы 2 показывает, что при уменьшении параметра Т количество итераций, требуемых для достижения заданной точности ε , уменьшается, и, следовательно, скорость сходимости итерационного метода увеличивается. Вместе с тем, при фиксированном значении параметра Т и уменьшении погрешности вычислений s время вычислений и количество итераций увеличивается незначительно.