Алгоритм решения задачи оптимального трассирования лесовозной автомобильной дороги на неоднородной местности

Будем рассматривать сетку цифровой модели местности (ЦММ), описывающую некоторый прямоугольный участок местности, в виде сильного связанного графа G , вершинами которого являются вершины квадратов сетки, а ребрами – стороны и диагонали этих квадратов [1, 2].

Пронумеровав вершины прямоугольной сетки матричным способом («строки» от 1 до N, «столбцы» от 1 до М), свяжем с графом G прямоугольную систему координат. Вершина, стоящая в i-й «строке» и j-м «столбце» будем иметь координаты (i и j) и обозначатся Vij. Дугу, ведущую из вершины Vij и Vi’j’, обозначим через Uiij'j'. Каждой дуге Uiij'j'графа G поставлено в соответствие неотрицательное число ñiij'j'= с (Uj ), именуемое ценой дуги. Связь цены дуги с введенными выше ценами областей и линейных участков неоднородности раскрывается ниже в этом же разделе диссертации. Каждое ребро состоит из двух противоположно направленных дуг Uiij'j'и Uii'jj' (рисунок 1).

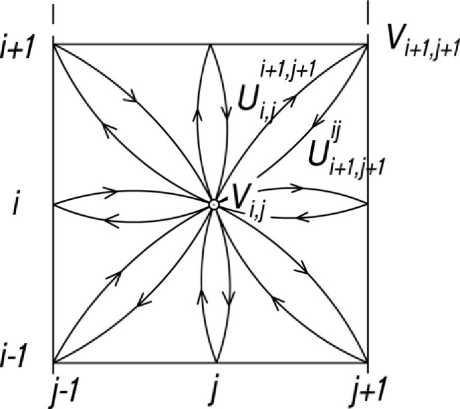
Рисунок 1. Локальная структура сетки ЦММ (графа G ) в окрестности узла V ij

Figure 1. The local structure of the DTM grid (graph G ) in the neighborhood of the node Vij

Путем ^i-j i0j0 шину Vij будем последовательность

из вершины Vij в вер-называть упорядоченную дуг, у которых начало по- следующей совпадает с концом предыдущей: uMt ={ Uij , U‘2-j2 .„, Ui-1j-1 , U‘j }.

0 j 0 0 j 0 i 1 ^j 1 i t - 2 J t - 2 i t - 1 j t - 1

Определим цену пути как сумму цен входящих в него дуг. Классическая задача о кратчайшем пути между двумя вершинами V _ij и V _ij эквивалентна в наших обозначениях задаче поиска пути p ij , имеющего минимальную цену.

Одна из эффективных модификаций метода решения этой задачи состоит в следующем [3]:

• 1.    Вершине V _ij приписывается значение À _ij = 0, остальным вершинам графа А ij =+∞.

• 2.    Просматриваются вершины графа, причем, если найдется такая вершина V ij и ведущая в нее дуга U _i ⁱ _' ^j _{j '} , что А ij > А i’j ’ + ñ _i ^ij _{' j '} , то этой вершине приписывается новое (меньшее) значение А ij = А i’ j ’ + ñ _i ^ij _{' j '} .

• 3.    После того, как все А ij стабилизируется, восстанавливается оптимальный путь ц , начиная с его конца – вершины V _ij . Из п. 2 следует, что найдется такая дуга U ^ikjk , что À = А ij + ñ ^ij .

ij i _k j _k ij

По вершине V ij определяется вершина U i’ j ’ такая, что А ij = А i ’ j ’ + ñ _i ^ij _{' j '} и так далее до начальной вершины пути V _ij

Строгая положительность цен ñ _i ⁱ _j ^{' j '} гарантирует сходимость итерационного процесса и отсутствие замкнутых циклов.

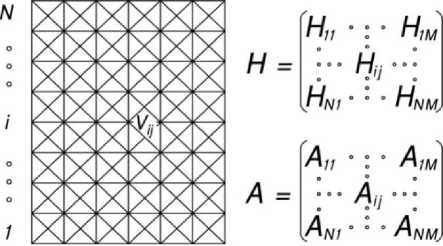
Массивы относительных высот H и значений критерия А вершинах графа G , будем записывать в виде двух матриц из N строк и М столбов (рисунок 2) . Будем также различать грузовое и не грузовое (порожнее) направления движения по трассируемому отрезку лесовозной автомобильной дороги: если в пункт, соответствующий начальной точке V _ij искомого пути на графе G , лесоматериалы ввозятся, то будем говорить, что «задано грузовое направление», если же вывозится, то – «задано не грузовое направление».

ООО / ООО

Рисунок 2. Цифровая модель местности и соответствующие ей матрицы относительных высот Н и критерия оптимальности А

Figure 2. The digital model of the site and the corresponding matrices of relative heights H and the optimality criterion A

На продольные уклоны пути наложены ограничения в виде тангенсов предельно допустимых углов дифференцированно по направлениям: i r – в грузовом, i n – в не грузовом.

В общем виде оптимальный путь ищется на некотором подмножестве Е { N 1 , N 2 , М 1 , М 2 } = { V ij |1 ≤ N 1 ≤ i ≤ N 2 ≤ N , 1 ≤ М 1 ≤ i ≤ М 2 ≤ М }.

В частности, глобальная ЦММ в этих обозначениях запишется как Е{1, N, 1, М}. В матрицах А и Н множеству Е{N1, N2, М1, М2} i = N, j = M соответствует блоки {Аij}    22, {Нij} i = Ni, j = M i i = N2, j = M 2

.

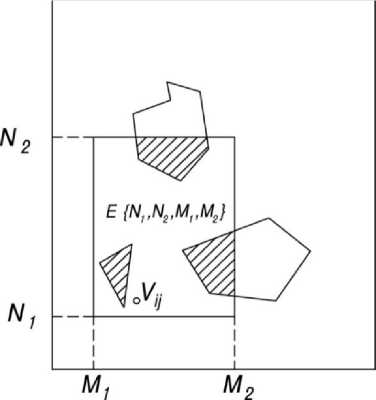
Рисунок 3. Локализация участка поиска оптимального варианта трассы

Figure 3. Localization of a site of search of an optimum variant of a line

Исходное множество Е{N1, N2, М1, М2} разбивается прямыми, проходящими через начальную точку Vij параллельно осям координат, на четыре квадранта (рисунок 4), каждый из которых просматривается в последовательности:

I квадрат – справа налево, снизу вверх, II квадрат – слева направо, снизу вверх, III квадрат – справа налево, сверху вниз, IV квадрат – слева направо, сверху вниз.

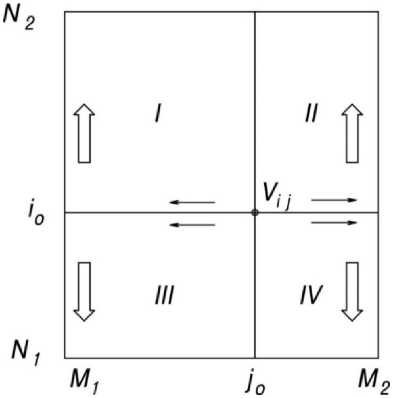
Рисунок 4. Порядок просмотра вершин множества

Figure 4. The order of viewing the vertices of the set

Например, для I квадрата последовательность просматриваемых вершин в координатной записи будет такой (отождествляем вершину с парой ее координат):

( i о , j о - 1 ) ( i o , j о — 2 ) - ( i о , М i + 1).

( j 0 ⁺ 1, j 0 )( i 0 ⁺ 1, j 0 ^{- 1} ) ^x

x ( i 0 + 1, j 0 - 2 ) _ ( i 0 + 1, М 1 + 1).

( N 2 - 1, j 0 )( N 2 - 1, j 0 - 1) x

x ( N 2 - 1, j 0 - 2) _ ( N 2 - 1, М 1 + 1).

Не просматриваются вершины V _ij и вершины, окаймляющие Е { N 1 , N 2 , М 1 , М 2 }, (т. е. имеющие первую координату N 1 или N 2 , либо вторую М 1 или М 2 ).

Исключение из просмотра граничных вершин множества Е { N 1 , N 2 , М 1 , М 2 } обусловлено двумя причинами. Первая – это единство процедуры просмотра и компактный вид программы для ЭВМ. Вторая, более важная причина, заключается возможность локализовать зону поиска оптимума, задавая, например, «отвесные стенки», приписывая граничными вершинами «бесконечные» высоты Н ij .

Это гарантирует замкнутость множества Е : «натыкаясь на стенку», путь не выйдет за пределы Е , поиск в этом случае ведется в глубокой «потенциальной яме» (рисунок 5) . Кстати, таким же образом можно вписать участок местности любой конфигурации в прямоугольную сетку ЦММ.

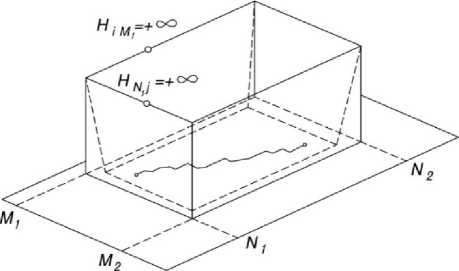
Рисунок 5. Локализация области поиска «отвесными стенками»

Figure 5. Localization of the search area by “sheer walls”

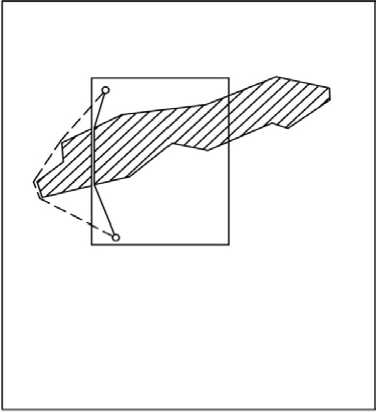
Размеры локализуемого участка зависят от топографии местности и должны определяться с учетом особенностей конкретной моделируемой территории – степени влияния удаленных объектов на положение трассы дороги, вытянутости отдельных складок местности и прочих факторов, которые могут «замаскировать» некоторые оптимальные пути и натолкнуть на ложный вариант. В качестве иллюстраций к высказанным предостережениям приведем пример участка местности с «вытянутым хребтом» (рисунок 6) . Разумеется, от подобных «рифов» не застрахован и глобальный прямоугольник Е {1, N , 1, M }, поэтому моделированию конкретного участка местности должен предшествовать содержательный анализ ситуации.

Просмотр одной вершины V ij включает в себя последовательный перебор 8-ми входящих в эту вершину дуг U^ 1, j - 1 , U ^j 1, j _ U j - 1 , для которых определяются их цены ñ _i ^ij _{' j '} и значения критерия полагается равным A ij = min ij ( A ij + c ij , ) .

При определении цены дуги ñ _i ^ij _{' j '} могут встретиться три случая.

Первый случай . Уклон превышает допустимый. Цена дуги полагается равной очень большому числу: ñ _i ^ij _{' j '} =+∞

Тангенс допустимого угла наклона α дуги U _i ⁱ _' ^j _{j '} , должен находиться в пределах:

• - i r <  tg a <  i n - если заданное грузовое направление

• - i n <  tg a <  i r - если заданное не грузовое

направление.

tg « =

а

где а = диагональ квадрата сетки, если i - i’ +1 j - j’ = 2 сторона квадрата сетки в остальных случаях

м, м₂

Рисунок 6. Пример маскировки истинного оптимального пути при ошибочной локализации области поиска оптимума:            – истинный оптимальный путь,            – ложный

Figure 6. Example of masking the true optimal path for an erroneous localization of the search area of the optimum:                – the true optimal way,

– false

Второй случай. Дуга Uii'jj', имеет допустимый уклон и принадлежит области неоднородности Dτ. ñiij'j'= сτ*lii'jj', где ст - цена области Dт; Ij, =. /(н - н,,)2 + a2. j     ijij

Дуга U _i ⁱ _' ^j _{j '} принадлежит D τ тогда и только тогда, когда обе вершины V ij и V i,j , принадлежит D т .

Факт принадлежности точки выпуклой области, ограниченной отрезкам прямых, устанавливается средствами векторного анализа.

Пусть на плоскости π с положительно ориентированной системой координат хОу задана выпуклая область D с кусочно-линейной границей σD. Граничные точки соединения отрезков перенумеруем по часовой стрелке, начиная с любой: А1, А2…, Ак.

Вектор с началом в точке А и концом в точке В будем обозначать АА .

Пусть В – произвольная точка плоскости π. Чтобы В принадлежала области D необходимо и достаточно, чтобы одновременно выполнялись неравенства:

• [ АВ , , а а ;:; ] _z >  о, \ _ a^, A_t A i ] _z >  о , (1)

i = 1,2…, к-1

Здесь квадратные скобки означают векторное произведение, а индекс z единственную отличную от нуля координату векторного произведения двух векторов, лежащих в одной плоскости. Доказательство очевидно.

Таким образом, принадлежность точки (вершины квадрата сетки ЦМР) области неоднородности D τ устанавливается последовательной проверкой справедливости неравенств (1).

Если хотя бы одно из них не выполняется, то точка лежит вне области. Как известно, третья координата векторного произведения двух векторов à = (а х , а у , О), b = (b х , b у , О) очень просто выражается через координаты этих векторов: [ à , b ] z = а х *b у – а у *b х , что обеспечивает высокую эффективность и быстродействие описанного способа определения взаимного положения точки и области.

Третий случай . Дуга U _i ⁱ _' ^j _{j '} имеет допустимый уклон, принадлежит области неоднородности D τ и пересекается с линейным участком неоднородности, имеющим цену с р .

В этом случае цена дуги определяется так: ñ _i ^ij _{' j '} = с τ * l _i ⁱ _' ^j _{j '} + с р .

Факт пересечения дуги с линейным участком неоднородности устанавливается следующим образом. Сначала выясняется принадлежность обеих концевых точек дуги одному из прямоугольников Р к , построенных на отрезках ломаной линии, описывающей данный участок неоднородности (рисунок 7) . Если найдется такой прямоугольник, то определяется факт пересечения дуги с его диагональю – отрезком ломаной.

Учитывая необходимость многократного определения факта принадлежности точки прямоугольным множеством на плоскости в процессе решения задачи оптимального трассирования, вычислительным аспектам этого вопроса было уделено особое внимание. Для повышения эффективности указанной процедуры разработан специальный аппарат так называемых вложенных сит [8, 9].

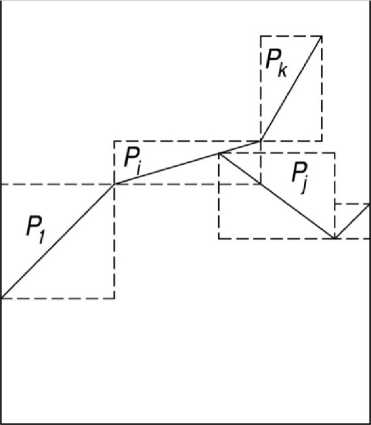
Рисунок 7. Определение дуг, пересекающихся с линейными участками неоднородности

Figure 7. Definition of arcs intersecting linear regions of heterogeneity

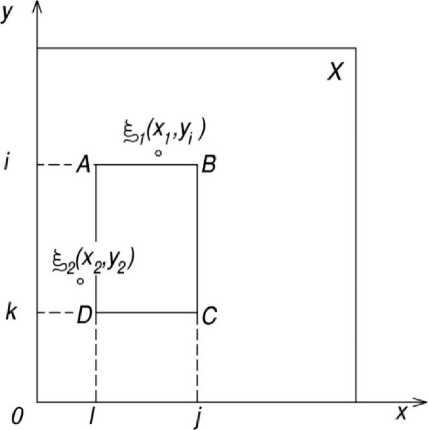
Рисунок 8. К методу вложенных сит определение дуг, пересекающихся с линейными участками неоднородности Figure 8. To the method of embedded sieves, the definition of arcs intersecting linear regions of the inhomogeneity

Сущность его заключается в определении оптимальной по быстродействию последовательности сравнений координат ( x , у ) произвольной точки ξ( x , у ) на плоскости с координатами системы прямоугольников для установления факта принадлежности этой точки одному из прямоугольников системы.

Основную идею поясним на примере одного прямоугольника АВСD со сторонами, параллельными осями координат хОу (рисуно к 8) . Точки ξ( x , у ) будем считать принадлежащими некоторому объемлющему прямоугольник АВСD прямоугольнику Х (аналог глобальной ЦММ). Уравнения сторон прямоугольника АВСD , соответственно, равны:

АВ : у = i , ВС : x = j , СD : у = k , АD : x = l.

Точка ξ( x , у ) принадлежит прямоугольнику АВСD тогда и только тогда, когда одновременно выполняются четыре неравенства:

x ≥ l, x ≤ j , у ≥ k , у ≤ i . (2)

На суммарное количество сравнений, которое потребуется выполнить для точек, не принадлежащих прямоугольнику АВСD (для каждой принадлежащей АВСD точки ξ таких сравнений будет, очевидно, оказывают влияние два фактора:

─ порядок проверки справедливости неравенств (2),

─ расположение прямоугольника АВСD относительно объемлющего его множества Х и параметры их обоих.

Действительно, если априори принять последовательность проверки неравенств (2) в том порядке, в каком они записаны выше, то для определения того, что точка ξ 1 ( х 1 , у 1 ) на рисунке 8 не принадлежит прямоугольнику АВСD , понадобится четыре сравнения, т. к. только последнее неравенство окажется невыполненным ( у 1 >  i ). Для точки же ξ 2 ( х 2 , у 2 ) потребуется всего лишь одно сравнение ( x < l).

Для системы из n прямоугольников ситуация существенно усложняется. Выбор неоптимальной последовательности сравнений (2) повышает трудоемкость процесса перебора точек множества Х (узлов сетки ЦММ) примерно в 1,5 раза.

При постоянных коэффициентов z 0 и z 1 , входящих в выражение (1), цены областей неоднородности с i являются сложными функциями продольного уклона пути i , от которого зависит скорость движения автопоезда V( i ).

Скорость движения лесовозного автопоезда, учитывая кусочно-линейный продольный профиль трассы дороги, определялась методом равновесных скоростей [10].

Величина полного сопротивления движению автопоезда ΣW, Н с учетом сопротивления воздушной среды принимались по формуле:

2 W = Q 6p ( го ± i c ), (3) где Q бр – масса автопоезда (тягача с роспуском или прицепом) брутто, т; ω – основное удельное сопротивление движение автопоезда, включая сопротивление воздушной среды, Н /т; i с – сопротивление от уклона пути, Н /т (+ для подъема, – для спуска); i с = 9,81 ⋅ i , где i – уклон пути, %.

Согласно рекомендациям [5] для лесовозных автомобильных дорог с покрытиями переходного типа (магистрали и ветки) и средних условий эксплуатации можно принимать:

го = 166,7 + 3,4-V, где V – скорость движения автопоезда, км/ч.

Подставляя выражение для основного удельного сопротивления движению в формулу (3) для автопоезда КАМАЗ-43118 + ПРЛ11-КБ УСТ-94651, например получим дифференцированно по направлениям – грузовому и порожнему – следующие зависимости величины полного сопротивления движению от скорости и уклона:

В грузовом направлении:

S W = 39,7 x ( 166,7 + 3,4 V ± i - ) =

= 6618.0 + 136.3xV± 39.7iR в порожнем направлении: (3)

S W = 16,7 - ( 166,7 + 3,4 V ± i - ) =

= 2783,9 + 56,8 - V ± 16,7 i ,

Графики зависимостей (3) для различных уклонов пути i с шагом Δi = 5% наносились на график тяговой характеристики тягача КАМАЗ-43118, построенный по данным [5].

Определенные графически значения равновесных скоростей сведены в таблице 1, по ре-

Для автоматизации расчета скорости движения автопоезда и вывода компактной формулы t = t ( i ) функция t = ¹ сглаживалась полиномами 2-й и 4-й степени. Коэффициенты полиномов определялись методом наименьших квадратов. Для указанного выше типа автопоезда были получены следующие зависимости:

в грузовом направлении:

t = (290.51597 + 6.13928 i + 0.03876 i ² )10 — 4 ,

(    293.23210 + 10.83532i +)

t =

(+0.01014i2 -0.00587i3 + 0.00008i4 J в порожнем направлении:

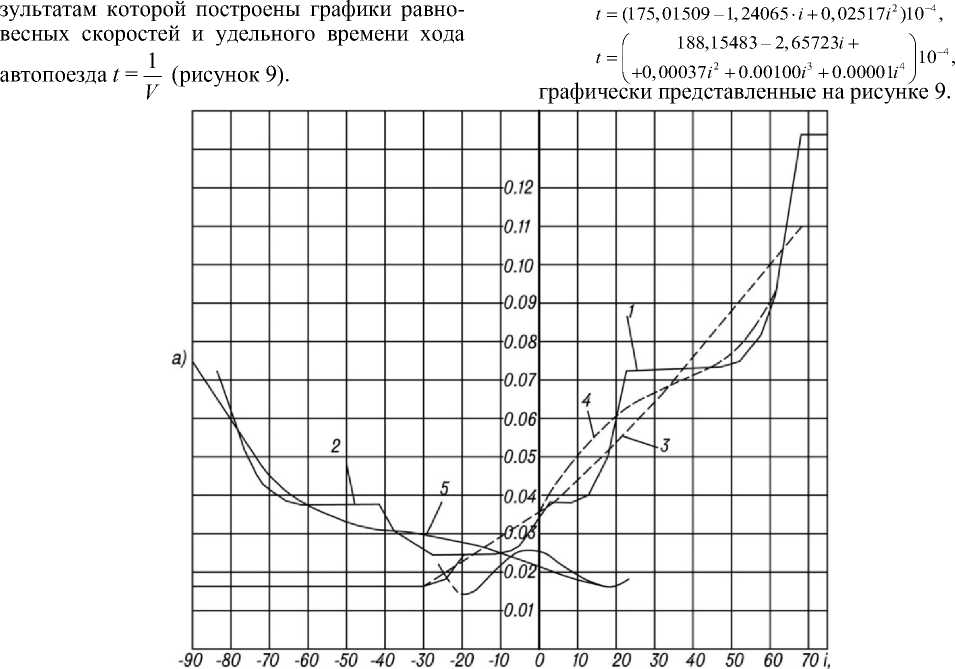
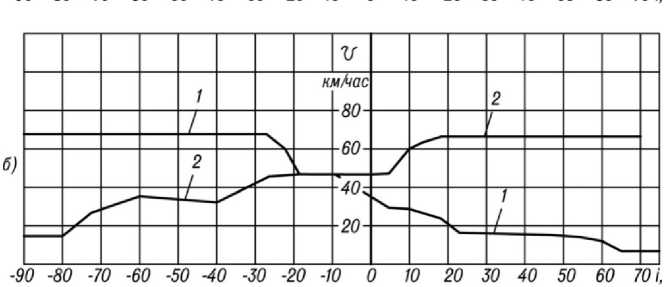
Рисунок 9. Зависимость темпа роста к скорости движения автопоезда от продольного уклона дороги: а) графики темпа движения; б) графики скорости движения; 1-для грузового направления; 2 – для порожнего направления; 3 – сглаживание полиномом 2 степени (грузовое направление.); 4 – сглаживание полиномом 4 степени (груз. напр.); 5 – то же полиномом 7 степени (пер.)

Figure 9. Dependence of the rate of growth on the speed of the road train from the longitudinal slope of the road: a) graphs of the rate of movement; B) speed charts; 1-for the freight direction; 2 – for empty direction; 3 – smoothing by a polynomial of the 2nd degree (freight direction.); 4-smoothing by a polynomial of 4 degrees (load eg); 5 – the same polynomial of degree 7 (trans)

Эффективность использования зависимости t = t ( i ) в табличном виде (таблица 1) или в виде формул (4) определяется характером моделируемого рельефа, необходимой точностью расчетов. Если продольные уклоны трассы преимущественно находятся в интервалах i ≤ 10%, i ≥ 35%. Табличный вид задания t ( i ) требует большего объема оперативной памяти компьютера и в среднем увеличивается время расчетов по сравнению с формулами (4) обеспечивает компактный вид записи функции и экономию ресурса компьютера, но в среднем приводит к менее точным результатам. В программном обеспечении описываемой модели (1) предусмотрены все три варианта задания функции t ( i ), выбор одного из них осуществляется на этапе настройки системы программ.

Поскольку двигатели лесовозных автопоездов эксплуатируются, как правило, в режиме дросселирования (на частичных характеристиках), а равновесные скорости определяются по внешним характеристикам двигателя, то для перехода от расчетных скоростей к действительным скоростям движения автопоезда используется коэффициент 0,87, полученный экспериментальным путем исследователями [2, 4].

После того как на р-й итерации просмотрены все вершины множества Е{N1, N2, М1, М2} подсчитывается сумма всех значений критерия в вершинах i=N 2

j = M 2

S p = 2 A , i = N 1 j = M 1

Процесс изменения значений A ij заканчивается, когда два последовательных числа S k и S k+ 1 совпадут

S 1 > S 2 >_> S k = S k _{+ 1} =           (5)

Значение k – общее количество итераций до стабилизации матрицы критерия – характеризует сходимость алгоритма и зависит от конкретной задачи – сложность рельефа, численности, конфигураций и взаимного расположения областей и линейных участков неоднородности. При решении практических задач трассирования лесовозных автомобильных дорог на реальных территориях k варьировалось от 2 до 16, хотя при искусственно моделируемых ситуациях в период отладочных работ значение k достигало 25–27.

В процессе работы блока оптимизации выполняется аппроксимация эскизной линии элементами трассы в пределах первоначально заданной последовательности, то есть меняются только величины геометрических характеристик элементов, но не их количество и тип. Вместе с тем независимо от способа формирования исходного приближения, довольно часто появляется необходимость просматривать варианты проектируемой трассы, отличающиеся последовательностью элементов.

Таблица 1.

Зависимость скорости движения автопоезда КАМАЗ-43118 + ПРЛ11-КБ УСТ-94651 от продольного уклона гравийной дороги

Table 1.

Dependence of the speed of the KAMAZ-43118 + РRL11-KB road UST-94651 on the longitudinal slope of the gravel road

Продольный уклон, %	Направление движения автопоезда
	грузовое		порожнее
	Скорость, км/ч	Темп, ч/км	Скорость, км/ч	Темп, ч/км
-30	71,1	0,0141	71,1	0,0141
-25	64,0	0,0156	71,1	0,0141
-20	47,1	0,0212	71,1	0,0141
-15	47,1	0,0212	67,6	0,0148
-10	47,1	0,0212	60,0	0,0167
-5	44,2	0,0226	50,0	0,0200
0	36,0	0,0278	47,1	0,0212
5	31,0	0,0323	47,1	0,0212
10	31,0	0,0323	47,1	0,0212
15	29,2	0,0342	47,1	0,0212
20	24,0	0,0417	47,1	0,0212
25	16,25	0,0615	47,1	0,0212
30	16,25	0,0615	47,1	0,0212
35	16,25	0,0615	42,4	0,0236
40	16,25	0,0615	37,7	0,0265
45	16,25	0,0615	31,0	0,0323
50	16,25	0,0615	31,0	0,0323
55	16,0	0,0625	31,0	0,0323
60	14,7	0,0680	31,0	0,0323
65	12,5	0,0800	31,0	0,0323
70	8,98	0,1114	30,6	0,0327
75	8,98	0,1114	28,4	0,0352
80	8,98	0,1114	25,6	0,0391
85	8,98	0,1114	21,4	0,0467
90	8,98	0,1114	16,25	0,0615

Последовательности (5) соответствует последовательность матриц критерия А 1 , А 2 … А k = А k+1 =…

Символически процесс стабилизации матрицы А критерия можно представить в виде последовательности воздействия на А некоторого оператора ζ:

Ар = ζ(Ар-1), р = 2,3…, k + 1, где А1 имеет специальный вид: Àij = О, Аij =+∞ для всех (i, j) ≠ ( i0 , j0).

А к+1 в этих обозначениях запишется: А к + 1 = ζ (А к ) = ζ (ζ(А к-1 ))=… ζ^к(А 1 ).

Оператор ζ зависит от точки V _ij и процедуры определения цен дуг графа G . Для заданной ЦММ при фиксированном типе транспортных средств на вывозке и дорожного покрытия цены определяются автоматически в зависимости от объема вывозимой древесины Q и направления грузового движения τ (τ – задано грузовое направление, τ – негрузовое). С учетом этого можно записать:

А к+ 1 =[ζ( V _{i 0 j 0} , Q , τ)] ^k ( А 1 ) (6)

Такая символическая форма записи решения задачи о нахождении оптимального варианта лесовозной автомобильной дороги для вывозки сосредоточенного объема древесины поможет в дальнейшем создать пакет программ.