Алгоритм решения задачи оптимального управления химико-технологическим процессом с терминальными ограничениями

Основная задача промышленного предприятия состоит в максимально эффективном использовании имеющихся ресурсов с минимальными издержками производства. Решить данную проблему можно путем применения цифровых двойников химико-технологических процессов. Это позволит смоделировать работу технологической установки или конкретный химико-технологический процесс.

Поэтому возникает необходимость в установлении тесной связи производства и научных организаций для создания новых цифровых технологий и решения ряда задач по оптимизации и модернизации, в частности определения оптимальных параметров проведения химико-технологических процессов в различных условиях.

Задачу определения оптимальных режимных параметров ведения химико-технологических процессов можно решить путем применения методов математического моделирования. Для ее формализации необходимо составить математическую модель процесса (например в виде системы дифференциальных уравнений), выделить управляющие параметры и область их изменения, а также обозначить критерий качества управления. В задачах оптимального управления ограничения могут быть наложены не только на управляющие параметры, но и на фазо- вые переменные. Если ограничения на фазовые переменные заданы в конечный момент времени функционирования системы, то такая задача является задачей с терминальными ограничениями [1]. Разработка численных методов решения задачи оптимального управления с терминальными ограничениями представляет научный и практический интерес, поскольку более сложные задачи с фазовыми и промежуточными ограничениями могут быть сведены к терминальным задачам путем применения математических редукций [2].

Цель работы - разработка численного алгоритма решения задачи оптимального управления химико-технологическим процессом с терминальными ограничениями.

Обзор литературы

Для решения задач оптимального управления с фазовыми ограничениями существует несколько подходов. Один из них предполагает вывод точных условий оптимальности и исследование свойств получаемых решений [3; 4]. Необходимые условия оптимальности решений задач оптимального управления с фазовыми ограничениями в форме принципа максимума Понтрягина получены как в работах российских авторов [5; 6], так и в зарубежных исследованиях [7; 8]. Однако при разработке численных алгоритмов решения задач оптимального управления данный подход трудно реализовать на практике.

Другой подход основан на применении метода штрафов для практической реализации алгоритмов решения задачи оптимального управления с ограничениями, наложенными на фазовые переменные. Основная идея метода штрафов заключается в замене задачи с фазовыми ограничениями на задачу без ограничений путем добавления «штрафа» к критерию оптимальности. При этом последовательность решений новой задачи оптимального управления дает решение исходной задачи.

Разработке методов решения задач оптимального управления с терминальными ограничениями на основе метода штрафа посвящен ряд работ [9–13]. Численная реализация данного метода представлена в работах, в которых последовательность оптимизационных задач без ограничений решается с помощью градиентного метода [14; 15]. Однако недостатком градиентных методов является чувствительность решения оптимизационной задачи к выбору начального приближения, что может привести к попаданию решения в локальный экстремум или в область, противоречащую физическому смыслу задачи.

Основные трудности, возникающие при программной реализации методов решения задач оптимального управления, связаны с нелинейностью описания процесса, высокой размерностью пространства поиска, наличием фазовых ограничений, а также чувствительностью найденного решения к начальной точке поиска [16; 17]. Преодолеть перечисленные трудности позволяет применение эволюционных методов оптимизации, к которым относится метод искусственных иммунных систем.

Метод искусственных иммунных систем основан на имитации функционирования иммунной системы живых организмов. Функционирование заключается в защите от неблагоприят- ных внешних воздействий (патогенов, антигенов) [18–20]. В этом процессе основную роль играют защитные клетки – антитела, вырабатываемые иммунными клетками и претерпевающие изменения в ходе борьбы с антигенами и патогенами. Наиболее приспособленные для защиты антитела подавляют чужеродные тела, и именно эти клетки запоминает иммунная система для их воспроизведения при повторной атаке организма схожим патогеном.

В настоящее время искусственные иммунные системы находят широкое применение при решении задач распознавания образов [21], прогнозирования [22], классификации [23], оптимизации [24] и оптимального управления [25].

По сравнению с классическими методами оптимизации метод искусственных иммунных систем обладает рядом преимуществ, к которым можно отнести независимость найденного решения оптимизационной задачи от начального приближения. Отсутствие чувствительности решения задачи к начальному приближению достигается за счет того, что в начале поиска задается набор векторов возможных решений, которые заполняются случайными допустимыми значениями и в ходе работы алгоритма путем применения операторов метода претерпевают изменения, приближаясь к решению оптимизационной задачи. По сравнению с другими эволюционными методами искусственные иммунные системы оперируют в своей работе лучшими решениями, найденными на предыдущей итерации поиска, что позволяет применять их при решении задач мультимодальной оптимизации [26].

В настоящей работе представлен пошаговый алгоритм для поиска численного решения задачи оптимального управления химико-технологическим процессом с терминальными ограничениями и его апробация на модельном примере.

Материалы и методы

Пусть динамика протекания химико-технологического процесса описы- вается системой обыкновенных ференциальных уравнений dX = f (x (t), u (t), t)

dt

диф-

с начальными условиями x (0) = X0,              (2)

где x ( t ) = ( x 1 ( t ), x 2 ( t ),..., x n ( t )) T - вектор фазовых переменных; u ( t ) e U -параметр управления; U - множество допустимых значений управления; t e [0, 1 1 ] - время, f ( x ( t ), u ( t ), t ) = ( f(t), u(t), t),f.(x(t), u(t), t), ...,f(x(t), u(t), t))T-вектор-функция, непрерывная вместе со своими частными производными [27].

Пусть множество U задается неравенством

U a <  U ( t ) <  U b ,             ⁽³⁾

где u a , u b - верхняя и нижняя допустимые границы значений параметра управления.

Пусть на фазовые переменные в момент времени t ₁ наложены ограничения:

r j ⁽ x ⁽ t 1 )) = 0, j = 1, m,       ⁽⁴⁾

r j ( x ( 1 1 )) <  0, j = m + 1, p, (5) где r j ( x ) - непрерывно дифференцируемые функции.

Введем функционал качества управления:

R ( u ) = r ₀( x ( 1 1 )) ^ min.      (6)

Требуется для химико-технологического процесса, описываемого системой дифференциальных уравнений (1) с начальными условиями (2), найти та- кую управляющую функцию u* (t) e U, с учетом ограничений (4), (5), для которой критерий оптимальности (6) принимает минимальное значение.

Для решения задачи оптимального управления (1)–(6) применим метод штрафов и метод искусственных иммунных систем.

Для того чтобы применить метод штрафов, необходимо построить новый критерий оптимальности, содержащий штрафной функционал W ( u , S k ), значение которого равно нулю при выполнении ограничений (4), (5) и больше нуля в противном случае. Поэтому введем в рассмотрение критерий оптимальности

P(u ) = R(u ) + W(u , s ^k ) ^ min, (7)

где W ( u , s^k ) - штрафной функционал, определяемый по формуле

W(u,sk) = sk (m                p                       ^

⁼ vl E l r j (x(1 1 ) I^{2 +} E (max(0, r , ( x(1 1 ))))² I ,

² ^ j = 1                   j = m + 1                          )

где k – номер итерации, s^k – параметр штрафа.

На каждой итерации поиска решения необходимо найти решение задачи оптимального управления без ограничений. Найденный параметр управления u * ( t ) становится начальным для следующей итерации с увеличенным значением параметра штрафа.

Последовательность решений задачи оптимального управления (1)–(3), (7) дает решение исходной задачи (1)–(6).

Для решения задачи оптимального управления (1)-(3), (7) применим метод искусственных иммунных систем. Критерий оптимальности (7) соответствует понятию приспособленности иммунной клетки к борьбе с антигенами и патогенами и представляет собой фитнес-функцию. Пусть иммунной клеткой является вектор управляющих параметров и = (и 1, и2, .., U)), а набор из count_u таких векторов составляет популяцию

u‘ = (ui,u2,...,u‘i), i = 1,count_u. (8)

Наиболее приспособленной иммунной клетке и соответствует наименьшее значение фитнес-функции (7), так как решается задача на поиск минимума критерия оптимальности.

Результаты исследования

Сформулируем численный алгоритм решения задачи оптимального управления с терминальными ограничениями, основанный на комбинации метода штрафов и метода искусственных иммунных систем:

• 1.    Задать параметры алгоритма искусственных иммунных систем: начальное значение параметра штрафа s ⁰, размер популяции count_u , количество иммунных клеток с наихудшим значением фитнес-функции maxf, количество клеток-родителей для селекции sel , количество клонов для оператора клонирования klon , параметр оператора мутации mut , параметры завершения поиска решения ε ₁, ε ₂.

• 2.    Случайным образом заполнить начальную популяцию иммунных клеток (8) допустимыми значениями из области U .

• 3.    Вычислить значение фитнес-функции (7) для ка ждой иммунной клетки и, , i = 1, count _ u .

• 4.    Применить к текущей популяции оператор клонирования. Для этого выбрать наиболее приспособленные иммунные клетки (клетки-родители) и создать для каждой klon копий.

• 5.    Применить к каждому вектору-клону оператор мутации. Для этого сгенерировать случайные числа q 1 е [0, U b - u i ], q ₂ е [0, u i - U a ], q 3 e [0,1] для каждой клетки-родителя. Координаты клона вычислить по формуле [28]:

  u mⁱ ut

  
  

  <

  
  

• 6.    Вычислить значение фитнес-функции (7) для каждой клетки-мутанта.

• 7.    Применить к каждому клону-мутанту оператор селекции. Для этого выбрать среди них наиболее приспособленные клетки и поместить в популяцию вместо клетки-родителя при условии, что она менее приспособлена по сравнению с клоном-мутантом.

• 8.    Случайным образом сгенерировать maxf новых иммунныx клеток и вычислить для них значение фитнес-функции.

• 9.    Выбрать из популяции maxf наименее приспособленные иммунные клетки и заменить их новыми клетками.

• 10.    Проверить условие окончания поиска решения задачи оптимального управления без ограничений. Если изменение значения фитнес-функции не превышает заданной малой величины ε ₁, то выбрать из последней популяции клетку и * с наименьшим значением фитнес-функции, иначе перейти к шагу 4.

• 11.    Проверить условие окончания работы алгоритма. Если W ( и * , s^k ) >  S ₂, то увеличить штраф по правилу:

ui + q 1 • mut, q3 > 0,5, ui - q2 • mut, q3 < 0,5.

sk+1 = 10 • sk.

В качестве начальной популяции для следующей итерации алгоритма задать наиболее приспособленную иммунную клетку и *. Затем перейти к шагу 4.

Если W(u * , s k ) <  е ₂, то остановить работу алгоритма. Решением задачи оптимального управления будет наиболее приспособленная иммунная клетка и * из последней популяции.

Найдем численное решение задачи оптимального управления с терминальными ограничениями с помощью описанного алгоритма.

Пусть химико-технологический процесс описывается системой обыкновенных дифференциальных уравнений

dx 1

„"dt " u’ dx 2 . dt " x ”

<

где x ( t ) = ( x 1 (t ), x ₂( t )) - вектор фазовых переменных; u ( t ) - параметр управления; t e [0,1] - время функционирования системы.

Область допустимых значений параметра управления задается неравенством:

|u(t)| < 1.(10)

Пусть заданы начальные значения фазовых переменных:

x 1(0) = x 2(0) = 0.(11)

На значение фазовой переменной x1 в конечный момент времени наложено ограничение вида x ,(1) = 0.(12)

Пусть критерий оптимальности имеет вид

R(u) = jx2(t)dt ^ min. (13)

Необходимо для химико-технологического процесса, описываемого системой обыкновенных дифференциальных уравнений (9) с начальными условиями (10), найти такое управление u * ( t ), при котором выполнены ограничения (10), (12) и достигается минимум критерия оптимальности (13).

Критерий оптимальности со штрафным функционалом в нашем случае имеет вид

1 k

P ( u ) = j x ₂( t ) dt + — ( x j(1))² ^ min. (14) 0 ² 2 ¹

Для решения поставленной задачи оптимального управления в среде визуального программирования Delphi реализовано программное средство, в основу которого положен разработанный комбинированный алгоритм.

Численное решение системы обыкновенных дифференциальных уравнений (9) с начальными условиями (11) найдено с помощью метода Рунге - Кутты четвертого порядка.

Разработанный алгоритм применен со следующими параметрами: s ⁰ = 0,01, count_u = 40, maxf = 10, se l = 15, klon = 10, mut = 0,5, s 1 = s ₂ = 10^-4.

Врезультате решениязадачи(9)–(13) с помощью разработанного алгоритма определено оптимальное управление u * ( t ) (рис. 1) и соответствующая ему оптимальная траектория процесса (рис. 2). При этом RmAи * ) = - 0,2497, а x 1 (1) = - 2,4 • 10 - 17 .

Для оценки решения задачи (9)-(13), найденного с помощью разработанного комбинированного алгоритма, сравним его с решением, полученным в работе В. А. Срочко с помощью метода игольчатой линеаризации (обозначим его u *L ( t ) ) 1 .

Согласно В. А. Срочко,

uIl (t) =

-1, t e

0,, 2

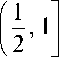
Относительная погрешность рассчитанного вектора оптимального управления u * составила § ( u * ) = 1,9 %, поэтому можно сделать вывод о корректной работе комбинированного

koj ,---------------------

0,8

0,6

0,4

0,2

* S o,O-

-0,2

-0,4

• -0,6 -

  -0,8

• -1,0 -----------------------------'

0,0       0,2       0,4       0,6       0,8       1,0

t

Р и с. 1. Оптимальное управление

F i g. 1. Optimal control

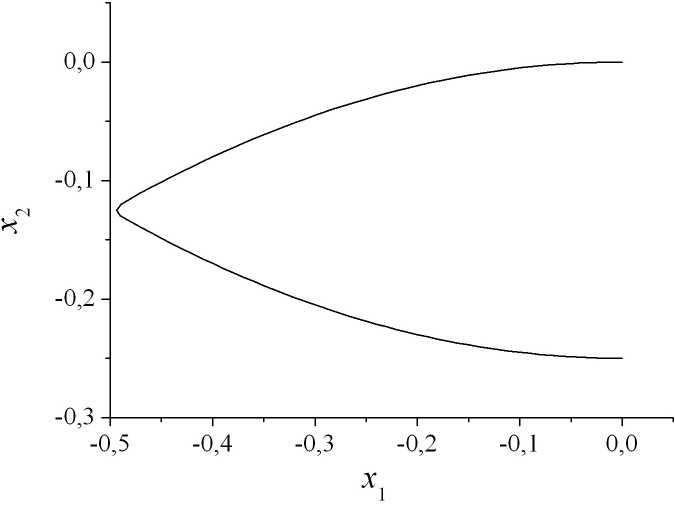
Р и с. 2. Оптимальная траектория процесса

F i g. 2. Optimal process trajectory

алгоритма решения задачи оптимального управления химико-технологическим процессом с терминальными ограничениями.

Обсуждение и заключение

Таким образом, разработанный алгоритм позволяет найти решение задачи оптимального управления химико-технологическим процессом при наличии ограничений на фазовые переменные и на параметр управления. Работа алгоритма основана на применении метода штрафов и метода искусственных иммунных систем. С помощью метода

штрафов исходная задача с терминальными ограничениями сводится к задаче оптимального управления без ограничений, решение которой ищется с помощью метода искусственных иммунных систем. Особенностью разработанного алгоритма решения задачи оптимального управления с терминальными ограничениями является независимость от начальной точки поиска решения.

С помощью алгоритма проведен вычислительный эксперимент для модельной задачи оптимального управления химико-технологическим процессом.

В результате расчетов определены параметры оптимального управления, обеспечивающего достижение минимального значения критерия оптимальности, и соответствующая оптимальная траектория процесса. Приведено

сравнение полученного численного решения модельной задачи с решением, рассчитанным с помощью метода игольчатой линеаризации. Показано, что относительная погрешность найденного решения не превышает 2 %.

418 Технологии, машины и оборудование

Поступила 06.06.2022; одобрена после рецензирования 05.07.2022; принята к публикации 20.07.2022

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

Submitted 06.06.2022; approved after reviewing 05.07.2022; accepted for publication 20.07.2022

All authors have read and approved the final manuscript.