Алгоритм синтеза цифровых фильтров на основе прямого и обратного преобразования Фурье с промежуточной обработкой спектра

Постановка задачи

Развитие цифровых систем обработки сигналов (ЦОС), работающих в реальном времени, связано с эффективностью алгоритмов реализации цифровых фильтров. Основным методом синтеза цифровых фильтров является временной метод, в основе которого лежит свертка текущей выборки отсчетов сигнала и отсчетов импульсной характеристики фильтра. Алгоритмы таких фильтров требуют хранения отсчетов импульсной характе- ристики, которых может быть несколько тысяч, а операция свертки выполняется на каждом интервале дискретизации. Это существенно снижает быстродействие фильтров [1].

Менее исследованным и менее распространенным является частотный метод синтеза цифровых фильтров, в основе которого лежит прямое и обратное дискретное преобразование Фурье (ДПФ) с промежуточным преобразованием спектра. Данный метод может быть использован в реальном времени для текущей выборки отсчетов сигнала, а алгоритмы ДПФ ускорены из-за отсутствия необходимости вычислений всех отсчетов спектра и всех отсчетов восстановленного сигнала.

Основной задачей работы является исследование возможностей частотного метода и синтез соответствующих алгоритмов работы цифровых фильтров.

Алгоритмработыцифровогофильтра

На первом этапе (см. рис. 1) по выбранной длительности окна T и выбранному интервалу дискретизации At формируется текущая выборка отсчетов сигнала, которая в каждом цикле обновляется в результате сдвига окна на один интервал дискретизации. Количество отсчетов T на интервале окна m = — + 1 = 2” для широко А/ используемых алгоритмов ДПФ.

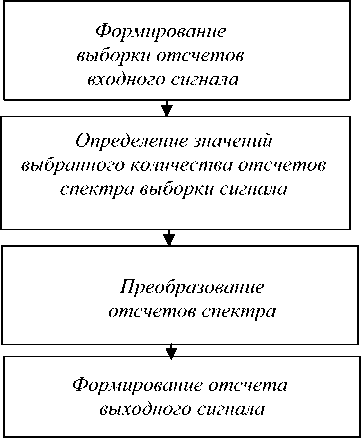
Рис. 1. Структура алгоритма

На четвертом этапе с помощью обратного ДПФ формируется единственный отсчет выходного сигнала, который привязывается к текущему времени. Видно, что алгоритм обратного ДПФ может быть существенно упрощен.

Исследуем свойства фильтра, если в результате преобразования спектра остается только один отсчет первой гармонической составляющей. Найдем АЧХ и ФЧХ фильтра. Для этого используем гармонический входной сигнал с угловой частотой co и единичной амплитудой. С помощью прямого ДПФ найдем спектр текущей выборки отсчетов гармонического сигнала и исключим все составляющие, кроме основной гармонической составляющей. Затем определим значение текущего отсчета выходного сигнала.

Определим с помощью прямого ДПФ значения отсчетов выходного сигнала для одного окна, исходя из того, что в спектре оставлена одна основная гармоническая составляющая:

. In . .

Z/2 = ЛС08 ---- kAt

v mAt

+ В sin

2л" ----kAt v mAt ,

На втором этапе выполняется прямое ДПФ для текущей выборки отсчетов сигнала, предполагая, что выборка сделана на одном периоде некоторого периодического сигнала. Прямое ДПФ дает ограниченный дискретный спектр указанного сигнала.

На третьем этапе выполняется преобразование спектра, например, ограничение количества отсчетов спектра, умножение отсчетов на комплексные коэффициенты и другие возможные преобразования.

где k — номер отсчета выборки сигнала.

Так как выходной сигнал формируется последним отсчетом ( k = m ), то (1) принимает вид:

иТ = — У cos^cokAt + col А?) ■ cos m _k=0

^^kAt , (2) mAt ,

где l – номер шага смещения окна. Воспользуемся табличным интегралом [2] для преобразования (2). В результате получим выражение (3) для l отсчета выходного сигнала:

sin ^colAt^

sin

2л" mAt

.        2л"

2 co +-----

777 A t

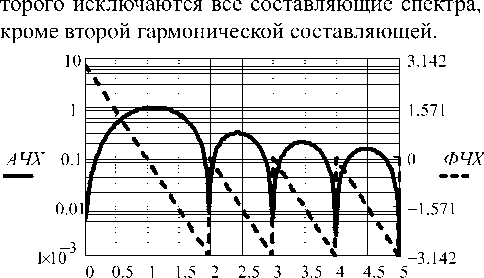
Выражение (3) является математической моделью фильтра. Изменяя частоту входного сигнала и фиксируя l , можно получить АЧХ и ФЧХ. Если зафиксировать частоту входного сигнала, то видно, что частота выходного сигнала при изменении l равна частоте входного сигнала. АЧХ и ФЧХ фильтра приведены на рис. 2, где to_ti =2лТ .

Видно, что АЧХ имеет выраженную полосу пропускания, а ФЧХ имеет линейный характер, что говорит о неискажающих свойствах фильтра. Изменяя ширину окна, можно управлять полосой пропускания фильтра. ФЧХ фильтра привязана к ширине окна.

Рассуждая аналогичным образом, получим математическую модель фильтра, в алгоритме ко-

co to О

Рис. 2. Частотные характеристики фильтра первой гармоники sin

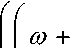
m\t

■mM+ co I At

sin (t)

sin

4^ о н-- mAt

T ro -

Ал

mAt

_ Ал

2 (у +----- m^t

Графики АЧХ и ФЧХ фильтра приведены на

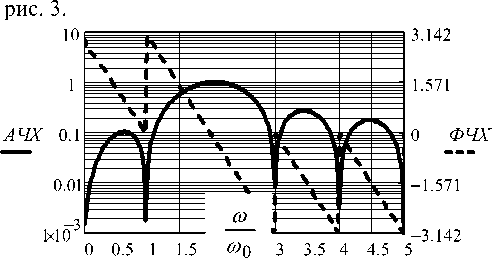
Рис. 3. Частотные характеристики фильтра второй гармоники

Для расширения полосы пропускания в алгоритме работы фильтра следует оставить обе гармонические составляющие спектра. Однако для исключения разрыва ФЧХ в полосе пропускания одну из составляющих необходимо инвертировать. Исследования показали, что полученный результат распространяется на любое количество гармонических составляющих, которые остаются в спектре после его обработки. Таким образом, синтез фильтра можно вести методом наложения. В результате получим обобщенную математическую модель цифрового фильтра для гармонического входного сигнала.

и 2

sin

1л q mAt

• m A t + co I At

P<.4 )

m

2 to -

1л q mAt

2 л cq mAt

• m A t + co I At sin to

2

2 л q co н--— mAt

2 co -

sin (cd IA t )

sin

In q mAt

1 CO A---mAt

где q – номер гармонической составляющей спектра, а р^ – определяет используемые гармонические составляющие спектра.

В качестве примера оставим в спектре выбор- ки входного сигнала одиннадцать гармонических составляющих, р^ = 10... 20. АЧХ и ФЧХ полученного фильтра показаны на рис. 4

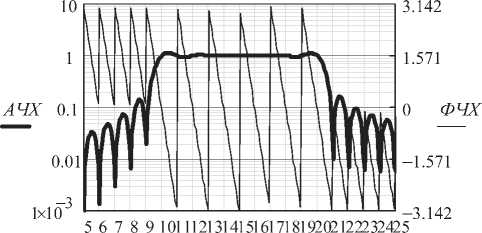
а> «о

Рис. 4. Частотные характеристики фильтра одиннадцати гармоник

Видно, что АЧХ имеет выраженную полосу пропускания, определяемую десятью отсчетами спектра входного сигнала. ФЧХ фильтра сохраняет линейность.

Численное моделирование фильтров в среде MathCAD дало 100% совпадения результатов с результатами математического моделирования.

Выводы

Исходя из полученных результатов, можно говорить о новом алгоритме синтеза неискажающих цифровых фильтров в рамках частотного метода. Высокая эффективность алгоритма достигается за счет сокращения числа математических операций по определению одного отсчета выходного сигнала. Нет необходимости определять весь спектр выборки входного сигнала. Вычисляются только отсчеты спектра, определяемые требованиями к фильтру. Обратное преобразование Фурье вырождается. При этом фильтры обладают линейными ФЧХ. Крутизна ФЧХ привязана к длительности окна. Полоса пропускания регулируется двумя способами: изменением ширины окна и изменением количества используемых отсчетов спектра выборки входного сигнала.