Алгоритм системы управления самолета при посадке на авианесущий корабль

Посадка самолета на авианесущий корабль является одним из самых ответственных и сложных для летчика этапов полета самолета. Сложность осуществления посадки самолета на корабль обусловлена необходимостью обеспечения касанием гака самолета в заданной зоне для обеспечения последующего торможения самолета аэрофинишером, выполнение посадки в условиях качки корабля до уровня 5–6 баллов и при действии на самолет возмущений воздушного потока в следе за кораблем непосредственно перед касанием палубы. На этапе посадки летчик должен обеспечить минимальные отклонения самолета по высоте от заданной глиссады и от осевой линии посадочной палубы, выдерживание заданной скорости полета для безопасного зацепления за трос аэрофинишера. Отклонение самолета по высоте от заданной глиссады летчик определяет по сигналу оптической системы посадки (ОСП), боковое отклонение – по визуальному образу положения осевой линии и линий на корме корабля, скорость полета – по сигналу отклонения от заданного угла атаки. В момент касания палубы и пробега по ней летчик испытывает значительные нормальную и продольную перегрузки. Как указано выше, в процессе посадки на корабль летчик (оператор на пилотажном стенде) осуществляет управление самолетом в продольном канале путем отклонения РУС по тангажу, отслеживая сигнал оптической системы посадки, при этом сигнал ОСП показывает угловое отклонение самолета ε от заданной глиссады:

Δh

^{£ —} L?

где Δh – отклонение по высоте от задаваемой ОСП глиссады, L – расстояние от глаз летчика до фокуса ОСП. Таким образом, посадку на авианесущий корабль можно рассматривать как задачу точного пилотирования и слежения за сигналом ε .

2.    Предложение по изменению алгоритма системы управления самолетом в продольном канале

В настоящее время принято, что на этапе посадки самолета на корабль используются те же алгоритмы системы управления, что и при посадке на обычную ВПП. В продольном канале стандартный алгоритм управления использует обратные связи по углу атаки α и угловой скорости тангажа ω _z :

У — K x вп ^X p + K a ^a + K u z вп ^w z ’

где ϕ – отклонение стабилизатора, X p – отклонение ручки управления самолета по тангажу K _{x вп} , K _α и K _{ω z} – соответствующие коэффициенты прямой и обратных связей закона управления на режиме «взлет-посадка». Данному алгоритму соответствует обычная передаточная функция вертикальной скорости для коротко-периодического движения:

V y    V K x вп M z^ϕ Y ^α

X p    p p ² + 2 ^wp + ш ² ’

где ω , ξ – частота и демпф и рование самолета с учетом обратных связей по углу атаки и угловой скорости тангажа, Y ^α – коэффициент, связанный с производной подъемной силы:

α     C y^α qS

.

У = q —-- g GV

В настоящей работе для посадки самолета на авианесущий корабль предлагается изменить закон управления (1) путем дополнения к алгоритму обратной связи по углу тангажа и изменения передаточного коэффициента от ручки управления тангажом к стабилизатору в следующем виде:

У — K x вп X p + K x к ( X p - X p ) + K a a + ( K u z вп + K u z к ) W z + K ( fl - fl * ) ’       (3)

где K _{x к} , K _{ω z к} и K _ϑ – коэффициенты алгоритма управления в режиме «корабль», символом (*) обозначены параметры системы управления, зафиксированные в момент включения режима «корабль». Аналогичный алгоритм на ряде самолетов реализован для режима «дозаправка». Алгоритму (3) соответствует структурная схема системы управления, приведенная на рис. 1. Блок «ЗУ» обозначает запоминающее устройство.

Предполагается, что включение режима «корабль» выполняется при полете самолета по глиссаде и осуществляется с помощью специального тумблера в кабине самолета. При законе управления (3) передаточная функция вертикальной скорости по отклонению рычага управления принимает вид

V y _—_________ V K x к M ^ Y ^a _________ (4)

^Xp   p[p2 + 2^*w*p + ш2] - K^MP(p + Ya) ’ где ω∗ , ξ∗ – частота и демпфирование короткопериодического движения самолета с учетом дополнительной обратной связи по угловой скорости тангажа в режиме «корабль»,

ΔX _p – отклонение ручки управления по тангажу от положения, при котором произведен переход на алгоритм посадки на корабль. Из анализа передаточной функции (4) следует, что в статике (т.е. при t ^ го или p ^ 0 ) перемещению ручки управления по тангажу соответствует приращение вертикальной скорости, в то время как при стандартном алгоритме (1) перемещению ручки управления по тангажу соответствует приращение нормальной перегрузки. В статике по закону управления (3) соотношение между перемещением ручки управления по тангажу и приращением вертикальной скорости определяется отношением передаточного числа K _{x к} к коэффициенту обратной связи по углу тангажа K _ϑ :

V y        VK x к

AX p ^{V p} ^ ⁰ K

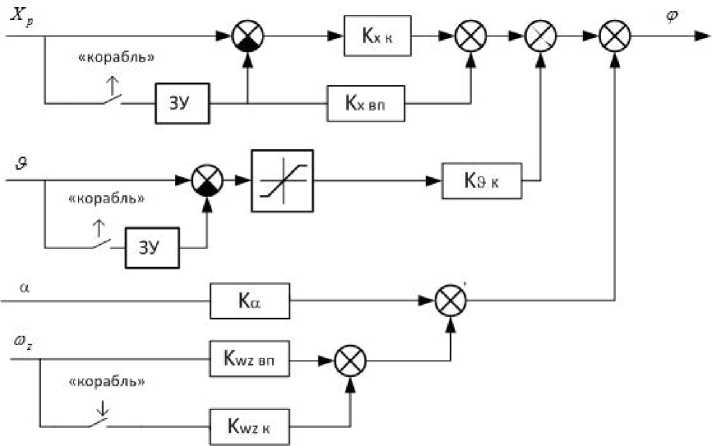
Рис. 1. Блок-схема алгоритма системы управления в продольном канале

В соответствии с этим при режиме посадки на авианесущий корабль управляемость самолета может оцениваться величиной X ^{V y} , а именно расходом ручки управления по тангажу на создание единицы вертикальной скорости:

X V y = K_.

VK x к .

Из анализа закона управления (3) следует, что при включении алгоритма на глиссаде отсутствует возмущение параметров движения самолета, при AX _p = 0 осуществляется полет с вертикальной скоростью, на которой был произведен переход на режим «корабль». Алгоритмы (1) и (3) оказываются «развязаны», что означает, что коэффициенты в алгоритме (3) могут выбираться независимо от коэффициентов закона управления (1). Для сравнения на рис. 2 приведена реакция самолета на ступенчатое отклонение ручки управления по тангажу при работе стандартного алгоритма «взлет-посадка» и предлагаемого алгоритма «посадка на корабль» при одинаковых отклонениях ручки управления по тангажу. На рисунках приведены следующие параметры: отклонение РУС по тангажу относительно балансировочного значения A X _p [мм]; вертикальная скорость V y [м/с]; нормальная перегрузка n _y ; угол тангажа ϑ [град]; угол атаки α [град].

Следует обратить внимание на то, что ступенчатому отклонению ручки по тангажу соответствует приращение вертикальной скорости, в то время как при использовании стандартного алгоритма – приращение нормальной перегрузки. При работе алгоритма посадки на корабль можно за счет выбора коэффициентов Kϑ и Kωzк добиться приемлемого качества переходного процесса, а путем выбора коэффициента Kx к – чувствительности реакции по вертикальной скорости. Предварительный выбор этих параметров был выполнен в ходе эксперимента на пилотажном стенде. В дальнейшем предполагается проведение исследований по определению приемлемых параметров переходного процесса по вертикальной скорости: времени срабатывания, заброса и чувствительности на отклонение РУС по тангажу на качество пилотирования и точность посадки на корабль.

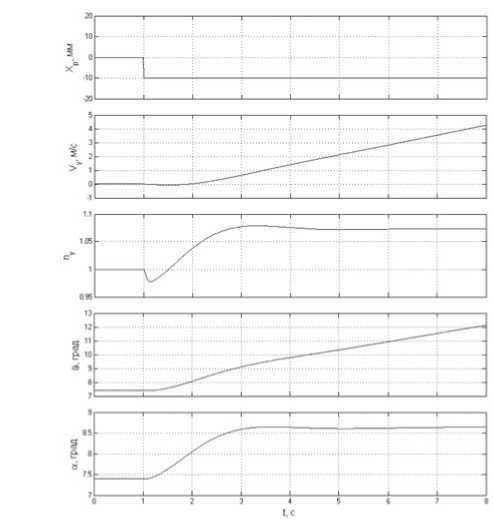
а) алгоритм «взлет-посадка»

Рис. 2. Реакция параметров движения самолета на ступенчатое отклонение РУС по тангажу

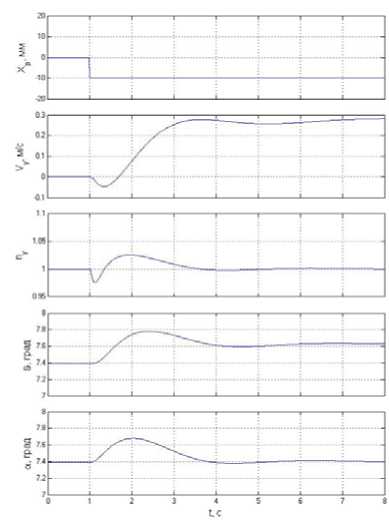
б) алгоритм «посадка на корабль»

3.    Проведение эксперимента на пилотажном стенде

Для проверки теоретических результатов и обоснования актуальности использования алгоритма «посадка на корабль» был проведен эксперимент на пилотажном стенде ЦАГИ ПС-10М. Эксперимент проводился в соответствии с методикой, ранее разработанной для обучения посадке на авианесущий корабль и оценки точности посадки в различных условиях [1–3]. Программное обеспечение для моделирования динамики полета самолета разработано с среде MATLAB/Simulink с использованием программного комплекса FlightSim для моделирования и анализа динамики самолета с системой управления [4]. В задачу оператора при моделировании посадки на корабль на пилотажном стенде входило:

• 1)    слежение за сигналом оптической системы посадки ε путем отклонения РУС по тангажу так, чтобы в процессе управления сигнал ОСП не выходил за пределы рабочей зоны ε ^m _ос ^a _п ^x вплоть до касания палубы,

• 2)    выполнение посадки при ограничениях на параметры движения самолета в точке касания гаком палубы:

• -    отклонение по дальности точки касания гаком палубы относительно расчетной точки:

iAx тк | ^ Ax mTKX ,

• -    боковое отклонение относительно оси посадочной палубы

a тк । ^ Az max ,

• -    вертикальная скорость ограничена прочностью шасси

iv y тк i <  v max .

В качестве объективной оценки качества выполняемой задачи рассматриваются гистограммы зацеплений за троса аэрофинишера, математические ожидания отклонения точки касания гаком палубы относительно расчетной точки касания и их среднеквадратичные отклонения по дальности и боковому отклонению относительно оси посадочной палубы. Степень загруженности летчика при выполнении задачи оценивается среднеквадратичным отклонением РУС по тангажу σ X _p . Субъективной оценкой летчика качества выполняемой им задачи может служить оценка PR по шкале Купера–Харпера.

Каждая серия испытаний включала в 19–20 реализаций, при этом варьировались начальное положение самолета относительно корабля и начальные условия для качки корабля. Качка задавалась в виде синусоиды с заданными частотой и амплитудой и варьируемой начальной фазой. Моделирование посадки на корабль осуществлялось при трех различных масштабах качки: 0; 0,5; 1. При этом единичному масштабу соответствует килевая качка с амплитудой 1°, боковая качка с амплитудой 3° и вертикальная качка с амплитудой 1 м. В данной серии экспериментов для исключения влияния управления скоростью моделирование посадки осуществлялось с включенным автоматом тяги.

Результаты эксперимента при рассмотренных масштабах качки приведены в виде табл. № 1–3 и гистограмм на рис. 3–5.

Для оценки продольного и бокового среднеквадратических отклонений σ x и σ z по исправленным выборочным среднеквадратическим отклонениям o x и a z вычислены соответствующие доверительные интервалы. Значение заданной надежности выбрано равным 0,99. В качестве оценки загруженности летчика вычислены усредненные среднеквадратические отклонения для сигнала от ручки управления в продольном канале о x p .

Таблица 1

Сравнение результатов статистической обработки данных для рассмотренных алгоритмов. Масштаб качкиА=0

	Алгоритм «взлет-посадка»	Алгоритм «посадка на корабль»
d x , м	10,2	6,8
a z , м	1,0	0,9
доверительный интервал для σ x ,м	4,1 <  σ x < 16,3	2,9 <  σ x < 10,7
доверительный интервал для σ z ,м	0,4 <  σ z < 1,6	0,4 <  σ z < 1,4
d X p , мм	7,0	8,7
PR	3	2

Таблица2

Сравнение результатов статистической обработки данных для рассмотренных алгоритмов. Масштаб качки А = 0,5

	Алгоритм «взлет-посадка»	Алгоритм «посадка на корабль»
d x , м	11,7	9,0
a z , м	1,3	1,5
доверительный интервал для σ x ,м	4,9 <  σ x < 18,5	3,8 <  σ x < 14,3
доверительный интервал для σ z ,м	0,6 <  σ z < 2,4	0,6 <  σ z < 2,4
d X p , мм	9,9	11,5
PR	4	3

Таблица3

Сравнение результатов статистической обработки данных для рассмотренных алгоритмов. Масштаб качкиА=1

	Алгоритм	Алгоритм «посадка
	«взлет-посадка»	на корабль»
СТ Х , м	24,5	13,2
СТ , м	1,2	1,4
доверительный интервал для σ x ,м	10,3 <  σ x < 38,7	5,5 <  σ x < 20,8
доверительный интервал для σ z ,м	0,5 <  σ z < 1,9	0,6 <  σ z < 2,3
СТ X p , мм	12,0	15,0
PR	8	5

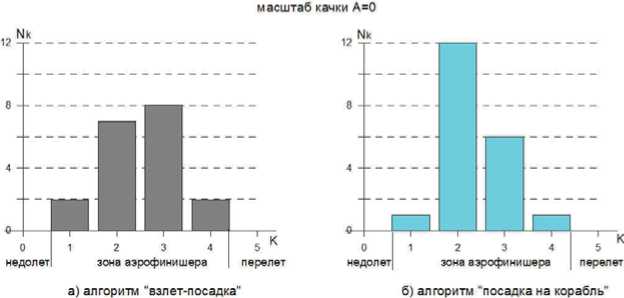
Рис. 3. Гистограммы зацеплений за троса аэрофинишера при масштабе качки А = 0

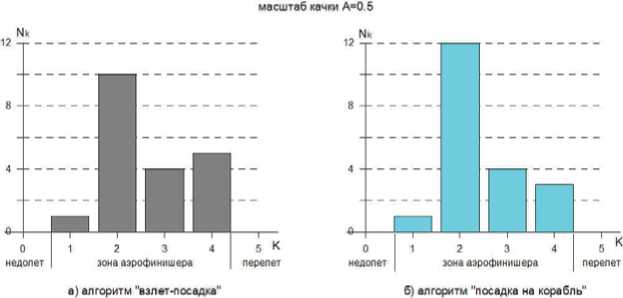
Рис. 4. Гистограммы зацеплений за троса аэрофинишера при масштабе качки А = 0,5

Гистограммы показывают распределение зацеплений гака самолета за тросы аэрофинишера в зависимости от номера троса К. Как следует из этих рисунков при масштабе качки А = 0–0,5, все посадки были выполнены с касанием гаком палубы в зоне зацепления за один из тросов аэрофинишера, при этом в 75% и более зацепления были за 2-й и 3-й троса, и полностью отсутствовали случаи недолета и перелета заданной области касания гаком палубы. При увеличении масштаба качки до А = 1 в случае исходного алгоритма системы управления «взлет-посадка» в трех случаях из 20 были отмечены касания гаком за пределами заданной области, причем два — со значительным недолетом. В процессе пилотирования по глиссаде сигнал ОСП на некоторое время ( ~ 2 с) выходил за пределы рабочей зоны, что является недопустимым, особенно вблизи кормового среза палубы.

Изменение степени загруженности оператора при выполнении посадки для исследуемых алгоритмов может быть продемонстрирована записями отклонений РУС самолета по тангажу на рис. 6. Для обоих примеров касание гаком палубы и собственно посадка самолета была достигнута в заданной требованиями зоне. Однако размах отклонений РУС по тангажу для алгоритма «взлет-посадка» вдвое превышает размах отклонений РУС для алгоритма «посадка на корабль» при одинаковых условиях моделирования. Этот же результат подтверждается оценкой среднеквадратичных оценок отклонений РУС по тангажу, проведенной на заключительном этапе посадки.

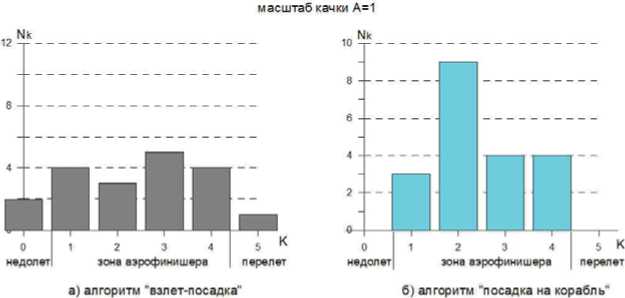
Рис. 5. Гистограммы зацеплений за троса аэрофинишера при масштабе качки А = 1

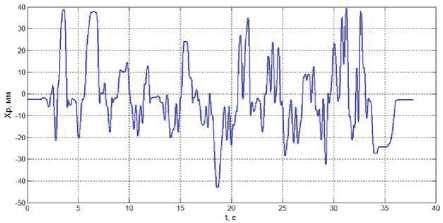
а) алгоритм «взлет-посадка»

Рис. 6. Отклонение РУС по тангажу в процессе управления самолетом при выполнении посадки в условиях качки корабля

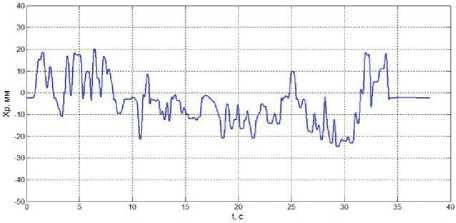
б) алгоритм «посадка на корабль»

4.    Заключение

На основании проведенного анализа и эксперимента на пилотажном стенде ПС-10М может быть сделан вывод, что предлагаемый алгоритм «посадка на корабль» позволяет обеспечить лучшую точность посадки, при выполнении необходимых условий задачи (невыхода за пределы рабочей зоны ОСП) по сравнению со стандартным алгоритмом «взлет-посадка». При этом предлагаемый алгоритм посадка на корабль имеет следующие особенности:

• - при использовании алгоритма «посадка на корабль» ступенчатому отклонению ручки управления по тангажу соответствует приращение вертикальной скорости (при использовании стандартного алгоритма «взлет-посадка» – приращение перегрузки);

• - при переключении с режима «взлет-посадка» на режим «посадка на корабль» не требуется перебалансировка ручки управления по тангажу;

• -    поскольку алгоритмы управления «взлет-посадка» и «посадка на корабль» развязаны, то выбором коэффициентов K _{x к} , K _ϑ и K _{ω z к} могут быть достигнуты требуемые характеристики управляемости и качества переходных процессов.