Алгоритм слепой идентификации MIMO-канала с циклическим сдвигом информации

В настоящее время интенсивно развиваются системы беспроводной связи (мобильный Internet, компьютерные радиосети внутри зданий и т.п.). Сильные замирания сигнала в канале затрудняют оценку переданных сообщений и приводят к искажениям передаваемой информации. Для устране- ния замираний в современных беспроводных технологиях широко применяется система MIMO,то есть система, где информация передается одновременно несколькими разнесенными передатчиками и принимается на несколько независимых приемников. Система MIMO применяется в беспроводных локальных сетях стандарта IEEE 802.11n, а также в беспроводных сетях мобильной связи WiMAX.

В настоящее время значения элементов матрицы импульсных характеристик MIMO-канала на приемной стороне определяются по тестовым им-пульсам.Однако при внесении в систему MIMO циклического сдвига передаваемой последовательности по передающим позициям в течение некоторого фиксированного интервала времени мы будем иметь избыточность, достаточную для слепого оценивания матрицы импульсной характеристики мат- ричного канала.Кроме того, в такой системе кратно увеличивается помехоустойчивость за счет разнесения каналов на приеме и передаче.

Рассмотрим MIMO-систему с N передающими и M приемными антеннами (антенными элементами). Тогда свойства MIMO-канала,соединяющего m-ый передающий элемент с n-ым приемным элементом, описываются комплексными импульсными характеристиками ^АХ Данные коэффициенты образуют матрицу импульсных характеристик н(/) размераNxM. Их значения случайно изменяются со временем из-за наличия многолучевого распространения сигнала.

В общем случае сигнал на приемной стороне записывается следующим образом:

X(/) = H(r)*S(r)+N(O, (1) где s(z) – матрица передаваемых сигналов; N(z) – матрица собственных шумов приемных элементов антенны; x(z ) – матрица принятого сообщения. Значения элементов матрицы h(z) являются основной характеристикой канала системы MIMO, а значения элементов матрицы изменяются при изменении местоположения или только приемных устройств, или только передающих, или приемных и передающих устройств одновременно. В рассматриваемой задаче канал MIMO стационарен на интервале времени передачи информационной последовательности по всем N каналам.

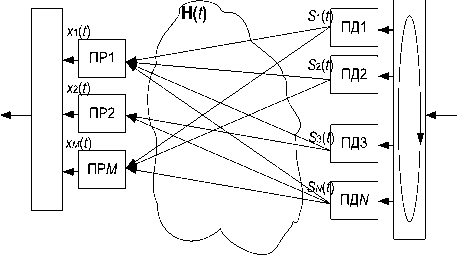
Рис. 1. Схема работы системы MIMO с циклическим сдвигом передаваемой последовательности

Для определения коэффициентов матрицы импульсных характеристик предлагается использовать метод слепой идентификации, использующий идею, описанную в [1]. В [2] был предложен алгоритм слепой идентификации одномерного векторного канала, основанный на методе взаимных отношений, имеющий эффективную вычислитель- ную структуру, основанную на аналитическом решении задачи. Найденная процедура была названа автором «алгоритмом нулевого подпространства».

В данной статье решается задача построения алгоритма слепой идентификации векторного многомерного канала связи MIMO с циклическим сдвигом информационной последовательности.

Алгоритм слепой идентификации векторного многомерного канала связи MIMO

Для решения задачи запишем уравнение, эквивалентное методу взаимных отношений, в полиномиальной форме:

L\ -1 L₂-l

EE^ti’^iXJ^)-

1 2                                                  (2)

A-i^2-i

- E E уi,h V^z\»^z^^s\ X ,/₂ (⁵2)=° -

Z^O Z2=0

где

^„/2(Z1’Z2’5)= ЕЕЕ^М/.-Л^2/1^72 5' ’ z=0 71=0 y2=0

^huS^sXTj^hih^s' ’ ^Lv^L2 - размер двумерной z=0

импульсной характеристики, M – число каналов, ^1,^2 – размер обрабатываемых фрагментов сигналов, ^o,o(⁵)>—^^-l^-lC⁵) – искомые полиномы.

Выберем 1ЦЦ - 1 различных значений формальных переменных {zi_?z₂}. Тогда мы можем записать 2L_xL₂ -1 однородных линейных уравнений относительной L_a l^ неизвестных полиномов ^,q{^s\-^ ^l_x -u₂ -i (⁵) •

В матричной форме, получим:

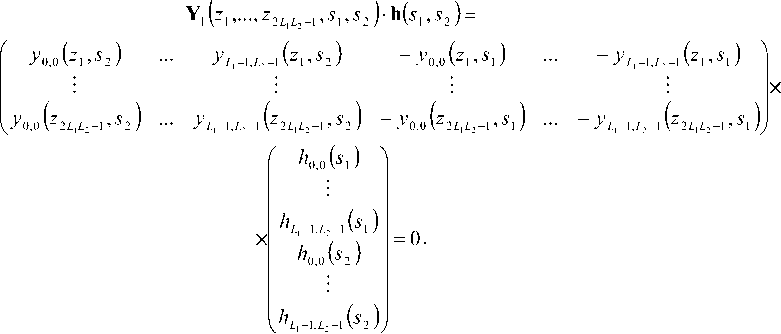
При выполнении условий теоремы о слепой идентифицируемости канала полиномиальная матрица Yj (zj ,...,Z2i   ,5[ ,5, ) имеет ранг

.

В отсутствие шума легко получить явное решение однородной системы уравнений (3). Так как хотя бы один из ее миноров порядка '2.L_XL₂ —1 MДг|,...,z₂£ ^_|,5|,5₂ J z — 1,...,2Z,,Z,₂ – номер столбца, отличен от нуля. Пусть это будет ■^2/.,/. (^Zl v, ^Z2_L1L1-_X ’ ⁵1 ’^S2 )’ тогда, полагая значение полинома ^L,-\.U-\ (⁵2 ) произвольным, получим следующую невырожденную систему

2Д£₂ -1 линейных уравнений с коэффициентами над полем С :

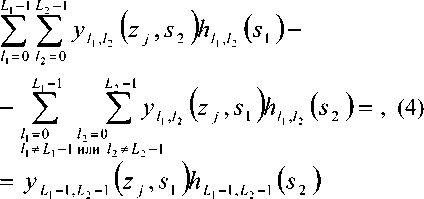
где: j — 1,...,2L_XL₂ 1. Решая ее методом Крамера, получим общее решение системы в виде:

,2L|L2 /, Z2 1

\zx,...,z2LL x,sx,s2

M, ^2£,Л V^ZX’"^-,Z2L_lL₁-\’^SY’^S2

•11

нЦ-\,Ц-\

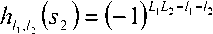
^£,£₂+Z \^ZI '■•■'^ZlL₁U-\ ’^1 ’^2

''^-Y^i-A

АЛ lx^Lx-\,

.

В силу произвольности        ) положим его равным

(—1) 1 " M2ti^ (zx ,...,z2L_x ,sx ,s2), тогда решение системы уравнений (4) с точностью до произвольного комплексного коэффициента будет иметь вид:

^1,.!, (Sl ) = (—0 M/(Z|,...,Z2t_|,5|,52),(^)

н1Х71Лй1) V 4      i’,ZlA2+/\zl’--,’z2£.|A,-l’dl>d2/’ где.

Заметим также, что нам нужно вычислить только L_xL₂ миноров, так как из анализа структуры матрицы (3) следует, что

^IL^-lVY-'-^lL^-^Sv^lb(7)

.

Таким образом, мы нашли значения неизвестных полиномов 'Ч.М-^ц-х.ь-х^ в точках         Если , этого достаточно для оценки всех коэффициентов неизвестного векторного канала:

CD _^$лД⁸^^-8хКЛ⁸^

(2) ₌ ^/7Z„/₂(⁵2)-^/7/„Z₂^l)

где l_x =0,...,L_x-\, /₂ = 0,...,Л₂-1. Для того, чтобы найти решение системы для произвольного числа каналов мы должны выполнить вычисления в кольце C[si,s₂]. Поскольку решение системы (3) по формулам (6) не содержит операции деления, то мы получим решение с точностью до некоторого полинома g(si,s₂) e C[s!,s₂].

Поскольку полиномы ^huA^s^ и ^hljA^S2) очевидно не имеют общих множителей, то неизвестный множитель ^1^2) мы можем найти как наибольший общий делитель полиномов М/ (zj Z_2Lil₂_\ , S] ,s₂) и M L^+l (²I ’•■•,2_2LiL2__x,S_x,S₂ ), используя, например алгоритм Евклида. Конечно, такой алгоритм не имеет практического значения из-за больших вычислительных затрат.

Альтернативный путь состоит в формировании системы линейных уравнений для M значений полиномов канала \Д$Л-"Л.1А^$м\

Запишем неизвестные значения в виде вектора h(sj ,...,s_M) — (Aq o^! \...,h_L __x,ц__х (»j),... ..., /z_{0 0} ^s_M ),..., h_L(__{X L2}__x (s_M )] . Тогда система линейных уравнений в матричной форме имеет вид:

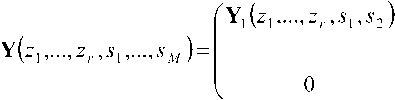
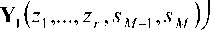
h(si„..,sA/)

= 0,(9)

где X^z_x,...,z_r,s_x,...,s_M^ (M -l)r L_XL₂M – комплексная матрица ранга ^ML_xL₂-YY r как и ранее, выбирается из условия ^M-iyr>L_xL₂ -M-Y.

Общее решение для коэффициентов канала может быть найдено далее по интерполяционной формуле Лагранжа:

м

^М=ТЛ^АМА’

Z=1

где: Z-Z(s) – элементарные лагранжевы интерполяционные многочлены, определяемые формулой:

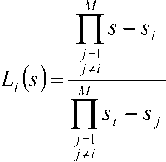
Таким образом, в отсутствие шума алгоритм слепой идентификации канала сводится к вычислению базиса нуль-пространства матрицы Y(z1,...,zr,sx,...,sMY Условия теоремы о слепой идентифицируемости векторного канала обеспечивают единственность решения этой задачи, то есть наличие единственного нулевого собствен- ного числа и соответствующего ему единственного собственного вектора с точностью до ком- плексной константы, за счет строгого равенства rank(Y(zx ,...,zr,sx M ))= MLXL2 — 1.

Данный алгоритм далее будем называть алгоритмом нулевого подпространства (АНП).

Наличие аддитивного шума в матрице входных данных ^zx,...,zr,sx,...,sM^ = Y(z1,...,z,.,s1,...,sM)+V(z1,...,z,.,s1,...,sAJ создает условия, когда rank^zx,...,zr,sx,...,sM^ может быть равен ML или может быть меньше ^lm-yY В первом случае нуль-пространство матрицы состоит только из нулевого вектора,а во втором содержит несколько базисных векторов. Поэтому задача слепой идентификации может вообще не иметь решения или решение задачи становится неоднозначным.

Как уже отмечалось выше, в этом случае мы можем использовать стратегию метода наименьших квадратов, то есть в качестве решения задачи для случая rank^¥^z_x ,...,z,.,s_{x M} ))= ML_XL₁ взять собственный вектор, соответствующий минимальному по модулю собственному числу матрицы Y* (zi,„ .,z_r, Si ,...,s_a/)y(zi ,...,z_r, 51,. ..,s_MY.

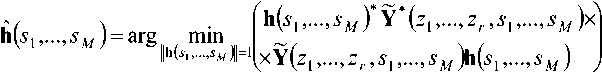
В этом случае решение задачи всегда единственно и, как известно, минимизирует функционал ^„....г,.,^,..^!,)^,,...^!,^ при ограничении нормы |h(si,...,sMf =1 .

Поскольку выбор числауравненийи,соответс-твенно,числастроквматрице xY:_x,...,z_r,s_x,...,s_NA в нашей интерпретации произволен, то мы можем выбрать их число строго равным (l_xl₂m-yY Тогда rank^y^z_x,...,z_r,,s_x,...,s_M^< ML_XL^ -1 теперь уже за счет линейной независимости строк. При этом, поскольку r = ^L_XL,M -YY^M -Y^ целое только в частных случаях, то мы выбираем r как наименьшее целое, а r так, что (M -1)- r + r ^ L_XL₂M - Y. При этом

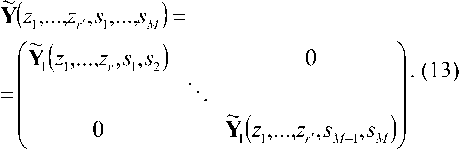
Теперь мы можем решать задачу слепой идентификации векторного канала при наличии шума, используя алгоритмы точного решения однородной системы уравнений.

При этом, поскольку нуль-пространс-тва матрицы Nkzv-,z_r.,s_x,...,s_M^ и матрицы Y^Z!,...,^!,...^^,...^^ совпадают, то решение, получаемое, например, по формулам (6), и решение вариационной задачи (12) совпадают с точностью до комплексного множителя, и являются нормальным псевдорешением однородной системы уравнений (9). Таким образом, мы показали эквивалентность оценки АНП и оценки, полученной в рамках метода наименьших квадратов.

Несмотря на то что формулы (10) дают явное решение, непосредственное их использование для нахождения численного решения однородной системы, задаваемой матрицей (13), нецелесообразно даже при сравнительно небольших размерах матрицы, поскольку требует вычисления ^L.M-Y^ определителей размера (lxl2m-yY Поэтому более целесообразно использование ал- горитмов, имеющих меньшие вычислительные затраты.

Одним из таких методов может быть несколько модифицированный метод Перселла. В рамках данного подхода мы интерпретируем систему однородных уравнений с матрицей (13) как условия ортогональности вектора h(si,...,s_A/) с (£1^-1) линейно независимыми строками матрицы (13). При этом решение системы находится путем построения базисов подпространств унитарного линейного пространства ^~r L_XL-)M убывающих размерностей:

= R0 d^.-d^ ^...^R^^,

где R^ – подпространство, состоящее из векторов, ортогональных к первым к строкам У1,-Лк матрицы y(z₁,...,z,,,s₁,...,s_a/).

Базис подпространства ^k строится из базиса подпространства R^ в виде следующих линейных комбинаций:

.

I              I                  I rv                                                           1 Д

Коэффициенты c'j определяются из ус- ловия ортогональности строк матрицы

N^_V...,Z,,,S_X,...,S_M^ и вектора решения в виде

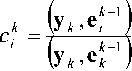
Для реализуемости процесса необходимо, чтобы скалярные произведения (y^ei?¹) были отличными от нуля. Если к — 0 , то в качестве базиса берется естественный базис в ^~r L_x M , e?=(l,0,...,0),...,e«_ii2M=(0,...,0,l).

Подпространство ^L.L,M-\ является нуль-про-странством матрицы Y(zx,...,zr,,sx,..„sMV так как единственный базисный вектор этого подпро- странства ортогонален ко всем линейно независимым векторам У I’--, У l,l2m-v и является численным решением системы однородных уравнений, заданных матрицей (13).

Таким образом. мы получили итерационную модификацию АНП, которая, конечно, с точки зрения погрешности, эквивалентна АНП в аналитической форме, но требует меньших вычислительных затрат.

Выводы

Получен алгоритм слепой идентификации MIMO-канала с циклическим сдвигом передаваемой последовательности. Получена эффективная с вычислительной точки зрения модификация данного алгоритма, т.е. последовательность вычислений, содержащая минимальное количество операций сложения и умножения, имеющая простую структуру вычислений.