Алгоритм совместного оценивания функционально связанных координат и состояния групповой воздушной цели на основе линейной модели с марковской структурой

Анализ современных вооруженных конфликтов отмечает групповой характер применения авиации. При этом значительный вклад в эффективность истребителя при решении задач перехвата и уничтожения групповых воздушных целей (ГВЦ) вносят функциональные возможности и точностные характеристики его бортовой радиолокационной станции (БРЛС) по обнаружению, разрешению, сопровождению и распознаванию воздушных целей (ВЦ) различных типов и классов.

Под ГВЦ в рамках решаемой задачи понимается определенным образом функционально связанное в пространстве расположение средств воздушного нападения (самолетов, ракет, вертолетов, беспилотных летательных аппаратов), находящихся в главном луче диаграммы направленности антенны БРЛС истребителя и действующих по единому тактическому замыслу.

В работах [1–4] предлагается расширение информационных возможностей БРЛС за счет реализации на борту истребителя новых алгоритмов распознавания таких состояний ГВЦ, как ее численного и типового (классового) составов, функционального назначения самолетов в группе по принципу «ведущий – ведомый», формы боевого порядка (БП) (пеленг, клин и т. д.), характера ее полета по принципу «стационарный полет – маневр группой – маневр в группе», видов оказываемого информационного противодействия (уводящие по скорости и/или по дальности помехи), а также фактов и количества пущенных ракет.

Основу этих алгоритмов составляет многогипотезная многомерная линейная калманов-ская фильтрация [3], строящаяся на априорных сведениях в виде динамических моделей (ДМ) функционально связанных координат (ФСК) по двухэтапной схеме «прогноз – коррекция». При этом под ФСК понимают дальности до элементов ГВЦ, радиальные скорости и ускорения взаимного сближения самолетов группы и истребителя – носителя БРЛС, а также дистанции между самолетами в БП.

Однако примененная в вышеупомянутом подходе калмановская фильтрация имеет ряд ограничений:

не позволяет учитывать априорные сведения о динамике распознаваемых состояний ГВЦ, а как следствие, и возможность влияния ФСК на состояние ГВЦ;

не позволяет учитывать дополнительную статистическую взаимосвязь между ФСК и состоянием ГВЦ;

линейность моделей полета ГВЦ и БРЛС как системы наблюдения, положенных в основу синтезированных алгоритмов;

при решении задачи фильтрации не рассмотрены такие реальные динамические свойства измерителей, как инерционность, форсирование и запаздывание;

не рассматривается возможность комплексирования информации от индикаторов состояния ГВЦ;

не рассматривается возможность комплексирования информации от измерителей ФСК и индикаторов состояния ГВЦ (теплопеленгаторов, индикаторов помех, огневого противодействия и т. д.), отличных по физическим принципам от радиолокационных;

не позволяет учитывать влияние управления истребителем и его состоянием на ФСК и состояние ГВЦ.

В свою очередь, на практике имеет место:

возможность выявления и описания закономерностей смен различных состояний ГВЦ во времени;

зависимость численного состава ГВЦ, функционального назначения самолетов группы, формы ее боевого порядка, характера полета, вида помех, фактов пуска ракет, их количества и направления полета от радиальных дальностей, скоростей и ускорений;

ограничение допустимых диапазонов скоростей и ускорений летательных аппаратов, образующих ГВЦ, летно-техническими характеристиками их типов или классов;

ограничение возможных видов огневого и информационного противодействия, а также функционального назначения самолетов в группе их типами и классами;

наличие и возможность учета значительных нелинейностей в динамике фазовых координатах полета ГВЦ, в частности состоящих из сверхманевренных летательных аппаратов, и в БРЛС при измерении ФСК в условиях интенсивного информационного противодействия;

проявление в реальных измерителях инерционности, форсирования и запаздывания;

возможность комплексирования измерений ФСК, получаемых от БРЛС, с показаниями индикаторов (например, информационного или огневого противодействия).

Отсутствие возможности учета этих особенностей при калмановской фильтрации в целом отрицательно сказывается на адекватности используемых при оценивании и распознавании моделей, а как следствие, снижает функциональные возможности и точностные характеристики БРЛС по сопровождению и распознаванию ВЦ различных типов и классов.

Возможным путем устранения отмеченных ограничений признано моделирование полета ГВЦ и смены ее состояний как системы со случайной скачкообразной структурой (ССС) и применение в «многогипотезном» подходе вместо фильтра Калмана рекуррентных алгоритмов [5], по отношению к которым линейная калмановская фильтрация является частным случаем.

Цель статьи - разработать алгоритм совместной фильтрации радиальных функционально связанных координат самолетов звена и распознавания формы их боевого порядка и варианта выдерживаемых дистанций в интересах расширения функциональных возможностей и повышения точностных характеристик бортовой радиолокационной станции истребителя по сопровождению и распознаванию групповых воздушных целей.

Для этого необходимо решить следующие частные задачи:

формализовать систему «ГВЦ – истребитель» как систему со ССС;

усовершенствовать ДМ полета звена самолетов как линейную систему с марковской структурой для случая смены форм БП и дистанций в них;

синтезировать квазиоптимальный алгоритм совместной фильтрации ФСК и распознавания состояния ГВЦ на основе линейной модели с марковской структурой и метода двухмоментной параметрической аппроксимации.

Групповая воздушная цель как система со случайной скачкообразной структурой

Под системой со ССС понимаются стохастические динамические системы, структура которых (т.е. состав элементов и связи между ними) имеют конечное число возможных состояний, сменяющих друг друга в случайные моменты времени [5].

Так, группу воздушных целей при решении задачи их совместного сопровождения-распознавания в БРЛС истребителя можно представить системой со ССС, в которой ФСК соответствуют фазовым координатам, а состояния ГВЦ – состояниям структуры системы.

Тогда под случайной скачкообразной сменой структуры понимается изменение численного состава ГВЦ (рис. 1) в результате отделения от нее самолетов или их поражения, смена форм боевого порядка (рис. 2), переход от стационарного полета к выполнению маневра в группе или составом группы, начало постановки помех, смена их вида (по скорости, по дальности) (рис. 3), изменение количества пущенных ракет (рис. 4), а также смена направления их полета по принципу «на меня» - «не на меня» (рис. 5), происходящие в случайные, заранее не известные моменты времени.

Функциональная схема совместного траекторного сопровождения-распознавания ГВЦ на основе модели со ССС представлена на рис. 6.

На вход обобщенного объекта управления, под которым понимается ГВЦ и противоборствующий ей истребитель - носитель БРЛС, кроме управляющих сигналов u k , 9 k поступают неуправляемые случайные возмущения 4 k .

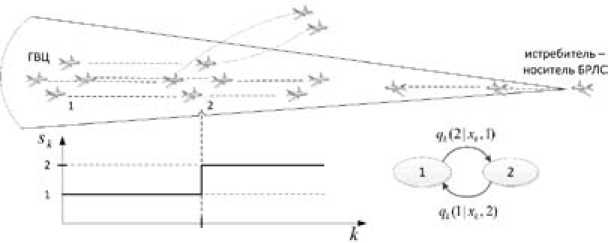
Рис. 1. Скачкообразное изменение численного состава ГВЦ: 1 – звено; 2 – пара; внизу, справа – граф состояний ГВЦ

Fig. 1. Spasmodic change of numerical structure of clustered air target: 1 – link; 2 – pair; below, on the right – state graph of group air target

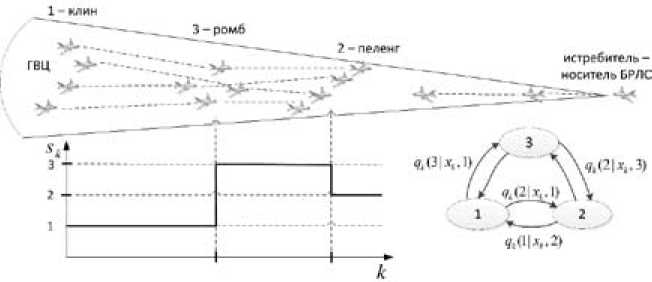
Рис. 2. Смена формы боевого порядка ГВЦ: 1 – клин; 2 – пеленг; 3 – ромб

Fig. 2. Spasmodic change of a form of a fighting order of clustered air target: 1 – wedge; 2 – bearing; 3 – rhombus

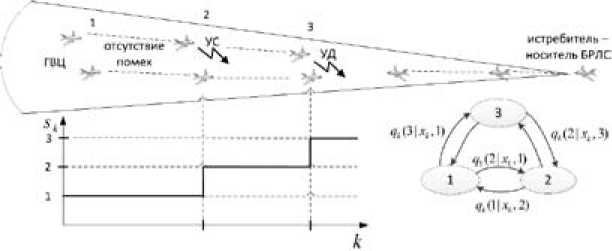
Рис. 3. Смена вида информационного противодействия со стороны ГВЦ: 1 – помехи отсутствуют; 2 – ставится уводящая по скорости помеха; 3 – ставится уводящая по дальности помеха

Fig. 3. Spasmodic change of information counteraction from clustered air target: 1 – there are no interferences; 2 – a distraction that distracts by speed is set; 3 – an disturbship distractor is placed

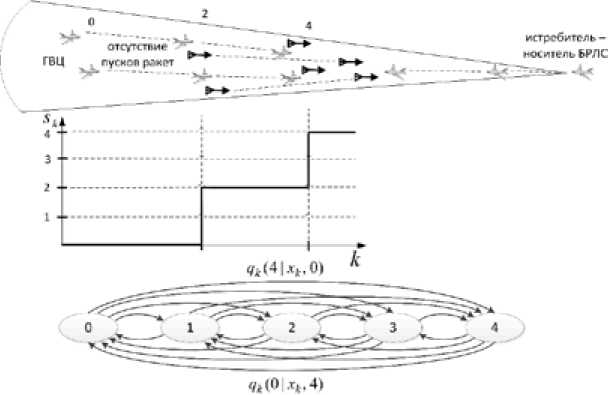
Рис. 4. Скачкообразное изменение количества пущенных ракет

Fig. 4. Spasmodic change of quantity of the started-up rockets

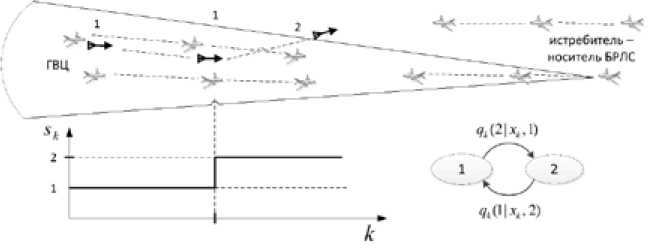
Рис. 5. Скачкообразное изменение направления полета ракеты: 1 – «на меня»; 2 – «не на меня»

Fig. 5. Spasmodic change of the direction of flight of a rocket by the principle: 1 – “on me”; 2 – “not on me”

Состояние объекта «ГВЦ – истребитель» в дискретный момент времени характеризуется векторами x k и s k . Состояние x k, s k наблюдается с помощью БРЛС, измеряющей ФСК, с вектором выходных сигналов z k и с помощью индикаторов состояния ГВЦ с вектором выходных сигналов r k . Информация о состоянии «ГВЦ ^- истребитель», содержащаяся в сигналах z k , r k , является неполной и искаженной помехами U

Оценивание текущего (мгновенного) состояния ГВЦ и истребителя как системы со ССС – это распознавание состояния их структуры s k и оценивание ФСК x k на основании наблюдений zk _и rk ■

Оценки экстраполяции ~_к ,s_k , фильтрации x _k , s _k и интерполяции x _k , ( _k могут использоваться для выработки сигналов управления u k , ⁹ ■

В задаче синтеза системы обработки информации предполагаются известными модели системы «ГВЦ – истребитель», системы наблюдения и управления, а алгоритм совместного траекторного сопровождения-распознавания подлежит определению. Так как зависимости u_k,

Неулред-ееише вождей ста ил

с

а ^

Обобщенный объект управления; ГВЦ - истребитель: система со ССС

□ s’

Состояния ГВЦ

Объект наблюдения ГВЦ свямннне коорди*<вты:

- дальность;

«скорость;

- ускорение

ЧС|фН| Форма БП |хп | ТС | КС |гк> ...

фазовые координаты относительного и абсолютного движения ЛА и ГВЦ

Сбъеитуправления-истребители

Смеянне прптгры «стрейтло.

Колм*, вето г'уии’имгих р»»»т|ауд •*»►•*«>» Рс*рм работы двигJTCZ* Е.«д помете мшитм ВИД целгра: трртит™, .ня Решим рАоы ЕГЛС

I Метод |«г»едения .

112. S,p S^

ф-

Ичци^ир ♦—

Распом*»вс

СоСтолнгч ГВЦ

S травление

СТРУКТУРОЙ

и x,R;x,R;x,R;

система

.и^игл.пичиски<и управления

Х(5Л)

Х^.^)

УЛрнипчие »тн«даинальнп

■‘w....... кирдянэтащ

С.н-шюнал I ■“”■”"* координат

Алгоритмическое обссгэтченнг

система информационно-

вычислительная система

Радиоэлектронная система управления истребителя

Рис. 6. Функциональная схема совместного траекторного сопровождения-распознавания ГВЦ на основе модели со ССС: ЧС – численный состав; ФН – функциональное назначение; БП – боевой порядок; ХП – характер полета; ТС – типовой состав; КС – классовый состав; ПО – помеховая обстановка; РП – ракетное противодействие

Fig. 6. Function chart of joint trajectory maintenances recognitions of clustered air target on the basis of random jump structure model: ES – the number of people; FN – functional purpose; BP – battle order; HP – the nature of the flight; TC – typical composition; KS – class composition; ON – jamming environment; RP – rocket counteraction

θk от оценок ФСК и состояния ГВЦ предполагают детерминированными и известными, а сами оценки ищут в классе детерминированных зависимостей от наблюдений zk и rk, то математиче- ские модели можно записать в следующем виде: для ФСК xk+1 = Фк(sk+1,xk,sk,^k), k =0,1,2,-,                                          (1)

для измерений БРЛС zk+1 = Vk(xk+1, sk+1, rk+1, xk, sk, zk, zk),                                              (2)

где k – дискретный момент времени; x_k – вектор ФСК; s_k – вектор состояний ГВЦ; z_k – вектор измерений ФСК; r k – вектор индикации состояния ГВЦ; ξ k – вектор возмущений, действующих на объект (дискретный белый шум); ζ_k – вектор помех измерению.

Размерность векторов равна соответственно n x , n s , n z , n r , n_t, n_c .

Возмущения $ k и помехи Z k — последовательности векторных случайных величин, независимых при разных к .

Индекс s_k состояния ГВЦ и выходной сигнал индикатора r_k – условно марковские цепи с конечным числом состояний, заданные условными вероятностями переходов (графы состояний представлены на рис. 1–5):

q k ⁽ s k ,1k * . . s k ).                                                                        (3)

П + 1 ( r . + i | x . + 1 , s i + 1 , X k , s . ,Z k , r k ).                                                     (4)

Таким образом, влияние u_k, 9_к в (1), (2) учтено с помощью функций ф_к (•), ^_к (•), а влияние возмущений и помех в (3), (4) - с помощью функций q_k (•) и п_{к +1}(-) в неявной форме.

Для индикатора состояния структуры характерно принятие решения по результатам наблюдения без учета априорной информации (3) о динамике состояний ГВЦ.

Известны также:

φ_k (∙) и ψ_k (∙) – векторные детерменированные функции случайных аргументов; совместная функция распределения возмущений и помех

Ф _k ( Z _k , £ _k );                                                                    (5)

начальное совместное распределение вероятностей ФСК и состояния ГВЦ f0( x 0, s 0).                                                                                     (6)

Зависимость q_k (•) от х_к отражает тот факт, что изменения состояния ГВЦ не только происходят под влиянием внешних воздействий, но и зависят от ФСК, что в общем случае отражает «переход количества в качество».

Как следует из (1)–(4) временная последовательность векторов мгновенного (текущего) обобщенного состояния ГВЦ и системы наблюдения

^[ x k , s k , z k , r k ]

является марковским процессом.

Теоретическая особенность представления ГВЦ как системы со ССС в отличие от случая калмановского фильтра при «многогипотезном» подходе состоит в следующем [5].

Несмотря на то что вектор состояния [ х_к, $_к ] марковский, поскольку ф_к (•) и ^_к (•) не зависят от вектора наблюдений [ 2 к , Г к ], его составляющие в отдельности (вектора ФСК Х к и состояний ГВЦ ^s ) марковским свойством не обладают. Они являются условно марковскими: при фиксирован ном состоянии Г ВЦ $_к = i ; вектор х_к(i ) - марковский процесс, а при фиксированном х_к = j индекс состояния ГВЦ $_к(j' ) - марковская цепь.

В свою очередь, вектор наблюдения [2к, гк], как целиком, так и каждая его компонента в отдельности, представляют собой условные марковские процессы. Однако вектор состоя-– 48 – ния обобщенной системы «ГВЦ - индикатор - БРЛС» [xk, sk, zk, rk] является марковским, что обуславливает рекуррентную форму алгоритмов, удобную для реализации в БЦВМ истребителя.

Таким образом, разработана в общем виде математическая модель (1)-(6) ГВЦ как системы со ССС, позволяющая:

учитывать априорные сведения о динамике распознаваемых состояний ГВЦ в виде условных вероятностей переходов (3);

учитывать дополнительную статистическую взаимосвязь между ФСК и состоянием ГВЦ: в выражение (1) ФСК x k ₊₁ зависят от состояний ГВЦ s k ₊₁ и s k , а в выражение (3) вероятности перехода q k (∙) зависят от ФСК x k ;

описывать в (1) и (2) заданием конкретного вида соответственно функций ф_к (•) и y k (•) нелинейные модели динамики ФСК и измерений БРЛС;

отражать в (2), (4) такие реальные динамические свойства измерителей и индикаторов, как инерционность, форсирование и запаздывание;

рассматривать дополнительную информацию, поступающую от индикатора со статистической характеристикой (4) (вероятностью правильной/ложной идентификации);

представлять в (2), (4) информацию, поступающую от измерителей ФСК и индикаторов состояния ГВЦ, отличных по физическим принципам от радиолокационных, с целью ее последующего комплексирования с информацией, выдаваемой БРЛС.

Определение конкретных видов зависимостей (1)-(6) позволяет получить на основе известных результатов теории систем со ССС 151 новые оптимальные и квазиоптимальные рекуррентные алгоритмы для решения задачи совместного сопровождения и распознавания ГВЦ в БРЛС истребителя, отличающиеся повышенной точностью.

Однако для этого необходимо усовершенствовать динамические модели, разработанные для калмановской фильтрации.

Динамическая модель стационарного полета звена

В работе [6] приведена ДМ стационарного полета пары самолетов, описываемая следую- щей системой уравнений: = V0 + w t ;(7)

Vi(t) = AVi(t) = ai(t),   AV,(0) = AVo,;(8)

ai(t) = -aiai(t)-P^(t) + (2^)^(t), ai(0) = a0l,(9)

d (t) = AV (t) - AV (t) d (0) = d(10)

V2(t) = V + AV2(t);(11)

^(t) = a2(t) = -a2a2(t)-p2AV2(t) + y d3(t), a2(0) = a02, гдеV1(t), V0 и AVj(t) - скорость стационарного полета ведущего (ВЩ) самолета, ее постоянная и флюктуационная составляющие соответственно;

A V_0i - начальное значение флюктуационной составляющей скорости ВЩ;

а1(t) и а01 - флюктуационная составляющая ускорения ВЩ и ее начальное значение соответственно;

а1, в^ о2а1 — параметры модели ВЩ, вычисляемые по формулам ai = 1/Ti; в1 = (2п fi)2; g2.; = o2. (a2i + pi);                                           (14)

т_ь f и o _vi - соответственно время корреляции, частота и среднеквадратическое отклонение скоростных флюктуаций полета ВЩ;

n(t) - формирующий белый гауссовский шум (БГШ) с нулевым математическим ожиданием и единичной интенсивностью (спектральной плотностью);

dз(t) - текущее значение выдерживаемой ведомым (ВМ) самолетом дистанции относительно ВЩ;

d _i i , ₂ - заданная дистанция, выдерживаемая ВМ самолетом относительно ВЩ;

• V₂(t) и A V 2 - скорость стационарного полета ВМ и ее флюктуационная составляющая соответственно;

• A V 02 - начальное значение флюктуационной составляющей полета ВМ;

• а₂(t) и а₀₂ - флюктуационная составляющая ускорения ВМ и ее начальное значение соответственно;

• a ₂, Y - параметры ДМ полета ВМ, вычисляемые по формулам

a 2 = X ( o vi + Ao ) / d з (t); у = в 2 a 2 / K;                                          (15)

• в ₂, Ao и K - параметры ДМ полета ведомого самолета, зависящие от заданной для выдерживания ВМ дистанции d_i,2;

• в ₂ - квадрат частоты скоростных флюктуаций ВМ;

Ao - приращение среднеквадратического отклонения скоростных флюктуаций ВМ относительно среднеквадратического отклонения скоростных флюктуаций o vi ВЩ;

K - коэффициент устойчивости управления ВМ при выдерживании им заданной дистанции.

Под стационарностью полета звена в настоящей работе понимается постоянство детерминированной составляющей V0 радиальных скоростей взаимного сближения самолетов группы с истребителем – носителем БРЛС.

Структура описанной ДМ представлена на рис. 7.

Недостатком данной ДМ стационарного полета пары самолетов является отсутствие возможности с ее помощью адекватно описать стационарный полет звена из четырех самолетов с учетом динамики смены форм БП и задаваемых для выдерживания дистанций между самолетами группы.

Данная неадекватность негативно влияет на качество разрабатываемых алгоритмов сопровождения ВЦ и распознавания функционального назначения самолетов группы по принципу «ведущий – ведомый» и формы их БП, а также на качество моделирования таких алгоритмов с целью получения их характеристик.

При этом выражения (7)–(15) недостаточны для применения аппарата теории систем со ССС.

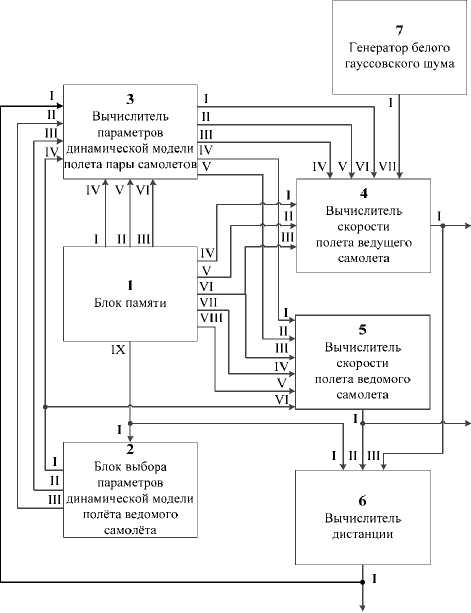
Рис. 7. Структура модели стационарного полета пары самолетов

Fig. 7. Structure of model of stationary flight of couple of planes

Динамическая модель полета звена со сменой форм боевых порядков и дистанций в них

С целью устранения отмеченной неадекватности ДМ стационарного полета пары самолетов обобщена на случай полета звена из четырех самолетов, а также в ней учтена возможность смены форм БП и выдерживаемых дистанций между самолетами группы.

Предлагаемая модель строится при следующих допущениях:

• -    время полета ГВЦ в одной форме БП значительно превосходит время ее перестроения в другую форму БП;

• -    время полета звена при выдерживании его самолетами одного варианта заданных дистанций значительно превосходит время набора этими самолетами нового варианта дистанций.

Сделанные допущения позволяют моделировать смены форм БП и вариантов выдерживаемых дистанций между самолетами группы случайными скачкообразными процессами.

Усовершенствованная ДМ стационарного полета звена самолетов описывается следующими выражениями:

для ФСК (фазовых координат) системой уравнений

V 1 ^{( t} ) = V 0 + AV ,( t ) ;                                                        (16)

V1(t) = AV1(t) = a1(t), AV1(0) = AV01; ai(t)-^C)-e^Vl(t)+(2-? ^^(t >-i(0)-"el» (17) (18) d mi,i (t ) = AVmi (t)-AVi (t), dmi-i (0) = ^^ (19) V (t)_ V +.V (t ). i0i (20) Vi(t )=AVi (• )=ai(. 1 AV(0) = AV„i; (21) .                                                                                                         X ai          αijai         ij i       γij mi,i , аi        а0i; i = 2,3,4; m, = 1.2.3, m-(m2.m3.m4), j-ij; (22) (23) для смены форм БП звена и вариантов выдерживаемых дистанций (структуры звена)

t_k., = t_k + min T   : j * h_k} , n = arg min , T ~ Exp{ ^ } ;

lx + 1        lx                ' 11 k , j v          lx " ^{J iX} k + 1      *'*’^X g            V * h j ) ^ ij             A ij ' '

j * hk k’ xn+1 = xn + min{nr j : j * rn}, rn+1 = argmin{nr J, Пц ~ Exp{ ^} ; n                                     j *r„         n

'ho,to < t < ti; [ro,xo < t < X1; h1,t1 < t < t2; Г1,Х1 < t < X2; s1(t) = ^ K                    S2(t) = ^ K                        (24) hk,tk < t < tk+1; rn,xn < t < tn+1; Ik K где наряду с ранее введенными обозначениями,

• V i (t) – радиальная скорость i-го самолета звена относительно БРЛС (i = 1 соответствует ВЩ);

;

ΔV i (t) – флюктуационная составляющая радиальной скорости i-го самолета звена;

ai(t) – радиальное ускорение i-го самолета звена относительно носителя БРЛС;

dm i(t) – текущее значение дистанции между i-м и mi-м самолетами; i, dj,mi,i(t) – заданная для выдерживания дистанция между i-м и mi-м самолетами, соответствующая j-му варианту заданных дистанций;

α_i j ,β_i j ,γ_i j , – коэффициенты для i-го самолета звена при j-м варианте заданных дистанций;

a y = K ij ( o vi + Ao ij ) / d jm i ; _Y y = p у a у / K y ;                          (25)

ΔV ₀₁ , a ₀₁ ,d jm i ,i ,ΔV 0i , а _0i , – начальные значения соответственно флюктуационной составляющей скорости ВЩ, ускорения ВЩ, заданной дистанции между i-м и m_i-м самолетами, соответствующей j-му варианту заданных дистанций, флюктуационной составляющей скорости i-го ВМ самолета, ускорения i-го ВМ самолета;

i – условный порядковый номер ЛА в звене (i = 1 соответствует ВЩ);

m_i – условный порядковый номер ЛА, относительно которого выдерживает заданную d j,m _i ,i (t) дистанцию i-й самолет звена;

m = (m2, m3, m4) – вектор, задающий форму БП (например, для БП «пеленг» m = (1,2,3), а для – «клин» m = (1,1,3));

tk – случайные моменты смены формы БП звена;

h k – номер индекса формы БП (1 – пеленг, 2 – клин), в который звено перестраивается в момент t_k;

X ~ p i (0) – начальное значение формы БП, заданное рядом распределения p i (0);

τ_ij ~ Exp{ λ_ij } – случайные интервалы времени между сменами форм БП звена, распределенные по экспоненциальному закону с параметрами λ ij ( λ ij – интенсивность перестроения звена из i -й формы БП в j -ю);

s 1 (t) – марковский случайный скачкообразный (импульсный) процесс смены форм БП;

xk – случайные моменты смены задаваемых для выдерживания дистанций при hk-й форме БП звена;

rk – номер варианта задаваемых для выдерживания дистанций при hk-й форме БП звена, на который в момент x меняется текущий вариант;

Y ~ q_i (0) – начальное значение варианта задаваемых для выдерживания дистанций, заданное рядом распределения q i (0);

η_ij ~ Exp{ μ_ij } – случайные интервалы времени между сменами вариантов задаваемых для выдерживания дистанций, распределенные по экспоненциальному закону с параметрами μ ij ( μ_ij – интенсивность замены i -го варианта задаваемых дистанций на j -й);

s 2 (t) – марковский случайный скачкообразный (импульсный) процесс смены вариантов выдерживаемых дистанций.

Коэффициенты α 1 , α ij и величина σ ₁ характеризуют соответственно ширину спектра и дисперсию ускорения ведущего самолета.

Коэффициенты β , ограничивающие рост дисперсий скоростей во времени, зависят от типа объекта и условий движения.

Структурная схема разработанной ДМ представлена на рис. 8. Так, в структуру известной модели добавлены два вычислителя скорости ведомых самолетов, два вычислителя дистанций, вычислитель формы БП звена, вычислитель варианта выдерживаемых дистанций и переключатель структуры модели. Помимо этого, в блок памяти добавились распределение p i (0) начальной формы БП звена, распределение q i (0) начальных вариантов, задаваемых для выдерживания дистанций, интенсивности λ_ij и μ_ij соответственно перестроения звена в различные формы БП и смены вариантов дистанций, начальные значения скоростных флюктуаций ∆ V 03 и флюктуаций ускорения а₀₃ третьего самолета, начальные значения скоростных флюктуаций ∆ V 04 и флюктуаций ускорения а 04 четвертого самолета; блок выбора параметров ДМ расширился для хранения параметров полета ведомых самолетов β ₂ j , β ₃ j , β ₄ j , ∆σ _i j и K_i j , для различных вариантов j , заданных для выдерживания БП дистанций d j m _i ,2 , d j m _i ,3 , d j m _i ,4 ; вычислитель параметров ДМ дополнительно стал рассчитывать α ₄ j , γ ₄ j , α ₃ j , γ ₃ j , α ₂ j , γ ₂ j , также зависящие от вариантов j , заданных для выдерживания БП дистанций.

Для проверки функционирования разработанной ДМ рассмотрен частный случай смен форм БП «пеленг» и «клин» и трех вариантов задаваемых дистанций.

При этом система дифференциальных уравнений (17)–(19) и (21), (22), описывающих полет звена в векторно-матричной форме, примет следующий вид:

d^X(t) = A(s)X(t) + G'N(t) , X( 0 ) = X _o,                            (26)

dt где X(t) = (AV1,a 1,d 12,AV2,a2,dm (s)3,AV3,a4,d34,AV4,a4)T - вектор фазовых координат звена;

N ( t ) = ( n 1 ,n 2 ,n 3 ,n 4 ,n 5 ,n 6 ,n 7 ,n 8 ,n 9 ,n 10 , n 11 ) T — матрица формирующих БГШ с нулевыми средними значениями и единичными интенсивностями;

A ( 5 ) - матрица коэффициентов, зависящих от формы БП и задаваемых дистанций;

G' - матрица коэффициентов размерности 11x11, имеющая следующий ненулевой элемент:

g 2 ₂ = V 2aiO2 ;                                                        (27)

• X ) - начальное значение вектора фазовых координат.

Отличительной теоретической особенностью матричного уравнения (26) от представленного в [3] является зависимость коэффициентов матрицы A ( 5 ) от состояния 5 структуры звена самолетов (рис. 9), что обуславливает наличие не одной матрицы, а такое их количество, кото-

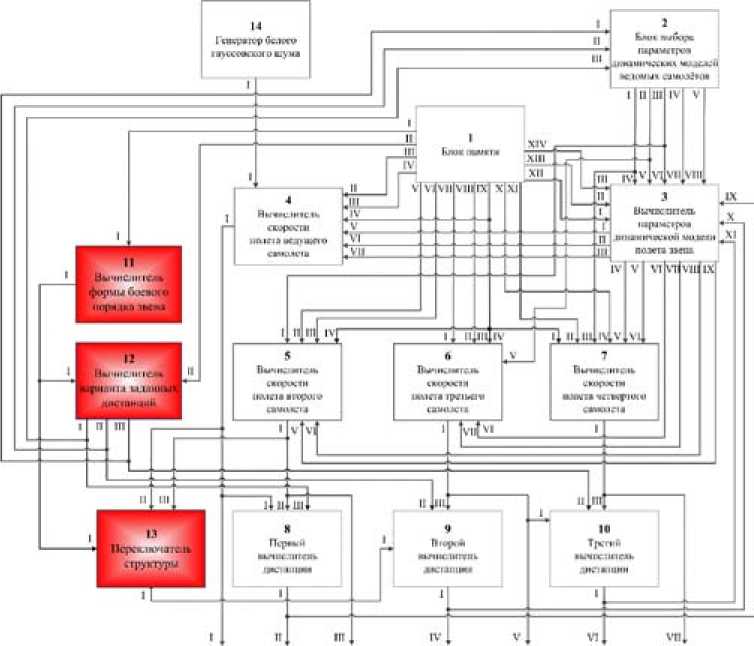
Рис. 8. Структура модели стационарного полета звена со сменой форм БП и выдерживаемых между самолетами группы дистанций

Fig. 8. Structure of model of stationary flight of a link with change of formation mode the distances maintained between planes of group

	0      1	и	0	0	а	0	а	0	0	it
	-A -^	*	"	*	п	°	о	»	0	о
	1        0	-1	0	0	0	0	0	0	0	0
	о о	0	0	1	0	0	0	0	0	0
	0    0	7?i	-Ри	~№?Г	а	о	0	0	0	о
Ai-Л-	■ 11 О	Л		О	а	- ]	0	О	О	it
	0    0	0	0	0	0	0	1	0	0	0

0  0  0  0 О | /ц Pt а_к ООО

о	О	О	0	0	а	1	а	о	-1	ti
о	о	0	О	0	0	I	а	0	0	1
0	fl	о	0	0	0	0	0

Рис. 9. Обобщенный вид матрицы коэффициентов

Fig. 9. Generalized view of a matrix of coefficients рое соответствует числу всевозможных наборов сменяемых состояний структуры звена, для рассматриваемого частного случая их число равно шести (по количеству вариантов форм БП и задаваемых дистанций).

После перехода от непрерывного времени к дискретному уравнение (26) примет вид

X(k + 1 ) = Ф (s)X(k) + GN(k) , X( 1 ) = X 0 ,                            (28)

где Ф( 5 ) - переходная матрица состояния, зависящая от формы БП и задаваемых дистанций;

G – матрица коэффициентов размерности 11×11;

N ( к ) = ( ni ( k),n 2 ( k ),n з ( k),n 4 ( k),n 5 ( k),n 6 ( k),n 7 ( k),n 8 ( k),n 9 ( k),n_w ( k),n_n(k ) ) T - матрица центрированных дискретных БГШ с единичными дисперсиями.

Для нахождения матрицы Ф( 5 ) необходимо решить следующее дифференциальное уравнение, полученное из (26) опусканием случайного слагаемого:

dXt ) = A (s ) X ( t ), X (0) = X 0.

Решением этого уравнения является матричная экспонента, определяемая матричным степенным рядом

Ф ( s ) = ex p { А ( s ) Т ) = I + А ( s ) Т + А ^- + АХТ ³ + к,               (29)

где I – единичная матрица; T – интервал дискретизации.

В результате согласования определения дискретного БГШ при переходе в выражении (26) от непрерывного времени к дискретному (28) матрица G будет иметь следующий отличный от нуля элемент:

g 22 = V^4а1°1 ^ •

Моделирование стационарного полета звена из четырех самолетов со сменой форм БП и задаваемых для выдерживания дистанций между самолетами группы проводилось при следующих исходных данных.

• 1.    Сменяемые формы БП – «пеленг» / «клин».

• 2.    Сменяемые варианты задаваемых дистанций:

• 3.    Начальное распределение вероятностей p 1 (0) = p 2 (0) = 0,5 форм БП.

• 4.    Интенсивности λ ₁₂ = 0,01 с^-1, λ ₂₁ = 0,007 с^-1 перестроения звена соответственно из БП «клин» в БП «пеленг» и обратно.

• 5.    Начальное распределение вероятностей q ₁(0) = 0,2, q ₂(0) = 0,3, q ₃(0) = 0,5 вариантов, задаваемых для выдерживания дистанций.

• 6.    Интенсивности μ ₁₂ = 0,0067, μ ₁₃ = 0,0059, μ ₂₁ = 0,0071, μ ₂₃ = 0,0053, μ ₃₁ = 0,0063, μ ₃₁ = 0,0067 смены вариантов, задаваемых для выдерживания дистанций.

• 7.    Постоянная составляющая скорости полета звена – V₀ = 200 м/с.

• 8.    Реальные численные значения характеристик скоростных флюктуаций ведущего самолета: τ₁ = 5,32 с; f₁ = 0,1 Гц; σ_v1 = 0,12 м/с.

• 9.    Для ВЩ рассчитаны параметры: α 1 = 0,188 с^-1; β 1 = 0,394 рад² с^-2; σ а1 = 0,079 м/с.

• 10.    Для вариантов задаваемых дистанций 60/200/400 м выбраны значения параметров ДМ ведомых самолетов в соответствии с табл. 1.

• 11.    Шаг дискретизации – T = 0,2 с.

• 12.    Число итераций – n = 1000.

• 13.    Моделирование проводилось при нулевых начальных условиях флюктуаций ведущего и ведомых самолетов звена, т. е.

1-й вариант – d 1 m _i , 2 = d 1 m _i , 3 = d 1 m _i , 4 = 60 м;

2-й вариант – d 2 m _i , 2 = d 2 m _i , 3 = d 2 m _i , 4 = 200 м;

3-й вариант – d3 mi, 2 = d3 mi, 3 = d3 mi, 4 = 400 м.

∆ V 1 (0)= ∆ V 2 (0)= ∆ V 3 (0)= ∆ V 4 (0)=0, а 1 (0) = а 2 (0) = а 3 (0) = а 4 (0) = 0.

Результаты моделирования одной реализации представлены на рис. 10–14.

Проверка полученной модели осуществлялась путем нахождения автокорреляционной функции (АКФ) ускорения ведомого самолета при варьировании параметрами его модели (рис. 15–20) для частного случая пары самолетов и фиксированных форме БП и варианте выдерживаемых дистанций. Характер полученных зависимостей не противоречит результатам летно-экспериментальных исследований [7].

Таблица 1

Table 1

№ самолета	Вариант дистанций
	1 – 60 м	2 – 200 м	3 – 400 м
2	α 21 = 0,1 с-1 β 21 = 0,2 рад2с-2 γ 21 = 0,01 рад2 с-3	α 22 = 0,216 с-1 β 22 = 0,47 рад2с-2 γ 22 = 0,017 рад2 с-3	α 23 = 0,25 с-1 β 23 = 0,6 рад2с-2 γ 23 = 0,001 рад2 с-3
3	α 31 = 0,2 с-1 β 31 = 0,3 рад2с-2 γ 31 = 0,02 рад2 с-3	α 32 = 0,256 с-1 β 32 = 0,57 рад2с-2 γ 32 = 0,027 рад2 с-3	α 33 = 0,3 с-1 β 33 = 0,7 рад2с-2 γ 33 = 0,002 рад2 с-3
4	α 41 = 0,3 с-1 β 41 = 0,4 рад2с-2 γ 41 = 0,03 рад2 с-3	α 42 = 0,296 с-1 β 42 = 0,67 рад2с-2 γ 42 = 0,037 рад2 с-3	α 43 = 0,4 с-1 β 43 = 0,8 рад2с-2 γ 43 = 0,003 рад2 с-3

Рис. 10. Смены форм БП

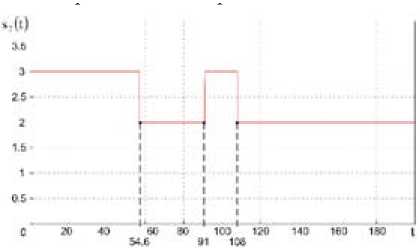
Рис. 11. Смены вариантов дистанций

Fig. 10. Changes of the formation mode forms

Fig. 11. Changes of the set options of distances

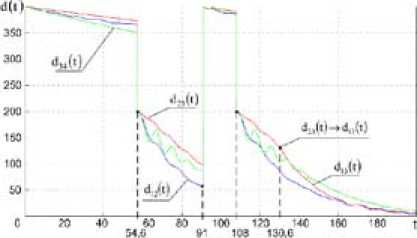
Рис. 12. Зависимость выдерживаемых дистанций в БП звена от времени

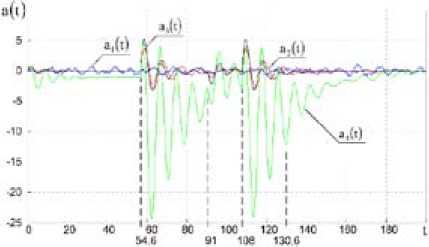
Рис. 13. Зависимость флюктуационных составляющих ускорений самолетов от времени

• Fig. 12.    Dependence of the maintained distances in link formation mode from time

• Fig. 13.    Dependence of flyuktuatsionny components accelerations of planes of a link from time

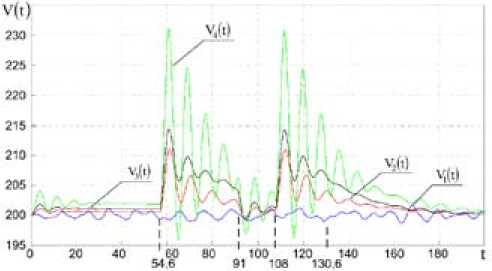
Рис. 14. Зависимость радиальных скоростей самолетов звена от времени

Fig. 14. Dependence of radial speeds of planes of a link on time

Таким образом, усовершенствована ДМ полета четырех самолетов для случая смены форм БП и дистанций в них, что позволяет повысить адекватность моделирования полета ГВЦ и получить новый квазиоптимальный алгоритм совместного сопровождения и распознавания ГВЦ в БРЛС истребителя, отличающийся повышенной точностью.

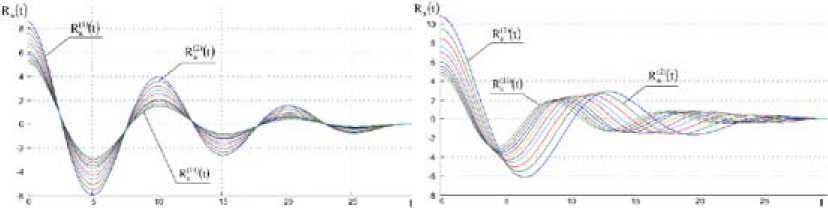
Рис. 15. Семейство АКФ ускорения ведомого самолета при варьировании параметром α 2 от 0,138 до 0,238 с шагом 0,01

Рис. 16. Семейство АКФ ускорения ВЩ самолета при варьировании параметром β 2 от 0,245 до 0,545 с шагом 0,03

• Fig. 15.    Autocorrelated function of acceleration of the conducted plane at variation by parameter from 0,138 to 0,238 with a step 0,01

• Fig. 16.    Autocorrelated function of acceleration of the leading plane at variation by parameter from 0,245 to 0,545 with a step 0,03

R.M

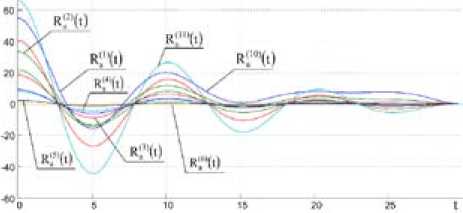
Рис. 17. Семейство АКФ ускорения ведущего самолета при варьировании параметром γ2 от – 0,015 до

0,015 с шагом 0,003

Fig. 17. Autocorrelated function of acceleration of the leading plane at variation by parameter from – 0,015 to

0,015 with a step 0,003

Алгоритм совместной фильтрации функционально связанных координат и распознавания состояния групповой воздушной цели на основе линейной модели с марковской структурой

Рассмотрим частный случай модели (1)–(4), когда динамика ФСК и БРЛС при их измерении описываются линейными уравнениями, а смена состояний ГВЦ и индикатор – марковскими цепями, вероятности перехода которых не зависят от фазовых координат.

Тогда выражения (1)–(4) примут следующий вид [5]: для динамики ФСК xk+1 = Ak (sk+1, sk) xk + Fk (sk+1, sk Xk,                                  (30)

для их измерений в БРЛС

Z k = C k ( S k ) X k + E k ( S k Z ,                                       (31)

для динамики состояний ГВЦ

qk (sk+11 xk, sk) = qk(sk+11 sk),

для идентификации состояния ГВЦ на основе «многогипотезного» подхода nk+i( rk+11 rk, sk+1) (33)

при известном законе распределения (5) возмущений и помех и заданных начальных условиях (6), где A k ( S k +1 , S k ), F k ( S k +1 , S k ), C k ( S k ), E k ( S k ) - известные матрицы детерминированных функций случайных аргументов ^S k и ^S k ⁺ 1 . ~

Отметим, что для решения частной задачи распознавания формы БП звена и варианта выдерживаемых в нем дистанций выражению (30) соответствует усовершенствованная модель (28) или эквивалентная ей система уравнений (16)-(23), а под (33) может пониматься статистическая характеристика индикатора формы БП, отличного по принципам функционирования от «многогипотезного».

Тогда на основе известных результатов теории систем со ССС с использованием метода двухмоментной параметрической аппроксимации [5] и применения в качестве индикатора состояния ГВЦ (структуры) многогипотезного оценивания [3] алгоритм квазиоптимальной совместной фильтрации ФСК и распознавания состояния ГВЦ, а в частности формы БП и варианта выдерживаемых в нем дистанций, примет вид (рис. 18)

p^k . ' ( s k ⁺¹⁾ Z q k ⁽ s k + 1 1 s k ) p^{k (} s k ) ,                                                   ⁽³⁴⁾

k xk+i(sk+1)=pk1 (sk^^k(sk. isk)pk(sk)Ak(sk+1,sk)xk(sk),                 (35)

k

Rk+1(Sk+1) = pk -Sk+1)Z Qk (Sk+1|Sk )pk (Sk ){Ak (Sk+1, Sk )Rk (Sk ) AT (Sk+1, Sk ) + sk

+ F k ( S k + 1 , S k ) G k F k ( S k + 1 , S k ) + [ ~ k ( S k + 1 ) - A k ( S k + 1 , S k ) X k ( S k ) ] x ^x x k ⁽ S k .,, ^- A k ⁽ S k + 1, S k ) x k ⁽ S _t ^{) ] T} } ,

P k + 1 ⁽ s k + 1 ) =

“ k + 1 ⁽ s k + 1 ) , Z « k + i ⁽ s k + 1 )

s k + 1

xk+1( Sk+1) = ~k+1( Sk+1) + Rk+1( Sk+1) CkT+1( Sk+1)®-+1( Sk+1)A k+1( Sk+1),

^ ks                          \CT      A0-1     \CA k+1(Sk+1)   ^k+1(Sk +1) ^k+1(Sk+1)^ k+1(Sk+1)W k+1(Sk+1)^ k+1(Sk+1)^ k++1(Sk +1), (av)

уд ak+1(sk+1) = pk+1(sk+1 )nk(rk+1 I rk, sk+1)[det ® k+1(sk+1)]     exp[-hk+1(sk+1)],

0 k+1( Sk+1) = Ck+1( Sk+1) Rk+1( Sk+1) CL1( Sk+1) + Ek+1( Sk+1)Qk+1 Ek+1( Sk+1), h (Sk+1) = ^ ^k+1 (Sk+1)0 k+1 (Sk+1)A k+1( Sk+1),

A k+1( Sk+1) = zk+1 - Ck+1( Sk+1)~ (Sk+1),

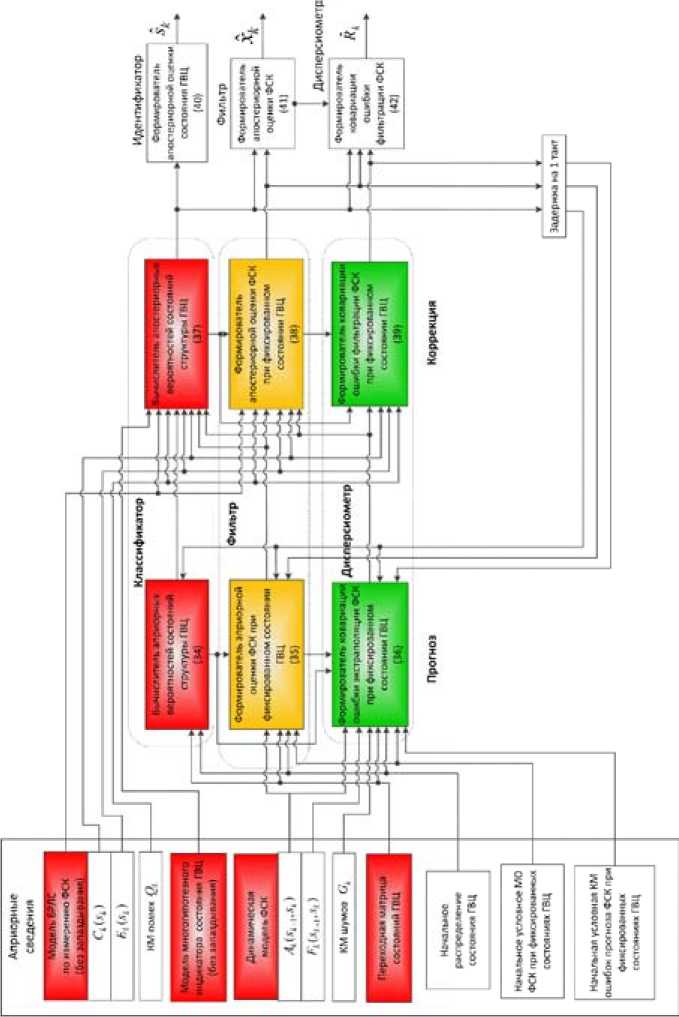
Fig. 18. Block diagram of quasioptimal algorithm of phase coordinate and clustered air target state где Рк+1(sk+1) и pk+1(sk+1) - соответственно прогнозируемая на один шаг дискретности вперед иапостериорная вероятности нахождения ГВЦ в состоянии sk+1; ~

X k + 1 ( S k + 1 ) и X k + 1 ( S k + 1 ) — соответственно прогнозируемая на один шаг дискретности вперед условная оценка и апостериорное условное математическое ожидание (МО) ФСК при фиксированном состоянии ГВЦ; ~

Rk + 1( Sk + 1) и R k + i ( S k + i ) - соответственно прогнозируемая на один шаг дискретности вперед и апостериорная условные ковариационные матрицы (КМ) вектора ФСК при фиксированном состоянии ГВЦ;

G k , Q k — КМ соответственно векторов шумов возбуждения ^ _k и помех Z _k ;

® k +i ( S k +1 ) — условная КМ измерения при фиксированном состоянии ГВЦ.

При этом идентификация распознанного состояния ГВЦ и безусловные оценки ФСК x _k и R k вычисляются по формулам:

оптимальная по критерию максимума апостериорной вероятности оценка состояния ГВЦ sk = argmax pk (sk);                                                  (40)

s математическое ожидание ФСК

xk = Y xk(sk)P(sk);                                                  (41)

sk ковариационная матрица ФСК

'■? R“s ■/“l■*

Результаты моделирования [8, 9] аналогичного алгоритма, основанного на моделях со ССС, в задаче оценивания дальности при сопровождении маневренной воздушной цели в сравнении с алгоритмом, основанным на линейной калмановской фильтрации, свидетельствуют о повышении точности фильтрации.

Заключение

Таким образом, разработан алгоритм совместной фильтрации радиальных функционально связанных координат самолетов звена и распознавания формы их боевого порядка и варианта выдерживаемых дистанций.

Для этого построена обобщенная модель системы «ГВЦ – истребитель» как системы со случайной скачкообразной структурой, позволяющая устранить ряд ограничений линейных моделей при калмановской фильтрации и применять результаты теории систем со ССС в интересах совершенствования алгоритмов совместного оценивания ФСК и состояния групповой воздушной цели.

Усовершенствована динамическая модель полета звена самолетов для случая смены форм БП и дистанций в них. Новым признаком, обладающим существенным отличием, является случайная и скачкообразная смена структуры модели, которая позволяет повысить адекватность описания динамики полета ГВЦ.

Синтезирован алгоритм совместной фильтрации ФСК и распознавания состояния ГВЦ на основе линейной модели с марковской структурой, отличающийся от известных использованием дополнительных априорных сведений о динамике распознаваемых состояний ГВЦ, а также комплексированием информации, поступающей от измерителей и индикаторов.

В совокупности реализация полученных результатов на борту истребителя позволит расширить функциональные возможности БРЛС и повысить ее точностные характеристики по сопровождению и распознаванию групповых воздушных целей.

Дальнейшим направлением исследований по оптимальной обработке информации о ГВЦ в БРЛС истребителя является синтез на основе моделей со ССС и с учетом перспективных алгоритмов [8-11] системы оптимальных и квазиоптимальных алгоритмов совместного траекторного сопровождения ГВЦ и распознавания таких ее состояний, как численный и типовой (классовый) составы, характер полета по принципу «стационарный полет – маневр группой – маневр в группе», вид оказываемого информационного противодействия, а также количество пущенных ракет.

Работа выполнена при поддержке РФФИ (проект 16-08-00464а).