Алгоритм стеганографического скрытия информации на основе пространственной деформации фрагментов полноцветных изображений

Компьютерная стеганография представляет широкий набор методов скрытного встраивания защищаемых данных в структуру других данных, называемых контейнерами, которые могут храниться в открытом виде или передаваться по незащищённым каналам. Среди потенциальных областей практического применения методов стеганографического скрытия информации (ССИ) следует отметить их использование в DRM-системах при реализации технологий создания цифровых водяных знаков и «отпечатков пальцев» для защиты прав авторства и контроля за незаконным распространением защищаемого цифрового контента, скрытое аннотирование разнородной мультимедиа информации, а также возможность использования в системах аутентификации для подтверждения подлинности цифровых документов [1, 2].

К числу наиболее распространённых методов компьютерной стеганографии относятся методы, основанные на использовании свойств избыточности визуальной и аудио информации. Среди наиболее распространённых на сегодняшний день классов алгоритмов ССИ в контейнеры графических форматов необходимо выделить следующие:

– алгоритмы разделения битовых слоёв растровых изображений носителей на сегменты по уровню сложности с последующей заменой шумовых областей битами сообщения (BPCS-алгоритмы) [3];

– алгоритмы модификации младших бит цветовых значений пикселей, предусматривающие псевдослучайный выбор пикселей носителя, адаптивный выбор количества младших бит пикселей для модификации, а также коррекцию статистических характеристик результирующего контейнера [4, 5];

– алгоритмы модификации младших бит спектральных коэффициентов изображения-контейнера с псевдослучайным их выбором и коррекцией статистик заполненного контейнера для минимизации вероятности детектирования скрытых данных [6, 7];

– алгоритмы модификации таблиц квантования JPEG [8];

– алгоритмы модификации палитры цветов [9].

Следует отметить, что практически все рассмотренные алгоритмы при внесении скрываемой инфор- мации реализуют искажения контейнера, носящие аддитивный или мультипликативный характер. К числу основных недостатков приведенных алгоритмов ССИ в изображения можно отнести сравнительно низкую стойкость по отношению к типовым операциям преобразования маркированных файлов, «алгоритмический» характер процедуры встраивания информации, при котором реализуются логически определённые последовательности операций на заранее известном подмножестве элементов контейнера. Их применение зачастую приводит к изменению статистик заполненного контейнера и, как следствие, делает возможным успешное использование стегоанали-тических атак. Применяемая в некоторых алгоритмах коррекция статистических характеристик контейнера требует дополнительных вычислительных затрат и не всегда позволяет обеспечить незаметность ССИ с точки зрения стегоанализа.

В данной работе описывается подход к ССИ, основанный на внесении относительно низкочастотных малозаметных деформирующих искажений во фрагменты полноцветных изображений-контейнеров и использовании свойства корреляции цветовых каналов изображений для последующего извлечения скрытых данных. Отличие предлагаемого алгоритма ССИ от известных, главным образом, заключается в реализации нестандартного способа внесения незначительных искажающих изменений графического контейнера, которые носят не аддитивно или мультипликативный характер, а основаны на плавной эластичной деформации непересекающихся фрагментов контейнера. При этом обеспечивается возможность осуществления «нецелочисленных» сдвигов координат опорных точек деформируемых областей изображения за счёт привлечения специальных процедур аппроксимации цифрового изображения и его представления в виде непрерывной функции пространственных координат. Как показали предварительные эксперименты, а также представленные ниже результаты, при реализации такого подхода факт ССИ не обнаруживается при первичном визуальном анализе, а также с привлечением известных статистических стеганографических атак, ориентированных на классические схемы стегоскрытия.

Процедура восстановления ранее скрытой информации, основанная на анализе нарушенной корреляции цветовых компонент фрагментов заполненного контейнера, в предлагаемом алгоритме реализуется с использованием аппарата искусственных нейронных сетей. Адаптивный характер, способность к дообучению для работы с графическими контейнерами, имеющими различные статистические характеристики, позволяет рассматривать нейронные сети в качестве универсального стеганографического декодера.

Следует отметить, что идея использования нейронных сетей в приложениях стеганографии на сегодняшний день является весьма актуальной. Анализ целого ряда публикаций позволяет сделать вывод, что нейронные сети используются в качестве декодеров, классификаторов и инструментов принятия решений о наличии в контейнере скрытой информации [10– 12]. Однако следует отметить, что предложенный в статье вариант применения нейронных сетей для восстановления скрытой информации в известных работах не рассматривался.

1.    Алгоритм встраивания информации

В общем виде задача стеганографического информационного скрытия формулируется следующим образом [1]. Требуется для множества возможных контейнеров Z , скрываемых сообщений D и стеганографических ключей K реализовать преобразования вида:

F : ZxD xK ^ Z , V z e Z, z e Z : ||z - z|| ^ min ,

F 2 : Z x K ^ D , V d e D , d e D : || d - d || ^ min . (1)

При построении прямого F ₁ и обратного F ₂ стеганографических преобразований обязательным условием является минимизация искажающих изменений заполненного контейнера z ɶ , а также минимизация ошибок при извлечении сообщения d . Также для систем создания и использования цифровых водяных знаков (ЦВЗ) выдвигается требование робастности встроенных сообщений к возможным искажениям £ маркированного контейнера: || d - F 2 ( z + £ , k )|| ^ min . В качестве сообщения d без ограничения общности всегда можно рассматривать двоичную (битовую) последовательность.

Как известно, любой алгоритм ССИ основан на внесении незначительных изменений в структуру файла-контейнера либо на изменении его статистических свойств таким образом, чтобы, зная характер вносимых изменений, можно было сформировать решающие правила (детекторы), позволяющие с той или иной степенью достоверности обнаруживать модификации, внесённые в процессе ССИ.

В качестве вносимых изменений, кодирующих биты скрываемой информации ( d ), далее предлагается использовать пространственную деформацию фрагментов полноцветных растровых изображений ( z ), выполняемую для одной из цветовых компонент про- странства RGB. Основная идея выполняемой обработки состоит в том, чтобы при извлечении на основе обучаемого решающего правила выявить наличие и параметры вносимых деформаций, и базируется на следующем. Характерной особенностью полноцветных изображений фотографического характера с глубиной цвета не менее 16 бит/пиксель является наличие локальной зависимости между составляющими градиента отдельных цветовых каналов. Так, в работе [13] отмечается, что объекты на цветных изображениях коррелируют между собой (совпадают по положению контуров и текстурным перепадам) в цветовых каналах. Незначительное локальное нарушение корреляции цветовых компонент пикселей (например, в цветовом пространстве RGB) можно использовать в интересах реализации стеганографических преобразований для встраивания и декодирования информации в контейнер-изображение.

В качестве базового метода искажения выбранных цветовых плоскостей двумерного изображения для реализации процедуры ССИ нами предлагается использовать метод эластичной деформации решётчатой функции с использованием аппроксимации на основе радиальных базисных функций (radial basis function, RBF) [14,15]. Среди преимуществ RBF-метода деформации перед известными сеточными методами [16,17] и методами многомерной интерполяции [18] следует отметить возможность точной плавной интерполяции участков растра, учёт изменения координат лишь заданных опорных точек (узлов) без привязки к сетке, возможность использования функций радиального базиса различной гладкости.

Математическая модель процесса внесения деформирующих искажений (ДИ) для исходной функции f ( x ₁,..., x_n ) n аргументов определяется следующим соотношением:

f ( Х 1 + Г 1 ( X i ,.., X n ),.., X n + r ( X i ,.., X n )) =

= f(ui( X1,.., Xn ),.., un (X1,.., Xn )) = f(u (X)) = g (X1,.., Xn ) , где g(x1,...,xn) – результирующая деформированная функция; ri (X1,..., Xn), i = 1, n - функции вносимых деформирующих искажений по каждой координате, которые могут носить детерминированный или стохастический характер. Обозначив r(x) = (r1(x),...,rn (x))T , перепишем (2) в виде:

f ( x + r ( x )) = f ( u ( x )) = g ( x ). (3)

При реализации процесса внесения ДИ на основе (3) возникает ряд особенностей. Первая из них заключается в том, что область определения деформированной функции g (x1,^ xn) не должна выходить за пределы области определения исходной функции f (x1,^ xn). Данное условие исключает возможность возникновения артефактов при выходе аргументов в случае внесения ДИ за пределы области определения исходной функции. Для гарантированного обеспече- ния выполнения этого условия можно использовать ограничивающие значения функции u(x) по краям области определения исходной функции маски u(x) = x + h(x)r(x). Функции h(x) должны стремиться к нулю на границах области определения и к единице в её центре. В качестве них могут быть использованы гауссианы с соответствующим образом подобранными параметрами.

Вторая особенность реализации процесса внесения ДИ на основе (3) состоит в следующем. В случаях, когда исходная функция f ( x ) является решётчатой функцией дискретных аргументов, т.е. задана на многомерной дискретной сетке (например, в случае деформации цифровых растровых изображений), прямое применение (3) невозможно. В данном случае для обеспечения возможности модификации аргументов f ( x ) при внесении в них ДИ произвольного характера необходимо предварительно выполнять интерполяцию и её представление в виде функции f ( x ) непрерывных аргументов. Далее вносятся деформирующие искажения путём подстановки r ( x ) в аргументы f ( x ) . В результате получается деформированная функция непрерывнозначных аргументов g ( x ) , которая далее дискретизируется. В результате формируется новая решётчатая функция дискретных аргументов g ( x ) .

При реализации предлагаемого алгоритма стеганографического скрытия данных осуществляется независимая деформация блоков изображения фиксированного размера. Для соседних блоков граничные пиксели являются общими. Для простоты набор пикселей, описывающих деформируемый блок изображения размерностью w х h , запишем в виде вектора P = ( P 1 ,P 2,... P n ), где P j = ( x j , y j ), j = 1, n , n = wh . Для аппроксимации блока пикселей непрерывной функцией вычисляется интерполирующая функция в виде:

n f (x, У) = E WjU (| Pj — (x, У )||) + Ф( x, У), (4) j=1

где wj – неизвестные коэффициенты, которые требуется найти; U (rij ) задаёт вид радиальных базисных функций, rij = |P - Pj|| = ^(x - j +(y, - yj )2 - расстояние между точками с координатами (xi , yi ) и (xj,yj), i, j = 1,n ; ф(x,y) = ф1 + фxx + фyy - полином, вводимый в (4) в случае использования в качестве U сплайнов «тонкой пластины» или мультиквадратич-ных RBF-функций [19, 20]. На практике в качестве U часто применяются функции вида гауссиана (U(r) = e"r2, a> 0), мультиквадратичные и обрат ные мультиквадратичные функции (U(r) = V1 + r2, u (r) = ( Vw )-1),

сплайны «тонкой пластины»

( U ( r ) = r ² log( r )), ядра Вендланда. При реализации алгоритма стеганографического встраивания данных рассматривались два варианта RBF-функций: U ( r ) = e~^{r 2 0} , где о - параметр влияния RBF-функций, и U ( r ) = r ² ln( r ).

Элементам суммы (4) соответствуют центры RBF-функций с координатами x_j , y_j . При наличии в (4) полинома ф коэффициенты w j должны подчиняться условиям:

nn  n

E w j = ⁰ , E w j x j = ⁰ , E wy = ⁰.

j = 1                j = 1                    j = 1

Вектор W = ( w 1 , . w_n ) и коэффициенты полинома ( ф 1 , ф x , ф _y ) определяются из системы уравнений, записываемой в матричной форме в виде

A = K^XY ,

где

/ ,          А т I KB

A = (W | ф1 фx фy) , L = I B^O

K =

I 0

^U ( r 21 )

I U ( r n 1 )

1 1 x 1

^U ( ^r 12 ) 0

^U ( ^rn 2 ) ^y . , У п )

^{U ( r} 1 n ) )

U ( r 2 n )

⁰ )

O – нулевая матрица размером 3×3; Y = ( V |0 0 0) ^T ,

V = (v1, ..., vn), vi – значения решётчатой функции дис- кретных аргументов в координатах (xi, yi ) .

На практике получаемые в (5) системы уравнений не всегда могут иметь стандартное решение из-за плохой обусловленности невырожденной матрицы L [20]. В этих случаях применяются методы регуляризации. Например, используют расчёт псевдообратной матрицы A = L ⁺ Y (где L ⁺ - псевдообратная матрица к L ) или регуляризацию по А.Н. Тихонову [21]. В последнем случае решение имеет вид

A = (XI + LTL)-1 LT (Y - LA0), где I - единичная матрица размером (n + 3) х (n + 3); % - параметр регуляризации, A0 - априорное решение. При регуляризации чем больше %, тем лучше обусловленность и ближе решение к априорной оценке A0 , но дальше от решения исходной некорректной задачи. Исходя из этих соображений, параметр % должен принимать промежуточные значения, определяемые эмпирическим путём или при помощи дополнительного анализа. Если в качестве A0 использовать нулевую матрицу, то регуляризация будет проводиться без учёта априорного решения [15].

В простейшем случае искажения контейнера выполняются путём внесения плавной сдвиговой деформации центральной части каждого фрагмента вдоль одной из осей или по диагонали на заданное значение амплитуды сдвига Δ, измеряемой в единицах пикселей. Необходимо отметить, что предлагаемый подход позволяет вносить деформирующие искажения при любых значениях амплитуды искажений Δ, в том числе нецелочисленных. Пример деформации фрагмента изображения «Lena.bmp» с использованием в качестве RBF-функции сплайнов «тонкой пластины» приведен на рис. 1а, б. На исходном и искажённом изображениях дополнительно показана сетка, в координатах узлов которой задавались опорные точки, относительно которых производилась деформация (задают решётчатую функцию дискретных аргументов). Для каждого узла сетки деформация представляла из себя односторонний сдвиг в случайном направлении (вертикально-горизонтальном или диагональном) с максимальной амплитудой Δmax=3 пикселя. Следует отметить, что вносимые в процессе деформации растра искажения носят низкочастотный характер, что является важным аспектом при реализации стегоал-горитмов, потенциально устойчивых к высокочастотным искажениям контейнера-изображения. Что касается требования минимизации искажающих изменений стеганографического контейнера, то при амплитуде деформации Δmax≤1 на изображениях с невыраженной ре- гулярной структурой визуально определить наличие

фрагмент «деформированного» изображения, максимальная амплитуда деформации Amax=3 (б)

Далее с учётом особенностей предлагаемого алгоритма внесения ДИ для реализации ССИ использовались непересекающиеся блоки контейнера, а не изображение целиком, и проводилась независимая деформация отдельных цветовых компонент в рамках каждого блока в различных направлениях, соответствующих значениям элементов битовой последовательности. Информационная ёмкость предложенного алгоритма, определяемая отношением объёма доступного пространства сте-госкрытия к общему объёму контейнера, невелика. В случае встраивания одного бита информации в каждый деформируемый блок контейнера, информационная ёмкость будет определяться отношением числа модифицируемых блоков контейнера к его объёму в битах. Так, для несжатого полноцветного растрового изображения размером 1600×1200 пикселей, содержащего 30000 не-пересекающихся блоков размерностью 8×8 пикселей, каждый из которых используется для встраивания одного бита сообщения, информационная ёмкость алгоритма составит 6,51∙10-4.

При реализации «блочного» варианта алгоритма скрывающее информацию преобразование F1 можно записать в виде:

F i ( z ⁽ i ) , d i ) =

J z ^{( 1}) , d i = 0 [ z i ) , d i = 1

i = 1, N ,

где N – длина встраиваемой последовательности в битах, z(1) =( zR1) | zRi) | zR1) )e z, 'z - непересекающие- ся блоки пикселей заданного размера wх h , которые не подвергаются модификации,

■z^¹ ) = ( z R' ) | z Ri ) | z B¹ ) ) e z , i = 1, N - блоки пикселей, полученные в результате пространственной деформации их синих цветовых плоскостей z_B ^{( i )} . Выбор для модификации синих цветовых плоскостей блоков обусловлен физиологическими свойствами человеческого зрения и направлен на минимизацию визуальных искажений маркированного контейнера. По аналогии с алгоритмом JPEG рассматривались квадратные блоки пикселей размерностью 8×8 пикселей. Для простоты длина встраиваемого сообщения выбиралась не больше доступного пространства стегоскры-тия, определяемого общим количеством непересе-кающихся блоков заданного размера на изображении.

В общем случае деформация синей цветовой плоскости в блоке изображения выполняется путём сдвига синей компоненты блока на заданный шаг Δ вдоль одной или нескольких осей фрагмента контейнера z_B ^{( i )} в низкочастотном спектре. Преобразования производятся над элементами контейнера, представленными в вещественной форме. После деформации значения пикселей дискретизируются.

При увеличении модифицированных изображений цветовых плоскостей на контрастных областях растра можно наблюдать артефакты встраивания – незначительные изломы границ объектов. В то же время при объединении цветовых плоскостей и рассмотрении полноцветного растра (рис. 2 г ) визуально определить факт деформации (для малых Δ max ≤1) практически невозможно.

2.    Алгоритм извлечения информации

Для реализации восстанавливающего скрытые данные преобразования F 2 использовалась однослойная нейронная сеть (НС) прямого распространения с линейной передаточной функцией (рис. 3), реализующая двухальтернативное решающее правило (на выходе сети восстанавливается двоичная последовательность данных d ).

а)

Рис. 2. Увеличенный фрагмент исходного изображения «Lena.bmp» (синий цветовой канал) (а); фрагменты «блочно» деформированного изображения (синий цветовой канал) с амплитудой деформации Δ_max = 0,5 (б), Δ_max = 1 (в) и Δ_max =2 пикселя (в), размер блоков 8×8; фрагмент изображения, сформированного в результате объединения деформированного синего цветового канала с исходными (красным и зелёным) при Δ_max = 1

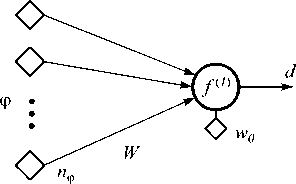
Рис. 3. Нейронная сеть, реализующая восстановление скрытой информации

Результаты предварительных экспериментов показали, что для формирования обучающей выборки, в максимальной степени отражающей корреляционные связи нетронутых (R,G) и деформированных (B) цветовых плоскостей, целесообразно использовать разности их градиентов. Дополнительно для уменьшения артефактов стеганографического кодирования эмпирически задаётся порог 10 <т<120 , определяющий допустимые максимальные значения уровня градиента для немодифицируемых R и G цветовых компонент блока. В этом случае очередной i -й блок контейнера выбирается для модификации, если выполняется условие max ( max ( V z R' ) ) , max ( V z R ) ) ) < т .

Матрица обучающих данных НС определялась в виде Ф = { ф_рф 2 ,..., ф м } , где

фI = (фR)(0,0) фс)(0,0)'"фд)(w-1, h-1) фс)(w-1, h-1)) ,

i = 1, M , M - объём обучающей выборки, определяемый числом блоков, в которые производится встраивание информации. Элементами вектора ф i являются выписанные по столбцам элементы матриц разности градиентов (с центрированием) цветовых плоскостей i -го блока:

ф£ ) = V z^{( i} ') - V z ( i ') ф ⁽/) = V z ( i ) - V z ( i' ) R R B G G B

V z R > ( j , l ) = V z R ( j , l ) - m R^

V z Ri ) ( j , l ) = V z Ri ) ( j , l ) - m Ri ) ,

V z B ) ( j , l ) = V z B ) ( j , l ) - m Bi ) ,

V z R ) = у/ ( S x * z R ) /255 ) 2 + ( S x * z R ) /255 ) 2 ,

V z Ri ) = ( S x * z R ) /255 ) 2 + ( S x * z R ) /255 ) 2 ,

V z R ) = J ( S x * z B ) /255 ) 2 + ( S x * z Bi ) /255 ) 2

(* обозначает двумерную операцию свертки), wh mRi) =(wh)-1 ЕЕVzR) (j,l), j=1 l=1

wh mRi) =(wh)-1 ЕЕVzRi) (j,l), j=1 l=1

wh mBi) =(wh)-1 ЕЕVzB) (j,l). j=1 l=1

Для вычисления градиента использовались стандартные ядра дискретного дифференциального оператора Собеля размером 3×3 s_x , s_y . Количество входных контактов сети n _ф = 2 wh определялось как удвоенное число пикселей обрабатываемого блока изображения. Ожидаемые на выходе сети значения определялись компонентами целевого двоичного вектора-сообщения d = ( d 1, d 2,... d_M ) , где d i = { - 1, + 1 } , i = 1, M .

Матрица входных данных для тестирования обученной НС формировалась в виде Ф = {ф1,ф2,.фq} , где векторы фi, i = 1, Q содержат элементы матриц разности градиентов цветовых плоскостей блоков тестового изображения, Q– объём тестовой выборки, определяемый числом блоков контейнера, в которые производилось встраивание информации. Получаемые на выходе сети данные обозначались как d = (d1,d2,.dQ), где di ={-1,+1} , i = 1,Q .

При практическом использовании НС для реализации правила восстановления ранее скрытых данных по возможности следует исключать случаи переобучения сети. Эффект переобучения наблюдается при «индивидуальном» (контентно-зависимом) обучении НС – с использованием выборки обучающих данных малого размера, сформированной на основе фрагментов одного графического контейнера. При последующем использовании такой сети для восстановления информации, скрытой в контейнеры с отличающимися характеристиками, возможно значительное снижение достоверности процедуры восстановления данных и получение некорректных результатов. Следует, однако, отметить, что это лишь возможный частный случай практического использования алгоритма для конкретного контейнера. С целью улучшения репрезентативности приводимых в статье результатов при проведении тестирования обучающая выборка для НС, реализующей восстановление ранее скрытой информации, формировалась на основе фрагментов нескольких различных изображений из тестовых наборов [22, 23]. Впоследствии обученная сеть использовалась для извлечения данных из других изображений, не участвовавших в обучении.

• 3.    Экспериментальные исследования уровня искажения контейнера и достоверности восстановления скрытых данных

  Экспериментальный анализ разработанного алгоритма в части оценки искажающих изменений контейнера и достоверности восстановления скрытых данных проводился с использованием полноцветных несжатых изображений из известных наборов Kodak Lossless True Color Image Suite [22] и TESTIMAGES [23]. Разрешение тестовых изображений варьировалось от 300×300 до 1200×1200 пикселей. Тестирование стегоалгоритма проводилось как по изображениям, фрагменты которых содержались в обучающем множестве восстанавливающей данные НС, так и по изображениям, не участвовавшим в обучении НС. Основным критерием предварительной оценки уровня искажений контейнера являлась среднеквадратическая ошибка (СКО)

w , h                     ₂

msE xy = ( wh ■ £ ( X,._a- y J , i = i,j = 1

где X – исходное изображение, Y – изображение, содержащее скрытно встроенную информацию, w и h – ширина и высота изображения. Вероятность ошибки при извлечении информации определялась как P_err = n_err / M , где n_err – количество ошибочно восстановленных НС бит.

На рис. 4 приведены зависимости среднеквадратической ошибки искажения контейнера и вероятности ошибки восстановления скрытой информации от значений амплитуды деформации в блоках изображения для RBF-функций U ( r ) = r^-r 2 /2 ^е2 , параметр влияния RBF-функции о = 0,85 (рис. 4 а , б) и U ( r ) = r 2 ln( r ) (рис. 4 в , г ).

Соотношения были получены для следующих условий: размер обрабатываемых блоков контейнера – 8×8 пикселей, амплитуда деформации – 0,5≤Δ≤3, объём выборки для обучения нейронных сетей P1 = 4000, объём тестирующей выборки P2 = 10000, число эпох обучения T = 5000, порог для уровня градиента, при превышении которого встраивание информации не производится, т = 30. Для извлечения данных использовалась однослойная НС с линейной передаточной функцией, реализующая двухальтернативное решающее правило. На графиках используются следующие обозначения: mse_train1,2 – СКО искажения контейнера при тестировании алгоритма на данных, используемых для обучения НС, mse_test1,2 – СКО искажения контейнера при тестировании на данных, не участвовавших в обучении НС, perr_train1,2, perr_test1,2 – вероятности ошибки восстановления скрытой информации при тестировании на данных используемых и не используемых для обуче- ния НС соответственно. Индексы в обозначениях характеризуют варианты деформации: 1 – деформацию содержимого блока по двум направлениям (симметричное растяжение по оси OX или OY), 2 – деформацию в одном направлении (сдвиг на заданный шаг А по одной из осей).

( СКО искажения контейнера ).

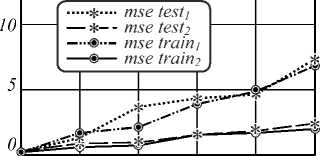
Рис. 4. Зависимости среднеквадратической ошибки искажения контейнера (а, в) и вероятности ошибки восстановления скрытых данных (б, г) от значения амплитуды деформации для RBF-функций двух видов

Как показали результаты экспериментов, с увеличением амплитуды деформации вероятность ошибки восстановления скрытой информации убывает до 0,5 % для первого и до 1 % для второго варианта деформации (для RBF-функции вида Гауссиана) и до 0,3 % и 2% (для сплайнов «тонкой пластины») при проведении тестирования на данных, не участвовавших в обучении сети и значении амплитуды А = 3. Одновременно с этим СКО искажения маркированного контейнера возрастает до 2 и 7,5 соответственно (для Гауссовых RBF-функций) и до 3,5 и 12 (для сплайнов «тонкой пластины»). Следует отметить, что критерий предварительной оценки ошибок – СКО (впрочем, как и все остальные математические критерии) не может соответствовать всем аспектам восприятия искажений человеком и не отражает наличие возможных структурных артефактов, возникающих в результате стеганографического скрытия информации, поэтому после внесения деформации в блоки контейнера желательно всегда визуально оценивать результат.

Существенно повысить достоверность восстановления информации возможно за счёт обучения и использования НС, реализующих оператор F ₂, индивидуально для каждого маркируемого контейнера. В этом случае параметры обученной сети будут являться стеганографическим ключом. При тестировании стегоалгоритма на данных, используемых для предварительного обучения НС, независимо от вида функции U в (4) вероятность ошибок извлечения информации не превышает 1 % для значений ∆ ≥ 1,5 .

• 4.    Экпериментальные исследования устойчивости скрытых данных к возможным искажениям заполненного контейнера, а также к некоторым статистическим стегоатакам

Для исследования устойчивости предложенного алгоритма стеганографического информационного скрытия были проведены эксперименты в части оценки вероятности восстановления ранее скрытых данных из заполненных контейнеров, подвергшихся искажениям в виде искусственного зашумления импульсным шумом (плотностью η от 5 до 30 %), медианной и сглаживающей фильтрации, преобразованиям яркости.

Относительная устойчивость встроенной информации была показана при добавлении к заполненным контейнерам импульсного шума небольшой плотности. Для зашумлённых носителей из тестовых наборов, имеющих 100% заполнение и сформированных при использовании оптимальной с точки зрения минимизации визуальных искажений значений амплитуды деформации ∆max ≤ 2 для блоков контейнера размером 8×8 пикселей, деформируемых по двум направлениям, Гауссовых RBF-функций и порогового значения уровня градиента τ = 30 были получены следующие усреднённые по реализациям (разным контейнерам) значения вероятности ошибок восстановления данных. Вероятность ошибки извлечения информации для контейнеров, участвовавших в обучении составила perr_train1 ≈ 4,5 % при η = 0,05 , perr_train1 ≈ 1 1% при η = 0,1, perr_train1 ≈ 26,5 % при η = 0,3 . Для тестовых контейнеров, не участвовавших в обучении НС perr_test1 ≈ 6,5 % при η = 0,05 , perr_test1 ≈ 16 % при η = 0,1, perr_test ≈ 29 % при η = 0,3 . Полученные значения показывают возможность уверенного восстановления встроенной информации (с незначительными ошибками) при небольшой плотности вносимого импульсного шума (<0,15). При большей доле искажённых шумом пик- селей ошибки восстановления информации можно считать неприемлемыми.

Устойчивость встроенных данных к изменению яркости и нормализации цветовых гистограмм (авто-урови) заполненного контейнера была показана для больших значений амплитуды деформируемых блоков Δ≤2 (размер блока – 8×8, Гауссовая RBF-функция, τ=30). Вероятности ошибки восстановления для протестированного множества изображений с изменённой яркостью или прошедших нормализацию в среднем соответствовали представленным на рис. 4 б , г значениям, вычисленным для неискажённых контейнеров. Следует отметить, что при малых значениях амплитуды деформации Δ≤1 после применения яркостной коррекции вероятность ошибочного восстановления устойчиво возрастала до 30 % и более.

Встроенные предложенным способом данные оказались неустойчивы к медианной фильтрации. Так, корректно восстановить встроенную информацию не удаётся (perr_test 1,2 ≈50%), после применения медианного фильтра со скользящей апертурой размером 3×3 пикселя к типовым контейнерам из тестовых наборов, имеющих 100% заполнение и сформированных для значений амплитуды деформации ∆ _max ≤ 2 , блоков размером 8×8 пикселей, Гауссовых RBF-функций, порога уровня градиента τ = 30 . Аналогичные результаты наблюдаются после применения низкочастотной пространственной фильтрации, реализуемой с помощью операции сглаживания. Даже в случае выбора малой размерности скользящей апертуры (3×3) незначительное размытие границ объектов на изображении приводит к нарушению локальной зависимости между составляющими градиента отдельных цветовых каналов в деформированных блоках контейнера, что делает невозможным дальнейшее корректное восстановление скрытых данных. Средние значения ошибки восстановления бинарного сообщения для «сглаженных» контейнеров, не участвовавших в обучении НС, с параметрами алгоритма: ∆ _max ≤ 2 , размером блока 8×8 пикселей, порогом уровня градиента τ = 30, составили perr_test_1,2 ≈ 50%. Следует отметить, что увеличение размеров деформируемых блоков с одновременным увеличением значения амплитуды ∆ _max (в качестве возможного сценария повышения устойчивости к медианной и усредняющей фильтрации), на наш взгляд, не имеет практической ценности, поскольку получаемые в результате изображения будут иметь видимые артефакты на границах контрастных объектов, что противоречит базовым принципам стеганографии о визуальной незаметности скрытой информации.

Одним из основных ранее заявленных достоинств предложенной схемы ССИ является сохранение после встраивания информации большинства статистических характеристик контейнера, традиционно нарушаемых классическими стегоалгоритмами (распределения младших бит, частоты переходов битовых значений и т.п.). Для демонстрации устойчивости пред- ложенного алгоритма к статистическим атакам, направленным на анализ классических алгоритмов ССИ, использовались критерий хи-квадрат [1], определяющий схожесть теоретических и эмпирических гистограмм цветовых компонент исследуемого контейнера, и разностный стегоанализ на основе двойной статистики (RS-метод) [24], оценивающий пространственные корреляции пикселей.

Для эксперимента были выбраны 15 тестовых контейнеров из [22, 23], в которые производилось встраивание случайных битовых последовательностей из расчёта 100 % их заполнения скрытыми данными. Рассматривались две реализации заполненных контейнеров, соответствующих двум вариантами значения амплитуды деформации ∆ = 1 , ∆ = 2 . Прочие параметры алгоритма скрытия: размер блока – 8×8, Гауссова RBF-функция, τ = 30 . В результате статистического стегоанализа тридцати полученных заполненных контейнеров критерий хи-квадрат и RS-метод не выявили присутствие скрытой информации. Для заполненных контейнеров эмпирические значения статистики хи-квадрат во всех случаях значительно превосходили теоретические для соответствующего числа степеней свободы и уровня значимости, что ошибочно подтверждает гипотезу об отсутствии ССИ. Для всех тестовых заполненных контейнеров в RS-методе вычисленные значения количества регулярных и сингулярных групп для отрицательной ( R_-M , S_-M ) и неотрицательной ( R_M , S_M ) маски отличались незначительно R _{- M} ≈ R_M , S _{- M} ≈ S_M (примерно соответствовали значениям, вычисленным для незаполненных контейнеров), т.о. ошибочно подтверждая гипотезу о незаполненности.

На основании полученных результатов можно сделать вывод о том, что предложенный алгоритм ССИ является устойчивым к широко распространённым статистическим стегоаналитическим критериям, однако следует ожидать, что в перспективе можно будет предложить критерий, выявляющий нарушение корреляции цветовых компонент при определённых амплитудах деформации.

Заключение

Тестирование стегоалгоритма на разных изображениях показало, что практическая его применимость в значительной мере определяется типами и характером содержимого используемых графических контейнеров. Наилучшие результаты фиксируются для естественных полноцветных фотографических изображений. Подобные изображения в общем случае предполагают отсутствие искусственных влияний и артефактов, нарушающих линейную зависимость цветовых компонент в малых локальных областях. Безусловно, естественные шумы, например, вносимые матрицей фотоаппарата, будут иметь место, но, как показали эксперименты, принципиального влияния на качество алгоритма они не оказывают. Следует отметить, что реализация стеганографического скрытия в изображения векторной графики и прочие синтетические изображе- ния (с нарушенной корреляцией цветовых каналов) в рамках предложенного подхода нецелесообразно.

С учётом проведённых предварительных экспериментов по исследованию устойчивости скрытой информации предлагаемый стегоалгоритм можно условно отнести к классу полухрупких. Необходимо также отметить обеспечиваемую за счёт нестандартной (не аддитивной или мультипликативной) природы стеганографического скрывающего преобразования устойчивость к специализированным статистическим стеганографическим атакам.

В качестве прочих достоинств предложенного в статье стегоалгоритма можно отметить сравнительно невысокую сложность процедур внедрения и детектирования, адаптируемость алгоритма под изображения-носители разного характера, возможность гибкой настройки параметров для уменьшения визуальной заметности результатов скрытия или повышения устойчивости встроенных данных к возможным трансформациям контейнера. К возможным недостаткам предложенного алгоритма следует отнести трудоёмкость процедуры предварительного обучения восстанавливающей информацию нейронной сети, невозможность корректной работы с некоторыми классами изображений (с явно невыраженной корреляцией цветовых компонент), а также неустойчивость скрытой информации к отдельным преобразованиям контейнера.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 13-0197507 р_центр_а.