Алгоритм траекторного управления беспилотным летательным аппаратом и антенной его радиолокационной станции при формировании радиолокационного изображения наземного объекта

Одним из актуальных направлений развития современной радиолокации в целях формирования высокоточных радиолокационных изображений наземных объектов на основе комплексной и интеллектуальной обработки потоков радиолокационных кадров является применение метода синтезирования апертуры антенны. Размещение радиолокационных станций (РЛС), реализующих такой метод на беспилотных летательных аппаратах (БПЛА), рационально с точки зрения экономических и эксплуатационных требований, однако накладывает ряд ограничений на условия их применения. Так, одним из наиболее существенных ограничений является нежелательное отклонение от номинальной траектории полета БПЛА, которое может привести к расфокусировке, геометрическим искажениям или фазовым ошибкам при формировании отдельных радиолокационных кадров [1]. Режим телескопического наблюдения позволяет устранить в некоторой степени требования к точности траектории полета БПЛА, однако требует отдельного управления антенной РЛС, размещаемой на борту летательного аппарата.

Отсюда возникает необходимость разработки обобщенного алгоритма управления с точки зрения построения траектории беспилотным летательным аппаратом и углом отклонения строительной оси антенны его бортовой РЛС, который позволит обеспечить требуемую траекторию полета БПЛА, наиболее благоприятную для наблюдения за наземными целями (НЦ), обеспечивающую комплексную и интеллектуальную обработку потоков радиолокационных кадров требуемого качества, в том числе получаемую с пространственно-распределенных РЛС, размещенных на двух и более БПЛА, функционирующих в группе.

Цель статьи – разработать алгоритм траекторного управления БПЛА и углом отклонения строительной оси антенны его малогабаритной бортовой РЛС, позволяющий обеспечить устойчивое наблюдение НЦ в интересах формирования радиолокационных видеокадров требуемого разрешения, пригодных для их комплексной и интеллектуальной потоковой обработки требуемого качества.

Рамки исследований

Исследования проводятся при следующих ограничениях.

• 1.    Наземная цель, подвижная или неподвижная.

• 2.    Рассматривается БПЛА самолетного типа, выполняющий полет с постоянной скоростью.

• 3.    Такие параметры, как угол поворота антенны бортовой РЛС и высота полета БПЛА, не должны превышать значений, обусловленных допустимыми перегрузками БПЛА.

• 4.    Радиус искривления траектории полета БПЛА обеспечивает его поперечное ускорение не более 5g.

• 5.    Время окончания наблюдения НЦ соответствует моменту, когда дальнейшее управление приведет к столкновению БПЛА с НЦ либо земной поверхностью.

• 6.    При синтезе алгоритма управления принято допущение, что каналы управления в вертикальной и горизонтальной плоскости работают независимо [2, 3], и так как БПЛА относительно наземной цели движется горизонтально, ограничен только в вертикальной плоскости, то и при решении задачи синтеза целесообразно рассматривать только вертикальную плоскость.

Постановка задачи синтеза алгоритма

В общем случае задача синтеза алгоритма оптимального управления летательным аппаратом в рамках статистической теории оптимального управления в пространстве состояний формулируется следующим образом [2, 4]: для системы с заданной частью xy W = Fy Wxy W+By Wu W + ^ (0 ’                           (1)

предназначенной для отработки процесса xT (?) = FT (/)xT (?) + 2, (?),                                                         (2)

при наличии измерений

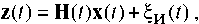
найти закон управления

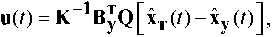
оптимальный по минимуму локального функционала качества

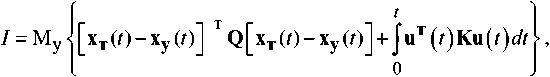
где F у ( t ) – динамическая матрица, учитывающая внутренние связи координат состояния процесса (1); x _у( t ) – n-мерный вектор управляемых фазовых координат; B _у( t ) – матрица эффективности управления; u ( t ) – r-мерный вектор сигналов управления (r≤n); ξ х ( t ) – n-мерный вектор центрированных гауссовских возмущений процесса x _у( t ) с известной матрицей G _y односторонних спектральных плотностей; F т ( t ) – динамическая матрица, учитывающая внутренние связи координат состояния процесса (2); x _т( t ) – n-мерный вектор требуемых фазовых координат; ξ_т( t ) – n-мерный вектор центрированных гауссовских возмущений процесса x т ( t ) с известной матрицей G т односторонних спектральных плотностей; H ( t ) – матрица связи обобщенного вектора состояния x = |\t Xy с m-мерным вектором z наблюдений (измерений) ( m ≤ 2 n ); ξ и ( t ) – n-мерный вектор центрированных гауссовских шумов измерений с известной матрицей G _и односторонних спектральных плотностей; К – матрица штрафов за величину сигналов управления; Q – матрица штрафов за точность управления [x_T(7)-x_y(o]; М_{у –} математическое ожидание при условии, что имеются результаты измерения хотя бы части фазовых координат x у и x т .

Для линейно-квадратично-гауссовской задачи синтеза, требованиями для которой являются линейность моделей, квадратичность функционалов и гауссовость шумов, условия упро- щения синтеза оптимальной РЭСУ определяются фундаментальной теоремой разделения (статистической эквивалентности), заключающейся в следующем.

Для линейных моделей (1) и (3) в условиях гауссовских возмущений ξ_х и ξ_и при оптимизации системы по квадратичному функционалу качества (5) алгоритмы оценивания и алгоритмы управления можно синтезировать раздельно (независимо). При этом алгоритм функционирования статистического регулятора, учитывающего влияние возмущений ξ х и ξ_и, будет аналогичен (статистически эквивалентен) алгоритму функционирования детерминированного регулятора, полученному для ситуации, когда ξ х =0 и ξ и =0, при условии замены в последнем координат состояния x и параметров системы F , B , и H их оптимальными оценками X,F,В, ии. Наилучшим по критерию минимума среднеквадратической ошибки [2–4] приближением оценки X к случайному процессу х является условное математическое ожидание

Х=Лф1г}.                                               (6)

Оценивание вектора х будет тем точнее, чем точнее сведения о параметрах используемых процессов и систем. В моделях (2) роль параметров играют коэффициенты матриц F т , G т , F у , B _у, G _у, H , G _и. Для текущего оценивания параметров целесообразно использовать алгоритмы теории оптимальной идентификации, которые позволяют найти оценки, оптимальные по критерию минимума среднеквадратической ошибки

H = W{H|Z}, F = ^{F|z}, B = W{B|Z},G = M'G|Z;,               (7)

используемые в алгоритмах фильтрации и вычисления сигналов управления.

Для использования (4) необходимо иметь модели состояния и измерений, которые должны обеспечивать решение следующих задач [2–4]:

учет основных кинематических связей оптимизируемой системы;

выполнение условий управляемости и наблюдаемости [2–4] при использовании стандартных рулевых органов и типовых измерителей;

формирование на борту БПЛА значений требуемого поперечного ускорения j т .

Динамическая модель взаимного перемещения БПЛА и НЦ

Динамика взаимного перемещения БПЛА относительно НЦ с учетом угла отклонения строительной оси антенны представлена на рис. 1, а также на рис. 2 изображено более подробно положение антенны относительно строительной оси БПЛА во время полета.

На рис. 1 и 2 также обозначено:

D – расстояние между БПЛА и НЦ; V _бпла – текущая скорость БПЛА; V _{нц –} скорость перемещения НЦ; ω – угловая скорость вращения линии визирования между БПЛА и НЦ; φ бпла – текущее значение бортового пеленга НЦ с БПЛА; φ_тр – требуемое значение бортового пеленга НЦ с БПЛА; α А – угол отклонения строительной оси антенны; α А тр – требуемый угол отклонения строительной оси антенны; ε – угол отклонения линии визирования; ψ_бпла – текущее значение курса полета БПЛА; ( x нц, y нц ) – координаты НЦ; ( x ла, у ла ) – координаты БПЛА.

Исходя из анализа требуемой траектории наведения БПЛА она может быть разбита на три этапа (рис. 3).

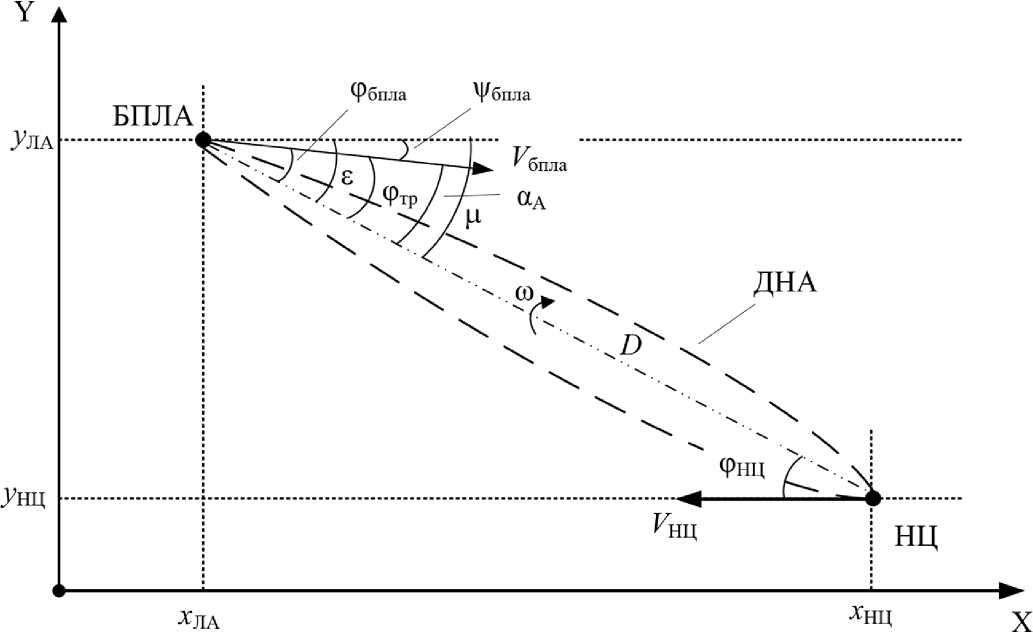
Рис. 1. Взаимное расположение БПЛА и НЦ (в вертикальной плоскости)

Fig. 1. The relative position of the UAV and the ground object (in the vertical plane)

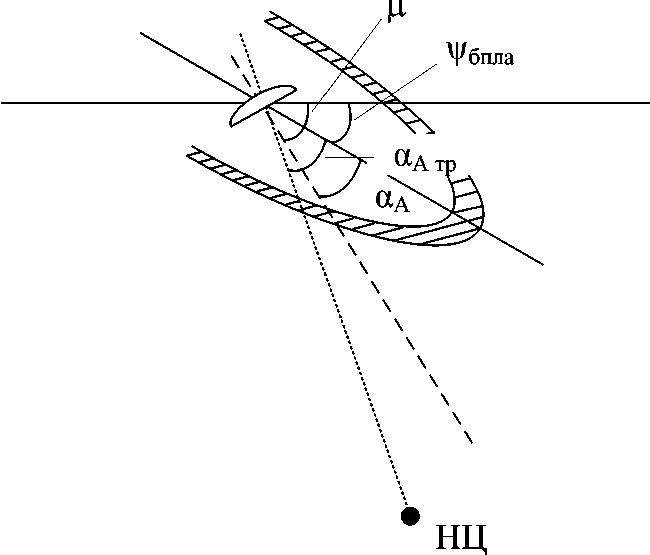
Рис. 2. Положение антенны относительно строительной оси БПЛА в процессе сопровождения НЦ

Fig. 2. The position of the antenna relative to the UAV’s construction axis during ground object tracking

На первом этапе сопровождения управление осуществляется углом отклонения строительной оси антенны бортовой РЛС, траектория полета БПЛА не изменяется до тех пор (горизонтальный полет), пока угол отклонения строительной оси антенны α А не будет равен максимальному углу отклонения α А max , а поперечное ускорение БПЛА j бпла не превысит допустимого значения j бпла доп (допустимое значение ускорения j бпла доп рассчитывается при максимально возможном значении скорости БПЛА).

Максимальный потребный угол отклонения строительной оси антенны определяется формулой [5]

α A max

φ бпла т max

– Δα,

где φбпла т max – максимальное допустимое значение угла пеленга при сопровождении НЦ в бортовой РЛС БПЛА; Δα – запас по углу поворота строительной оси антенны, необходимый для исключения потери НЦ при динамических бросках БПЛА на траектории, в том числе вызванных турбулентностью атмосферы.

На первом этапе алгоритм управления можно представить как ΔA = αА тр – αА.

Для упрощения математических выкладок в дальнейшем собственная скорость НЦ при управлении отклонением строительной оси антенны бортовой РЛС не учитывается. Собственная скорость НЦ будет учитываться при управлении поперечным ускорением БПЛА.

Известно [6], что при значительных углах поворота строительной оси антенны необходимо учитывать ошибки обтекателя, которые обусловлены несовершенством его конструкции и проявляются в дополнительном непредсказуемом смещении равносигнального направления относительно линии визирования.

За счет электрических неоднородностей в обтекателе нулевое напряжение на выходе пеленгационного устройства угломера устанавливается при смещении строительной оси антенны бортовой РЛС БПЛА на угол Δφ = ± k _обα_А относительно направления строительной оси антенны на НЦ, где k об – крутизна пеленгационной характеристики обтекателя.

На втором этапе, когда угол отклонения строительной оси антенны α_А равен максимальному потребному углу α_{А max}, либо дальность D до НЦ близка значению, на котором требуемое поперечное ускорение БПЛА j бпла тр в дальнейшем превысит допустимые значения j бпла _доп, управление осуществляется перегрузкой при фиксированном, близком к максимальному потребному значению угла отклонения строительной оси антенны (α_{А max}), до момента, при котором значение курса ракеты будет соответствовать значению ψ_бпла = 90° – α_{А max}, означающее вертикальное облучение НЦ (сверху вниз). Дальнейшее управление поперечным ускорением

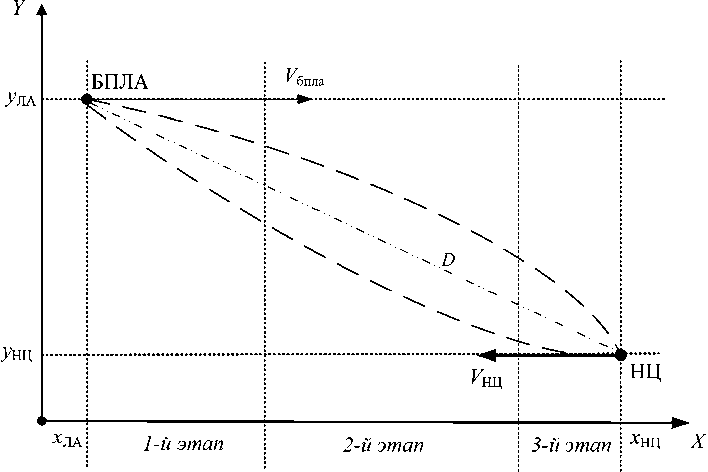
Рис. 3. Этапы сопровождения НЦ в бортовой РЛС БПЛА

Fig. 3. The stages of tracking a ground object in an on-board UAV radar station

при фиксированном максимальном угле отклонения строительной оси антенны приведет к неоправданному искривлению траектории полета УР, что, в свою очередь, скажется на увеличении дальности полета БПЛА и времени наблюдения НЦ.

На втором этапе алгоритм может быть представлен известными ранее алгоритмами, широко представленными в [2–4], например алгоритмом Δj = j _т – j .

На третьем этапе наведения должно осуществляться управление углом отклонения строительной оси антенны и поперечным ускорением БПЛА одновременно, что требует решения задачи синтеза алгоритма совместного траекторного управления поперечным ускорением БПЛА и углом отклонения строительной оси антенны бортовой РЛС.

Условия синтеза оптимального алгоритма

При получении уравнений состояния предполагается, что выполняются следующие допущения:

• -    при самонаведении на борту БПЛА формируются значения требуемого поперечного ускорения;

• -    БПЛА и НЦ могут маневрировать с поперечными к линии визирования «БПЛА-НЦ» ускорениями j _бпла и j _нц соответственно, а ускоряться – с продольным к линии визирования «БПЛА-НЦ» ускорением j прод нц.

Для линейных моделей (1) и (3) в условиях гауссовских возмущений ξх и ξи при оптимизации системы по квадратичному функционалу качества (5) алгоритмы оценивания фазовых координат вектора состояния и алгоритмы траекторного управления можно синтезировать раздельно (независимо) [2–4].

Рассмотрим более подробно динамику взаимного перемещения БПЛА и НЦ, представленную на рис. 1 с учетом рис. 2.

Введем угол

Ц = E - фбпла + ССд.                                                         (8)

Если продифференцировать выражение (8), получим ц = £ - Фбпла + осд , или ц — га — Фбпла + осд , где ω = 8.

Тогда представим угловую скорость ЛВ как

(В — Ц — ОС а + Фбпла ■                                                        (9)

Тогда с учетом побочных явлений угломера, рассмотренных ранее, угловая скорость линии визирования будет иметь вид

(В = Ц - ОС а + Фбпла — ^обУбпла ■                                        (10)

При управлении отклонением строительной оси антенны динамическая модель, описывающая данный процесс, будет иметь вид [3]

«а=®а;          а_А(О) = а_АО;

“A =-®a+-ua+^a; юа(О) = юао, где b – коэффициент усиления привода поворота антенны; T – постоянная времени.

Проецируя скорости V бпла и V нц на линию визирования и нормаль к ней, получаем

В _ 1нцС05Фнц ^бпла^^бпла =	(12)
^® = Фбпла sin Фбпла - Фщ s*n Фнц •	(13)

Скорость полета БПЛА самолетного типа примерно в том же скоростном диапазоне, что и скорость подвижных наземных объектов – автомобилей, поездов, и т.п., следовательно, необходимо их учитывать.

Для упрощения выкладок примем допущение, что косинусы всех углов примерно равны единице, а синусы – своим аргументам.

Дифференцируя выражение (13) по времени при V бпла = const, получаем

D(B + Deb = ^бплаФбпла -ФцФнц - ФцФнц                          (14)

или

^®_^бплаФ Фбпла) ФщФнц ^ц^ Фнц)

Раскрывая скобки, и с учетом того, что £ И, Фбпла Фбпла /бпла, ФщФнц /прод нц и 1 нц Фнц = /нц получим

. 1бпла 1вд В со =----------------со-

D

р (/бпла /нц + /проднц) ■

Так как 1щ 1бпла ^_ В , а ^и- Н ^Л + Фбпла ± ^обФбпла, тогда в конечном виде выражение (13) можно представить как

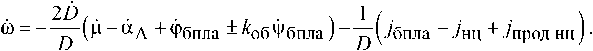
Для определения изменения бортового пеленга НЦ с БПЛА в процессе наведения представим формулу (12) как

Фбпла = arcsin

Рю + Рнц^Фнц

1'бпла

Дифференцируя (17) по времени при V _бпла = const, получаем

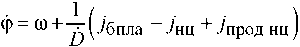
или с учетом выражения (10)

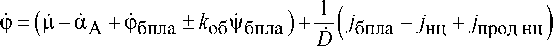
Таким образом, на основании рис. 1 и выражений (16) и (19) динамическая модель, описывающая взаимное перемещение БПЛА и НЦ, будет иметь вид

Фбпла (и “А + Фбпла ± ^об^бпла ) + ^ (^бпла Лщ + 7прод нц ) + ^

Фбпла (0) = Фбпла 0’

'Фбпла ’

Ш = -

р (^ ^А + Фбпла ±^o6Vбила) рубила 7нц +/прод нц ) + ^го ’

'ГО ’

ю(0) = ®Q.

^бпланц’

‘ ^бпланц /ирод ’

W) = Ab

^бпла нц (0)_^бпланцО ’

/ирод “/ирод +^/прод ’ -/прод (°) /продО’ где В — /бпланц – скорость изменения расстояния между БПЛА и НЦ; α – коэффициент, характеризующий маневренные свойства БПЛА.

Адекватность динамической модели (20), (21) проверялась путем сравнения с результатами созданных ранее и хорошо себя зарекомендовавших моделей, представленных в [2–4], неадекватность составила не более 11 %.

Условие наблюдаемости [2–4] системы (20), (21) измерениями выполняется, поскольку в каждой группе функционально связанных координат модели состояния измеряются как минимум нулевые производные.

Данная динамическая модель взаимного перемещения БПЛА и НЦ в процессе наведения показывает динамику изменения основных параметров во времени.

Синтез алгоритма

Для синтеза управления необходимо иметь модели состояния (1), (2) и функционал качества в виде (4) [2–4].

Исходя из того что параметрами управления являются угол отклонения строительной оси антенны бортовой РЛС и поперечное ускорение БПЛА, при синтезе оптимального алгоритма управления вектор управления будет иметь вид

U =

Да

о

0А,-

аА тр аА 0

./била — 7нц + ./ирод нц

Требуемыми параметрами для системы самонаведения БПЛА, учитывающими управле- ние отклонением строительной оси антенны, угловой скоростью поворота антенны, ракурсом радиолокационного наблюдения в АРГС ракеты отраженных от НЦ сигналов и угловой ско- ростью вращения линии визирования «БПЛА-НЦ» являются αА тр, ωА тр, φбпла тр и ωтр соответственно, т.е. вектор требуемых координат состояния хт будет иметь вид аА тр

®А тр

^бпла тр -Фа ®тр ^_®А

Управляемыми параметрами для системы самонаведения БПЛА являются αА, ωА, φбпла и ω, следовательно, вектор управляемых координат состояния xу будет следующим аА

X

®А

Фбпла го

Так как параметрами управления являются угол отклонения строительной оси антенны α А и боковое ускорение БПЛА j бпла , а управляемыми параметрами – α А , ω А , φ бпла и ω, то матрицу эффективности сигналов управления В у образуют коэффициенты при векторе управления u в динамических моделях (11) и (20)

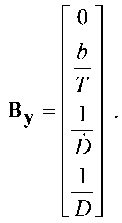
Матрицы штрафов за точность наведения Q и величину сигналов управления K в формуле (4) с учетом размерности матриц (22)–(25) имеют вид

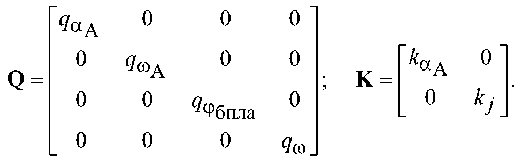
В результате функционал качества (5) принимает вид аА тр — аА

® А тр - ® А Фбпла тр — аА “Фбпла юТр — (Од — а>

^«А О

о

о

I OL

аА тр аА О

о

о

о

о

^А О

о

о

о

^Фбпла О

о

?(oj _

аА тр “ аА

® А тр - ® А Фбпла тр “ аА “ Фбпла юТр — Юд — со

./била ./нц + ./прод нц _

^А О

о

к;

аА тр аА О

о

./бпла ./нц + ./прод нц _

dt

Подставив выражения (22) – (25) в выражение (4), получим следующее соотношение аА тр аА О

О

,/бпла 7нц + ,/прод нц _

^ад О

О Ад

1-1

о ь_ т

I

_D_

9«А

О

О

О

О

^®А о

о

О

о

^Фбпла О

О

о

О

а А тр — аА

® А тр _ ® А Фбпла тр — а А — Фбпла СОТр — (Од — (О

или

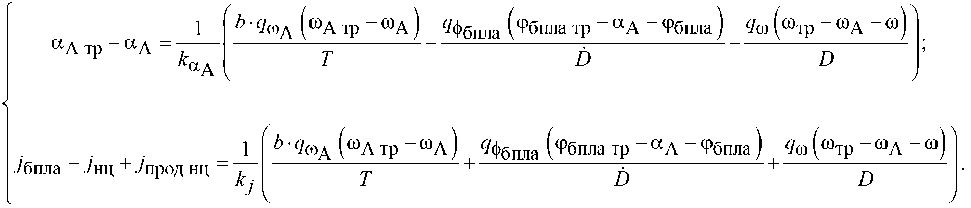
Выполнение при синтезе условий линейно-квадратично-гауссовской задачи [2–4] позволяет заменить истинные значения координат состояния векторов х _т и х _у их оптимальными оценками, тогда алгоритм траекторного управления имеет вид

ГАд ;

Л= Л (28)

где ^ДА ^а А тр “А – параметр рассогласования, определяющий несоответствие текущего α_А и требуемого α_{А тр} значений угла отклонения строительной оси антенны; ^Д/ ^— Убила т Убила – параметр рассогласования, определяющий несоответствие текущего j б _пла и требуемого j б _{пла т} значений поперечного ускорения БПЛА.

Требуемые значения угла отклонения строительной оси антенны и поперечного ускорения БПЛА определяются выражениями соответственно

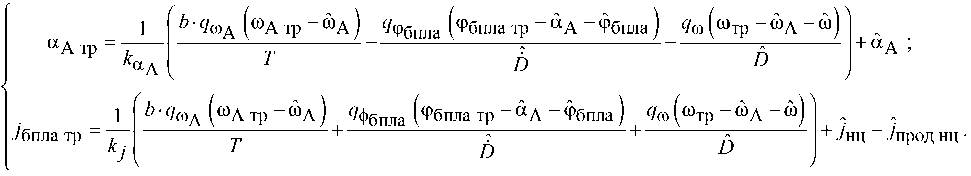
Анализ полученных моделей состояния, а также сравнительный анализ полученных алгоритмов с алгоритмами наведения, представленными в [2–4], позволяет сделать следующий вывод : применение синтезированного алгоритма одновременного управления лучом антенны и поперечным ускорением БПЛА – носителя РЛС позволит обеспечить траекторию полета БПЛА, наиболее благоприятную для радиолокационного наблюдения за наземной целью.

Для формирования сигналов управления в соответствии с алгоритмом (28) необходимо иметь оценки следующих координат:

• -    дальность D от БПЛА до НЦ;

• -    пеленг φ НЦ с БПЛА;

• -    курс БПЛА ψ бпла ;

• -    угловая скорость ω вращения линии визирования НЦ с БПЛА;

• -    скорость V _нц наземной цели;

• -    поперечное j нц и продольное j прод нц ускорения НЦ;

• -    угол отклонения строительной оси антенны α_А;

• -    угловая скорость поворота строительной оси антенны ω_А.

Синтезированный алгоритм управления (28) является всевысотным и всеракурсным, обеспечивая устойчивое наблюдение за наземным объектом.

Всевысотность обеспечивается использованием в качестве сигнала управления поперечного ускорения, а не углов отклонения рулей, эффективность которых зависит от высоты. Все-ракурсность обеспечивается учетом в законе управления знака и величины ω.

Таким образом, синтезированный алгоритм управления (28) является нестационарным, так как коэффициенты передачи учитываемых фазовых координат, определяющие их значимость в формировании результирующего сигнала управления, автоматически адаптируются к условиям наблюдения в зависимости от характера НЦ (подвижная, неподвижная, с ускоре-нием/торможением, и т.п.), осуществляется автоматическое перераспределение приоритетов управления от устранения угловых ошибок на начальном участке к устранению ошибок по точности сопровождения («промахов») на конечном, что позволяет обеспечить наилучшее по точности и экономичности управление БПЛА и реализовать оптимальное по минимуму локального функционала качества управление БПЛА – носителем РЛС при наблюдении за наземной целью.

Техническая реализация алгоритма

На рис. 4 представлена функциональная схема, поясняющая техническую реализацию синтезированного алгоритма, а на рис. 5 – этапы, поясняющие процесс наблюдения [7, 8].

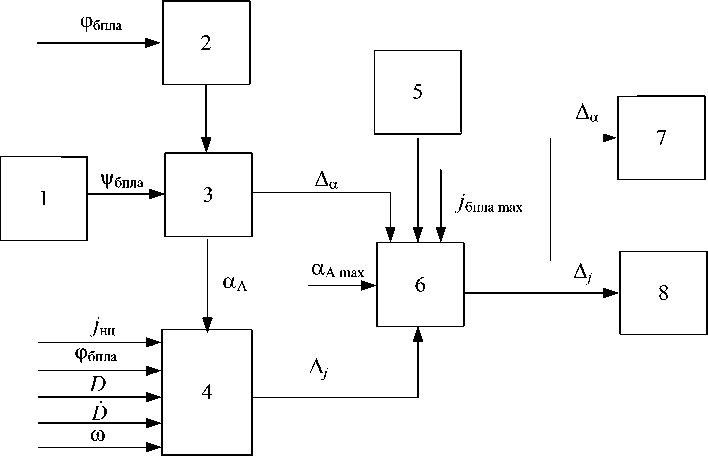
Рис. 4. Функциональная схема, поясняющая способ наблюдения НЦ: (1 – блок автономных датчиков БПЛА, 2 – блок расчета статической пеленгационной характеристики обтекателя БРЛС Δφоб, 3 – блок формирования сигнала управления отклонением строительной оси антенны, 4 – блок формирования сигнала управления поперечным ускорением БПЛА, 5 – блок расчета поперечного ускорения БПЛА, 6 – анализатор, 7 – привод антенны, 8 – привод рулей БПЛА)

Fig. 4. Functional diagram explaining the method of observing a ground object: (1 – the unit of autonomous UAV sensors, 2 – the unit for calculating the static direction finding characteristics of the radar fairing Δφоб, 3 – signal generation unit for controlling the deviation of the antenna construction axis, 4 – the UAV lateral acceleration control signal generation unit, 5 – the UAV lateral acceleration calculation unit, 6 – the analyzer, 7 – antenna drive, 8 – UAV steering ωheel drive)

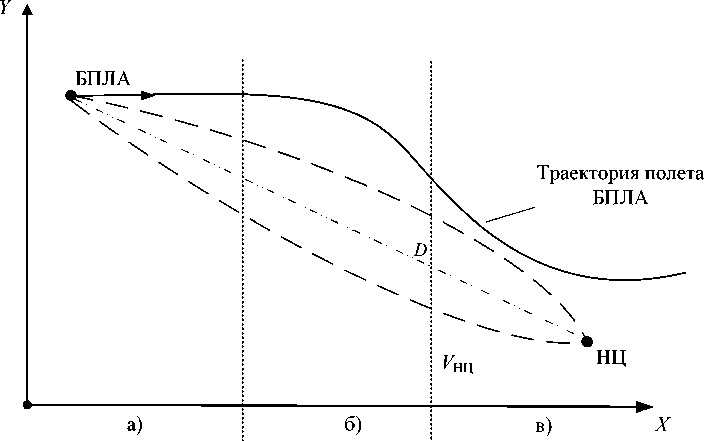
Рис. 5. Этапы сопровождения НЦ в РЛС БПЛА

Fig. 5. The stages of tracking a ground object in an on-board UAV radar station

С блока формирования сигнала управления отклонением строительной оси антенны (рис. 4) на первый вход анализатора поступает сигнал рассогласования Δ_α, определяющий несоответствие требуемого и текущего углов отклонения строительной оси антенны в вертикальной плоскости, формируемый с учетом статической пеленгационной характеристики обтекателя Δφ об , рассчитываемой в блоке расчета статической пеленгационной характеристики обтекателя БПЛА от угла пеленга. Одновременно на второй вход анализатора с выхода блока формирования сигнала управления поперечным ускорением БПЛА в вертикальной плоскости поступает сигнал Δ j управления БПЛА в вертикальной плоскости, формируемым в соответствии с (28). На третий вход анализатора с выхода блока расчета поперечного ускорения БПЛА в вертикальной плоскости поступает текущее значение поперечного ускорения БПЛА в вертикальной плоскости.

На первом выходе анализатора формируется сигнал Δ α отклонения строительной оси антенны в вертикальной плоскости, поступающий на привод антенны, а сигнал Δ j управления поперечным ускорением БПЛА на втором выходе анализатора не формируется, что обеспечивает прямолинейную траекторию полета БПЛА (рис. 5 а ).

При достижении угла отклонения строительной оси антенны заданного, близкого к максимальному значения, или рассчитываемое в блоке расчета поперечного ускорения БПЛА в вертикальной плоскости (рис. 4) будет максимально допустимым, на втором выходе анализатора формируется сигнал Δ j управления поперечным ускорением БПЛА в вертикальной плоскости, формируемым в соответствии с (28), который подается на привод рулей БПЛА, а сигнал Δ α отклонением строительной оси антенны на первом выходе анализатора не формируется, что обеспечивает криволинейную траекторию полета БПЛА в вертикальной плоскости (рис. 5 б ).

При достижении угла полета БПЛА в вертикальной плоскости относительно НЦ значения ψбпла = 90° – αА max, на первом и втором выходах анализатора (рис. 4) одновременно формируются сигнал управления Δα отклонением строительной оси антенны, поступающий на привод антенны, возвращающий антенну в нулевое положение относительно строительной оси БПЛА, а также сигнал Δj управления поперечным ускорением БПЛА в вертикальной плоскости, поступающий на привод рулей БПЛА (рис. 5в), обеспечивая прямолинейную траекторию его полета.

Предложенный способ позволит технически реализовать синтезированный алгоритм управления БПЛА и антенным лучом его бортовой РЛС при наблюдении за НЦ. Ключевыми отличиями способа являются следующие:

во-первых, на начальном этапе полета БПЛА после момента обнаружения НЦ формирование сигнала отклонения строительной оси антенны бортовой РЛС осуществляется с учетом статической пеленгационной характеристики обтекателя БПЛА, поступающего на привод антенны при отсутствующем сигнале управления поперечным ускорением БПЛА в вертикальной плоскости, обеспечивая прямолинейную траекторию его полета;

во-вторых, на следующем этапе полета БПЛА осуществляется формирование сигнала управления его поперечным ускорением в вертикальной плоскости, поступающего на привод рулей при отсутствующем сигнале управления отклонением строительной оси антенны, что позволяет обеспечить криволинейную траекторию полета в вертикальной плоскости при постоянном максимальном угле отклонения строительной оси антенны;

в-третьих, на заключительном этапе осуществляется параллельное формирование сигнала управления отклонением строительной оси антенны, возвращающего её в нулевое положение относительно строительной оси БПЛА, и сигнала управления поперечным ускорением БПЛА в вертикальной плоскости, поступающего на привод его рулей, обеспечивая прямолинейную траекторию полета.

Вывод

Таким образом, синтезированный алгоритм траекторного управления БПЛА и углом отклонения строительной оси антенны его малогабаритной бортовой РЛС позволяет обеспечить устойчивое наблюдение НЦ в интересах формирования радиолокационных видеокадров требуемого разрешения, пригодных для их комплексной и интеллектуальной потоковой обработки требуемого качества.

В дальнейшем реализация разработанного алгоритма на двух и более БПЛА, функционирующих в группе, позволит обеспечить формирование радиолокационных видеокадров передней зоны обзора в пространственно-распределенной системе малогабаритных бортовых РЛС [1]. Определение требований к взаимному расположению носителей малогабаритных бортовых РЛС, объединенных в группу, выполняющих полетное задание и формирующих радиолокационные видеокадры для передней зоны обзора позволит решить комплексную проблему. Эта проблема требует междисциплинарного подхода, связана, с одной стороны, с обеспечением точности заданной траектории полетов носителей малогабаритных БРЛС и их антенн, с другой – с формированием радиолокационных видеокадров в передней зоны обзора, формируемых в пространственно-распределенной системе малогабаритных БРЛС.