Алгоритм трансляции модели бизнес-процессов в модель GERT-сети

Повышение эффективности деятельности организации связано с совершенствованием бизнес-процессов. Для этого современная управленческая наука использует моделирование и анализ бизнес-процессов с целью обнаружения «узких мест», оценки структуры и показателей бизнес-процессов и т.п. Для моделирования и анализа бизнес-процессов используются различные подходы и средства. В первую очередь следует отметить методологии описания бизнес-процессов IDEF, ARIS, BPM. Поддерживающие данные методологии программные средства – AllFusion Process Modeler (BPWin), ARIS Platform позволяют как осуществлять формальное описание моделей деятельности, так и производить оценку числовых параметров процессов – времени выполнения процесса, стоимости процесса и т.п. Решение данной задачи достигается как непосредственно (например, расчет стоимости процессов с использованием методики функционально-стоимостного анализа в BPWin), так и с использованием подключаемых программных модулей или модулей расширения (BPArena, ARIS Simulation). Для анализа числовых параметров бизнес-процессов могут применяться и непосредственно программные продукты для имитационного моделирования – AnyLogic, GPSS и др. Также при моделировании и анализе бизнес-процессов используется аппарат сетей Петри [1, 2], аппарат цепей Маркова и др.

Однако при анализе числовых показателей бизнес-процессов аналитики неизбежно сталкиваются с дилеммой: либо обеднение функциональности анализа путем исследования лишь детерминированных показателей времени и стоимости процесса, либо получение вероятностных данных процесса. При этом ценой приемлемой точности в имитационном эксперименте является очень высокая трудоемкость решения [3].

Таким образом, авторы ставят перед собой цель разработать модели и алгоритмы, позволяющие прогнозировать числовые параметры бизнес-процесса, а именно время выполнения, движение материальных ресурсов (включая деньги) и загрузку трудовых ресурсов, при условии более высокой точности и более низкой трудоемкости, чем это позволяет сделать имитационный эксперимент.

Авторы предположили, что данная задача может быть решена применением для числовой оценки бизнес-процессов аппарата GERT-сетей (GERT - graphical evaluation and review technique). Классическое описание GERT-сетей приведено в декларации Прицкера [6], на русском языке описание GERT-сетей можно найти в книге Филлипса и Гарсиа-Диаса [4].

Описание бизнес-процессов. Для описания бизнес-процессов в статье будет использоваться нотация ARIS eEPC. Она принадлежит к классу событийных моделей деятельности. По изобразительной мощности она примерно соответствует IDEF3 и UML State-Chart Diagram, обладая по сравнению с ними рядом преимуществ, главное из которых – большее количество символов модели, специально адаптированных для предметных областей, – офисные процессы, производственные процессы. В данной работе мы будем использовать подмножество модели eEPC, изображенное на рисунке 1.

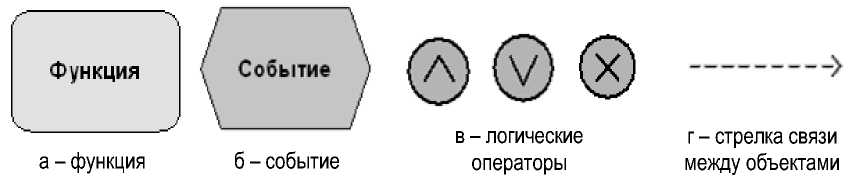
Рис. 1. Объекты модели ARIS eEPC

Для решения задачи трансформации модели eEPC в GERT-сеть опишем обе модели в графовом виде, а затем произведем сопоставление графов.

Модель в нотации ARIS eEPC может быть описана графом D

D = ( S о, L о), где S0 = {s 1, ..., sq} - множество символов модели eEPC (процессы, события, перекрестки); q - количество символов; L0 = {l 1, ..., la} - множество связей (дуг) модели eEPC; a - количество дуг; V li е L0, соединяющая объекты модели eEPC, характеризуется атрибутом pli – вероятность выполнения дуги li ;

F о =|| f L|| - a * q матрица; F ₀ ^S =|| f j|| - q x a матрица; f j - инцидентность l i c S j (связей с символами); f_j^S_i – инцидентность s_j с l_i (символов со связями).

X о ^{е S} о , B о ^{е S} о , R о ^{е S} о , где X _о = { x 1 , ..., x u } - множество объектов типа «событие»;

• u – количество событий;

• B ₀ = { b 1 , ..., b m } - множество объектов типа «функция»;

• \ m – количество функций; каждая функция характеризуется рядом атрибутов, значимым из которых является t_bm – время работы функции b_m .

Кроме времени, для функции могут быть заданы другие параметры работы (стоимость, количество необходимых ресурсов и т.п.).

R _о = { r 1 , ..., r k } - множество объектов типа «правило» (AND, OR, XOR), задающих логику ветвле-ния/слияния бизнес-процесса; k – количество правил. Множество правил ветвления R ₀ состоит из элементов множества RAnd , ROr , RXor , где RAnd – множество правил ветвления типа AND (И); ROr – множество правил ветвления типа OR (ИЛИ); RXor – множество правил ветвления типа XOR (исключающее ИЛИ).

Модель GERT-сети. GERT-сети являются вариантом полумарковских моделей, но случайные величины в них характеризуется не только дисперсией, но и законом распределения. При использовании GERT-сетей, как правило, определяют значения переменных, связанных с первыми моментами распределения выходной величины относительно начала координат (математическое ожидание, дисперсию, коэффициенты асимметрии и эксцесса).

Математическая модель GERT-сети может быть описана направленным взвешенным графом G

G = (V, E), где V = {v1, ..., vh} - множество вершин (узлов); h - количество узлов; E = {e1, ..., ec} - множество направленных ребер (дуг); c – количество дуг; Rs – множество источников (начальная вершина графа), такое, что Rs е V; Src - множество стоков (конечная вершина графа), такое, что Src е V.

Связность узлов и дуг GERT-сети определим при помощи двух матриц инцидентности. Определим F^ = || f iE || - c x h - матрицу инцидентности дуг с узлами, соответственно f j - инцидентность дуги e i c узлом V j . Матрица F V =|| f /E|| - h x c определяет инцидентность узлов с дугами, соответственно f V -инцидентность узла v_j с дугой e_i .

Узлы GERT-сети интерпретируются как состояния системы, а дуги как переходы из одного состояния в другое. Такие переходы связываются с выполнением обобщенных операций, характеризуемых плотностью распределения и вероятностью выполнения.

Направленное ребро (дуга) ассоциируется с тем, из какого узла i оно выходит и в какой узел j входит, и обозначается как дуга <  i , j > . Дуга <  i , j >  в рамках GERT-сетей рассматривается как «работа на дуге» и имеет вес некоторого аддитивного параметра (например, время выполнения работы). Для GERT-сети весом дуги <  i , j >  является вектор [ p ij , F ij ] , где p ij - условная вероятность выполнения дуги <  i , j >  при условии активации узла i , а F ij - условная функция распределения времени выполнения дуги <  i , j >  , при условии, что <  i , j >  выполняется. При этом дуга <  i , j > , для которой F ij = 0 , называется «холостой» дугой или дугой, на которой работа не выполняется.

Следует отметить, что параметр F _ij может соответствовать не только времени (используется в данной работе) выполнения дуги, но и любой аддитивной величине, характеризующей выполнение процесса – например, стоимости, расходу материальных ресурсов и т.п. Кроме того, речь может идти о векторе аддитивных параметров.

Каждый узел сети имеет входную и выходную функции активации. Входная функция определяет условие, при котором узел может быть активирован. Выходная функция определяет совокупность условий, связанных с результатом активизации узла.

Виды входных функций: AND-функция – узел активируется, если выполнены все дуги, входящие в него; IOR-функция – узел активируется, если выполнена любая дуга или несколько дуг, входящих в него; EOR-функция – узел активируется, если выполнена любая дуга, входящая в него, при условии, что в данный момент времени может выполняться только одна дуга, входящая в данный узел.

Виды выходных функций: детерминированная функция (DT) – все дуги, выходящие из узла, выполняются, если узел активирован; стохастическая функция (ST) – только одна дуга, выходящая из узла, выполняется с заданной вероятностью, если узел активирован.

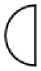
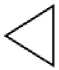
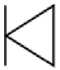
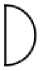
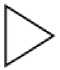
а – функция б – IOR

в – EOR

г – детерминирован-     д – стохастический ный выход              выход

Рис. 2. Входные и выходные функции узлов GERT-сети

Комбинируя все входные и выходные функции, получаем шесть различных типов узлов:

Рис. 3. Типы узлов GERT-сети

Узел с входной AND-функцией и стохастической выходной функцией называется STEOR-узел.

Активация узла означает, что система перешла в некоторое состояние и определяет множество дальнейших работ (операций). Одна или несколько работ (операций) начинают свое выполнение сразу после активации узла, являющегося их началом. Активация узла происходит, если его входная функция выполнена. После выполнения выходной функции активированного узла он становится неактивным.

Результаты функционирования графа G могут быть представлены в виде набора параметров выполняемой сети: вероятность активации стока сети, функция распределения стока и др.

Таким образом, GERT-сеть – это сеть с источниками Rs и стоками Src вида «работа на дуге», в которой каждый узел принадлежит одному из шести типов узлов, для каждой дуги <  i, j >  определен вес вида [ p ij , F ij ] с вышеуказанным значением и задано начальное распределение источников сети.

Алгоритм трансляции. При первоначальной формулировке алгоритма трансляции авторы столкнулись с очевидным противоречием графических нотаций EPC и GERT. Противоречие заключается в том, что в eEPC модели активным элементом, обозначающим действие, является процесс (узел), а в GERT – дуга. Чтобы преодолеть это противоречие, было решено сопоставлять с процессом eEPC не одиночную дугу

GERT-сети, а сочетание «узел+ребро». На уровне описаний бизнес-процессов это соответствовало связке «процесс+событие». Для целей исследования числовых параметров бизнес-процесса можно говорить, например, о том, что время выполнения дуги GERT-сети сопоставляется с временем наступления финального события процесса.

При таком подходе для трансляции модели бизнес-процесса из нотации ARIS eEPC в соответствующую GERT-сеть необходимо выполнить следующие действия.

Сопоставим каждому символу модели eEPC вершину (узел) GERT-сети. Для каждого элемента eEPC модели s i создается соответствующий ему узел GERT-сети v i , таким образом, q = h . На данном этапе каждый узел GERT-сети имеет EOR-функцию на входе и стохастическую функцию на выходе, тем самым мы сохраняем условие, что в каждый символ (объекты: событие, функция) модели eEPC входит только одна связь и только одна связь с p j = 1 выходит из объекта.

После выполнения этого сопоставления первоначальный вариант матрицы инцидентности GERT-сети может быть задан простым приравниванием матриц F 0 = F 0 и F V = F 0 .

Для V s j , S j е R ₀ и существует n связей l i , n >  1 , для которых f j = 1 , определим (возьмем) соответствующий ему узел V j и сопоставим V v j входную функцию по следующим принципам (табл. 1).

Преобразование операторов на слияние

Таблица 1

Оператор eEPC	Узел GERT-сети
S j е RAnd	vj с входной AND-функцией
s j е ROr	vj с входной IOR-функцией
s j е RXor	vj с входной EOR-функцией

Для правил из RAnd , ROr , RXor соответствующие узлы v_j имеют стохастическую функцию выхода.

Для V S j , S j u R ₀ и существует n связей l i , n >  1 , для которых f S = 1 , определим (возьмем) соответствующий ему узел V j и сопоставим V V j выходную функцию по следующим принципам (табл. 2).

Преобразование операторов на разветвление

Таблица 2

Оператор eEPC	Узел GERT-сети
s j е RAnd	vj с детерминированной выходной функцией DT
s j е ROr	Нет прямого решения в аппарате GERT, предлагаемое авторами решение будет рассмотрено в другой статье
s j е RXor	v j со стохастической выходной функцией ST

Для правил из RAnd , ROr , RXor соответствующие узлы v_j имеют EOR-функцию входа.

Определим вероятность выполнения дуг GERT-сети. Для V l i , для которой f S = 1 , возьмем соответствующую ей дугу e i е E и определим вектор [ P ji , F ji ] в соответствующей позиции f S = 1 матрицы F 0 . Для каждого определенного вектора [ P ji , F ji ] приравняем значение вероятности P ji к атрибуту р_и соответствующей дуги eEPC модели. Таким образом, каждый вектор [ P ji , F ji ] в позиции f V матрицы F q описывает параметры GERT-сети, взятые из матрицы F 0 .

Определим функции распределения для дуг GERT-сети. Для V S j ,S j е B ₀( B ₀ е S ₀) возьмем атрибут t_bj . Согласно [5], вероятностное поведение системы бизнес-процессов адекватно описывает бета-распределение. Так как t_bj является средним значением времени выполнения функции b_j , то примем данное значение за математическое ожидание функции распределения времени выполнения дуги, выходящей из узла GERT-сети, соответствующего объекту «функция» модели eEPC.

Возьмем определенный на предыдущем этапе вектор [ p ji , F ji ] в позиции f V матрицы F V . Для каждого вектора, где V f V : s j- е B ₀ , определим F ji как функцию, описывающую бета-распределение с математическим ожиданием, равным t bj . Для каждого вектора, где соответствующий S j из F 0 не принадлежит B ₀ , функция F ji = 0 , то есть дуга e i является «холостой».

Таким образом, получены матрицы F 0 и F V , полностью отображающие GERT-сеть, соответствующую бизнес-процессу, описанному моделью ARIS eEPC.

Пример трансляции бизнес-процесса в GERT-сеть. Рассмотрим пример по трансляции бизнес-процесса «Изготовление детали» (рис. 4) в GERT-сеть.

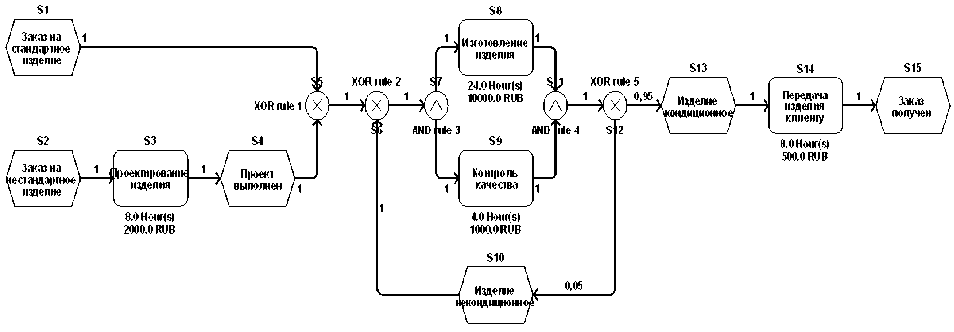
Рис. 4. Модель бизнес-процесса

В соответствии с алгоритмом трансляции выполним первичные преобразования моделей, данные преобразования приведены в таблице 3.

Преобразования объектов моделей

Таблица 3

Объект eEPC модели	Тип объекта eEPC модели	Узел GERT-сети	Тип узла GERT-сети
S1	Событие	V1	STEOR
S2	Событие	V2	STEOR
S3	Процесс	V3	STEOR
S4	Событие	V4	STEOR
S5	Перекресток	V5	STEOR
S6	Перекресток	V6	STEOR
S7	Перекресток	V7	[EOR, DT]
S8	Процесс	V8	STEOR
S9	Процесс	V9	STEOR
S10	Событие	V10	STEOR
S11	Перекресток	V11	[AND, ST]
S12	Перекресток	V12	STEOR
S13	Событие	V13	STEOR
S14	Процесс	V14	STEOR
S15	Событие	V15	STEOR

Для того чтобы воспроизвести первоначальную топологию GERT-сети, соответствующей транслируемой eEPC модели, приравняем матрицы инцидентности F 0E = F 0 и F V = F 0 .

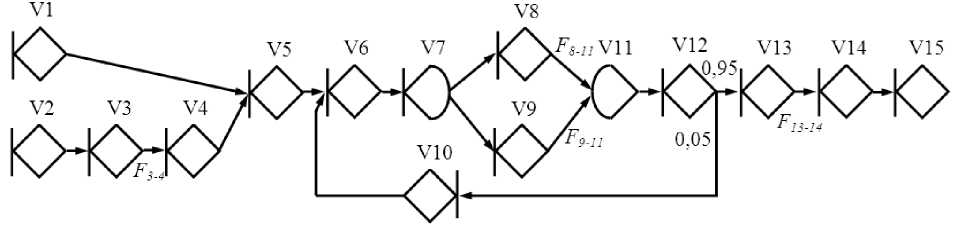
Рис. 5. GERT-сеть

Таким образом, получена сеть (рис. 5), структура которой соответствует eEPC модели исходного биз-нес-процесса. Для полной трансляции модели необходимо определить производящие функции на дугах GERT-сети в соответствии с числовыми параметрами исходного бизнес-процесса. Для этого выполним сопоставление, представленное в таблице 4, сопоставим параметры дуг GERT-сети с параметрами процесса модели eEPC.

Параметры GERT-сети

Таблица 4

Определяемый параметр GERT-сети f V ji	Вероятность pij дуги <  i , j >	Функция распределения F ij на дуге <  i , j >
f 3-3	1	F 3-4
f 8-9	1	F 8-11
f 9-10	1	F 9-11
f 14-16	1	F 13-14
f 12-14	0,95	-
f 12-12	0,05	-

Заключение. Таким образом, предложен алгоритм, позволяющий однозначно конвертировать матричную форму описания модели бизнес-процессов в формате ARIS eEPC в матричную форму описания GERT-сети.

Полученная GERT-сеть позволяет исследовать и анализировать вероятностное поведение бизнес-процессов и получать их вероятностные характеристики: математическое ожидание и дисперсию времени выполнения.