Алгоритм управления профилем кристалла для автоматического выращивания методом Чохральского

Для получения кристаллов высокого качества современная ростовая установка должна оснащаться автоматической системой управления (АСУ) процессом выращивания.

Качество кристаллов, получаемых методом Чохральского [1], во многом зависит от формы конуса расширения, формы участка перехода к необходимому диаметру слитка и, наконец, формы заужения кристалла. В связи с этим в настоящее время ведутся разработки автоматических систем, осуществляющих точный контроль и управление формой всех участков профиля кристалла.

Для тугоплавких оксидов наибольшее распространение получили системы управления с весовым контролем выращиваемого кристалла и регулированием мощности ВЧ генератора (так называемый Т-канал).

Бардсли У. и соавторы [2] предложили уравнение наблюдения (1), описывающее силу, действующую на датчик веса:

t

W ^{( t} ) = J P s g ^{n R} 2 ^{( t ) V}c ^{( t} ) d t +

+ PignRC (t) h (R (t )e (t))+

+ 2 n R ( t ) o l cos 6 l ( t ) ,                 (1)

где W ( t ) — сила, регистрируемая датчиком веса; p _s, p l — плотности кристалла и расплава; R — радиус кристалла; R c — радиус тигля; о l — коэффициент поверхностного натяжения расплава; e l (t) — угол наклона боковой поверхности мениска; V c (t) — скорость кристаллизации; h(R(t), e l (t)) — высота мениска. Первое слагаемое соответствует весу

кристалла, второе и третье определяют вес мениска высотой h.

Высота мениска зависит от радиуса кристалла и угла роста. Для ее определения используется формула Цивинского С.В. [3]

( h (R, el )= a 1 - sin el +

a cos e l

1/2

V a2 cos el

16 R ²

/

4 R

,

a =

( 2.0

' i )

V pig J

.

Существует ряд работ, посвященных системам

управления ростом кристаллов с использованием уравнения наблюдения (1). В работе [4] автоматический контроль за радиусом растущего кристалла осуществляется в предположении цилиндрического роста ( e l = 0). Для определения реального радиуса кристалла авторы дифференцируют уравнение (1), отбрасывают члены, учитывающие динамику мениска, и получают уравнение, связывающее величину силы, действующей на датчик веса, с радиусом кристалла:

W ( t ) = P s g n R ² ( t ) V c . (3)

Однако этот метод контроля неприменим для выращивания кристаллов с заданной формой участков разращивания и заужения.

Способом автоматического управления обеспечивающим рост кристалла с заданным профилем боковой поверхности является управление, при котором реальная сила сравнивается с опорной (расчетной) величиной силы. В работах [5, 6] предложен итерационный способ расчета программной силы на основе уравнения наблюдения (1). Скорость кристаллизации, входящая в это уравнение, представлена в виде аналитической

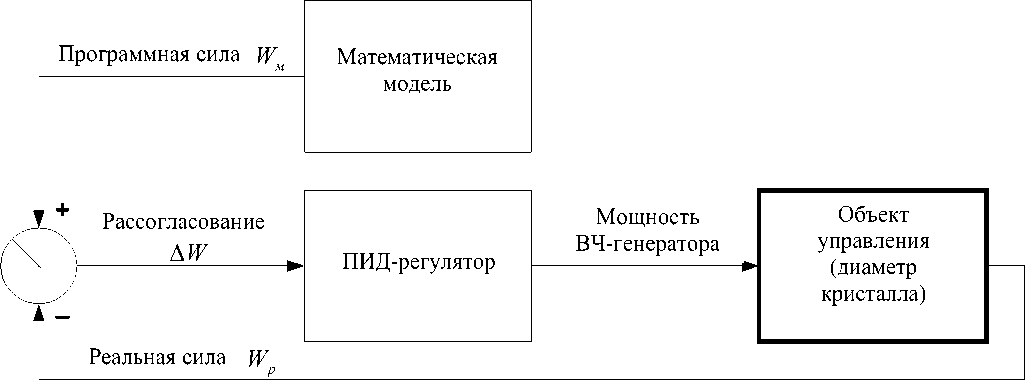
Рис. 1. Блок-схема системы автоматического управления ростом кристалла

функции. При этом профиль кристалла задается в виде полинома или гладкой тригонометрической функции, а его изменение определяется выбором соответствующих коэффициентов.

Целью настоящей работы является создание алгоритма автоматического управления для выращивания кристаллов заданного профиля, в котором при расчете программной силы форма кристалла может быть задана как численно, так и в виде аналитической функции.

АЛГОРИТМ УПРАВЛЕНИЯ

Для выращивания кристалла с произвольным профилем R(l) нами была применена система автоматического управления с использованием опорного сигнала программного веса кристалла. Блок-схема АСУ представлена на рис. 1.

Опорное значение веса рассчитывается программой из уравнения наблюдения (1). Полученная величина сравнивается с реальной силой, действующей на датчик веса кристалла. Величина рассогласования поступает на пропорционально-интегральнодифференциальный регулятор (ПИД-регулятор), осуществляющий управление по Т-каналу.

Для вычисления уравнения наблюдения (1) необходимо сделать переход от зависимости изменения радиуса по длине кристалла к зависимости изменения радиуса кристалла во времени R(l) ^ R(t). Программная длина l, выращенного за время t кристалла, состоит из перемещения штока со скоростью V 0 плюс падение расплава в тигле и минус высота мениска h . В общем случае зависимость длины выросшего кристалла l от времени носит нелинейный характер (рис. 2):

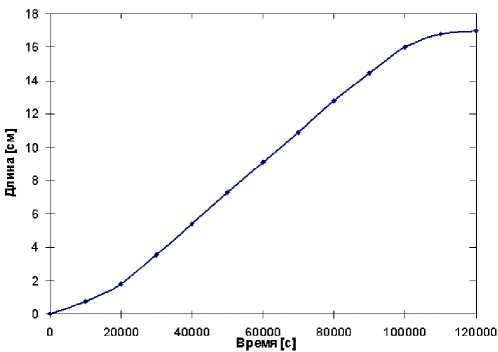
Рис. 2. Пример изменения программной длины кристалла от времени для V 0 = 4 мм/ч, R c = 5 см, а = 0.6 см

l

l = V01 +           2 (l) dl - h (R ()’ 6l (l)),     (4)

P l^Rc 0

где R c — радиус тигля.

Запишем время достижения кристаллом длины l при постоянной скорости вытягивания V 0 :

= -1 l + h (R (l), 6, (l))

V ₀

V

-

P s

P l R

l

_T J R ² ( l ) d l .

c 0

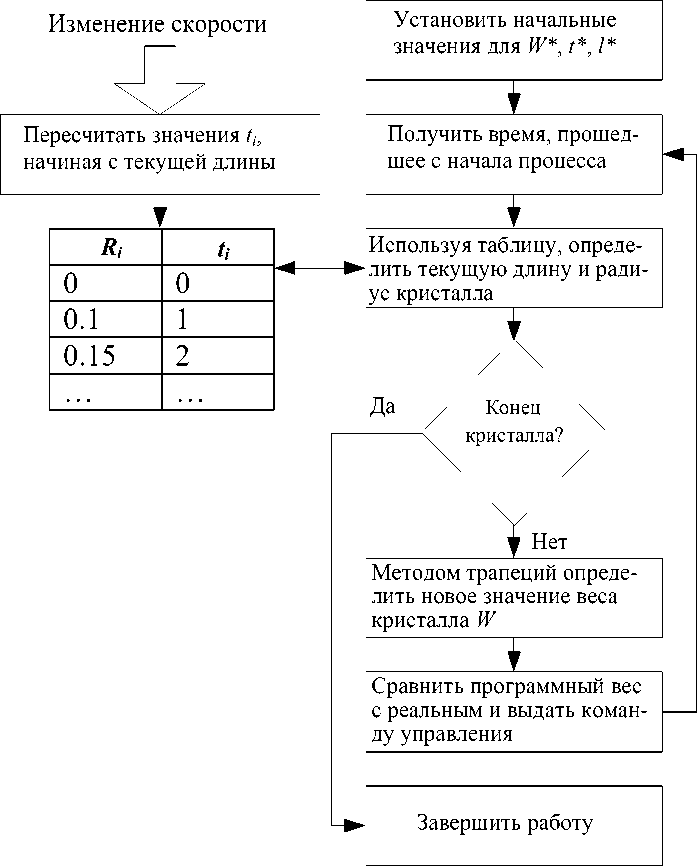
Рис. 3. Блок-схема алгоритма управления

При достаточно малом разбиении по длине кристалла интеграл в выражении (5) можно заменить суммой. В случае интегрирования методом трапеций выражение (5) примет вид:

t i ( l i , V 0 ) = 1- ( l. + h i ^ R i , ® !? )-

V0

-

V 0

P s

P l R C

A l

n ( i, ) - 1

K R 2

j = 1

+ R 2 - 1 ) ,

где

l =(i±1) i , = q_ n — i, (7) i N max причем lmax — максимальная модельная длина кристалла, N — количество точек разбиения по модельной длине кристалла.

Рассмотрим основной цикл работы программы по управлению ( рис . 3). Перед началом работы цикла регулирования в программе создается мас сив , в ячейки которого заносятся значения R i (l i ) и t i ( времена достижения дискретной длины кристалла l_i при постоянной скорости вытягивания V₀), вычисленные по формуле (6); производится ини -

циализация начальными значениями переменных W^*, t^* и l^* — текущих величин управления.

В цикле управления происходит оп _* рос таймера компьютера, и вычисление времени t^* , прошедшего с начала процесса. По этому времени осуществляется поиск в массиве t i таких значений t i–1 и t i , что *_i-1 <  * < t i . Определенный в ходе поиска индекс массива i используется для нахождения из таблиц величин l i–1 , l i , R i–1 , R i , h i–1 , h i .

В ходе циклов управления процессом рост _* а кристаллов, возможен случай, когда время t^* , прошедшее с начала процесса, попадает в тот же интервал [ t i–1 , t i ), что и на предыдущем цикле. Поэтому для увеличен _* ия точности вычисления про- _* граммной длины l^* , программного радиуса R^* и программной высоты мениска h^* используем линейную интерполяцию (8), (9), (10) на отрезке [ t i–1 , t i ):

l = 7—i 1 (* - ti-1)+ li-1, i i-1

R • = RL-R,-1 (,• — ti- )+ Ri-1,(9)

i i - 1

h. h- h = ti /—1 (* — ti—1)+ hi—1.

i i — 1

ее ручной корректировке оператором система управления осуществляет пересчет величин t_i по выражению (13), начиная с элемента массива с текущим индексом i :

ti^{( l}i , V о ) = * ^{+     (} i ^{— l )+}

V ₀

+ h ⁽ R„ Qi?)-

V ₀

— -— — ⁽ У ( ^Rj ² + Rj ² J-     (13)

V о P i R C 2 ^^.^V j     j ^{— —} ’

В управляющей программе для визуализации ростового процесса [6] производится решение обратной задачи: вычисление реального радиуса растущего кристалла R^r по сигналу с датчика веса. Вычисление реального радиуса основано на предположении о линейном изменении реального радиуса за цикл управления. Предполагая, что программная длина кристалла l^* равна реальной длине l^r и программный вес мениска равен реальному весу мениска, получим квадратное уравнение для нахождения R^r :

r * + r; — 1 r * +

Для обозначения реальных и программных величин на разных циклах управления введем индекс цикла t . Тогда R_t ^* , l_t ^* , h_t ^* — программные величины на текущем цикле управления, a R* _{— 1} , l* _{— 1} , h* _{— 1} — на предыдущем. Используя формулу для объема усеченного конуса, вычисляем программный вес кристалла W^* :

(

+ R^rt — 1

v

3 ( W r - W_t m - W_t\ + W m )) -V- **-,* —Ц * —12

Pn ( l * — l *^ )

s *     * — 1

= 0,

где W _t ^m — программный вес мениска на текущем

цикле управления, W _t ^r — сигнал с датчика веса.

W * * = <1 +

+ P_s n s ₃

*

X*

— 1₁ JIl R + R_t ,R_t +(R_t fl.    (11)

* —1 / \V * —1 /           * —1 *      \ i / 1        \ /

Далее программный вес W _t ^* поступает на сравнивающее устройство, которое определяет величину рассогласования программного веса кристалла и сигнала, снимаемого с датчика веса. Величина рассогласования A W из сравнивающего устройства поступает на ПИД-регулятор, осуществляющий регулирование по T-каналу (12),

t *

P = k„АW + k_t A W d t + k_d d^W pi   d

.

В случае программного изменения скорости вытягивания V 0 по определенному закону или при

ВЫВОДЫ

Предложенный в этой статье алгоритм вычисления программного веса кристалла был применен в управляющей программе Nika-2000 для ростовой установки NIKA, выпускаемой Экспериментальным заводом научного приборостроения РАН.

Использование данного алгоритма позволяет: выращивать переходные участки профиля кристалла в автоматическом режиме; рассчитывать текущий реальный радиус кристалла; осуществлять визуализацию процесса роста [7]; производить переход в режим автоматического управления процессом кристаллизации с произвольной точки профиля кристалла. В ростовой программе на основе описанного алгоритма реализована возможность изменения скорости вытягивания непосредственно в процессе выращивания.

С помощью АСУ на основе данной реализации уравнения наблюдения были успешно выращены

кристаллы алюмоиттриевого граната. На рис. 4 представлен один из них.

Выращенные кристаллы исследовались на профилометре для определения отклонения реального радиуса от заданного. Величина отклонения радиуса от номинального значения составила ± 0.5 мм. На рис. 5 представлены фотография конуса разращивания и профильная кривая.

Рис. 4. Выращенный кристалл алюмоиттриевого граната. Длина приблизительно 40 см