Алгоритм управления упруго-вязко-пластичной моделью для исследования процессов ударного взаимодействия тел

УДК 620.179                                              

Control algorithm for an elastic-viscoplastic model to study processes of shock interaction of bodies

• V. L. Lapshin¹, E. V. Zenkov^1,2

• ¹    Irkutsk National Research Technical University (Irkutsk, Russian Federation)

• ²    Irkutsk State Transport University (Irkutsk, Russian Federation)

Introduction. In engineering practice, dynamic processes, with the help of which mechanics of interaction of machine components and structural elements are described and studied, are of great importance. These dynamic processes are the

Информатика, вычислительная техника и управление

cause of large deformations leading to the destruction. The research objective is to develop a more accurate shock simulation algorithm through the controlled transformation of the mechanorheological shock process model from elastic-viscous to elastic-viscoplastic.

Materials and Methods. Differential equations of the model movement are proposed. The conditions for the transformation of the model during the transition from elastic to plastic deformations, from the stage of loading the model to the stage of unloading under the shock interaction with the surface, are considered. When calculating deformations, the assumption is made that elastic and plastic deformations occur simultaneously from the very onset of the impact. The model functioning method is considered in detail, the algorithm of the model operation is developed, the logic of its functioning is described in detail.

Results. To study shock processes, a mechanoreological elastic-viscoplastic model was developed. An important parameter of the model is the force corresponding to the onset of plastic deformation. As a result of the research, a more perfect algorithm was created, and a new computer program was developed to study the shock process using an elastic-viscoplastic model with an adjustable elastic-plastic transformation.

Discussion and Conclusions. The results obtained can be used to improve the accuracy and reliability of simulation of shock processes in order to further develop the techniques for determining the physical and mechanical characteristics of materials by shock methods. Knowledge of the mechanical characteristics of materials is required when solving various research problems through mathematical modeling of vibration and shock processes. At the same time, an important task is to adapt the design model to the real shock process, for which it is required to develop appropriate methods and techniques.

Введение . В инженерной практике важное значение имеют динамические процессы (ударные, вибрационные). С их помощью описывают и изучают механику взаимодействия деталей машин и элементов конструкций. При этом большое внимание уделяют ударным процессам, так как при этом тела подвергаются действию больших динамических нагрузок. Они могут являться причиной больших деформаций и приводить к разрушению оборудования. Данные обстоятельства объясняют повышенное внимание к моделированию и исследованию динамических процессов со стороны ученых и инженеров [1–14]. Особый практический интерес имеет развитие экспресс-методик и способов определения физико-механических характеристик материалов ударными методами. При этом важной задачей является адаптация расчетной модели к реальному ударному процессу. В связи с этим целью исследования является создание более точного алгоритма моделирования ударного процесса за счет управляемого преобразования механореологической модели ударного процесса из упруго-вязкой в упруго-вязко-пластичную. Разработанный алгоритм позволяет на этапе нагружения осуществлять преобразование модели на основе заданных условий, что обеспечивает более качественное и достоверное моделирование ударного процесса с учетом реальной пластичности материала. Предыдущая разработка не позволяла осуществить данное преобразование и модель при ударном взаимодействии являлась упруго-вязко-пластичной с самого начала нагружения.

Материалы и методы. Одним из направлений научных исследований в Иркутском национальном исследовательском техническом университете является моделирование и изучение процессов динамического взаимодействия твердых тел. Для изучения динамики протекания данных процессов с целью решения практических задач разработана и исследована упруго-вязко-пластичная модель [15]. Модель построена с использованием реологических и инерционных элементов m 1 и m 2 , объединенных в два блока (рис. 1). Один из блоков является упруго-вязким К 1 – С . Он предназначен для моделирования упругих деформаций тела. Они возникают под действием внешней нагрузки и исчезают при ее отсутствии. Упруго-пластический блок К 2 – f 2 моделирует пластические деформации, остающиеся после снятия нагрузки. Масса тела учитывается инерционным элементом m 1 . Масса m 2 введена для того, чтобы описывать динамику движения упруго-вязкопластичной модели с помощью двух дифференциальных уравнений второго порядка. Чтобы исключить влияние m 2 на динамику процесса, ее величина принималась малой ( m 2 ≤ 0,001 m 1 ). Как показали расчеты, при таком условии можно принять N 1 ≈ N 2 (4).

Рассмотрим ударный процесс на примере сферического тела. При нагружении тела в нем возникают внутренние силы, препятствующие изменению формы и размера тела, то есть препятствующие (2) его деформации. Одной из них является сила сопротивления упругой деформации. При этом могут возникать дополнительные сопротивления деформации, которые называются вязкими. Они связаны со скоростью деформации тела. На модели данные сопротивления деформации тела описываются выражениями:

N i = F v + F e . ,

F v = С ( У 1 - У 2 ) ‘ Ч У 1 — У 2 ) ‘ 2 ,                                                (1)

F e 1 = К i (y 1 - y 2 ) 1 .

где y ₁, y ₂, y ₁, y ₂ — динамические характеристики модели, описывающие перемещение и скорость инерционных элементов m 1 и m 2 ; К 1 — параметр модели, характеризующий упругие свойства материала (упруго-вязкого блока модели); C — параметр модели, характеризующий вязкие (диссипативные) свойства материала в том же блоке модели (3).

Силы сопротивления деформации, возникающие в упруго-пластическом блоке модели, описываются следующими выражениями:

N 2 = F_P + F e 2 ;N 2 « N 1 ;

n2

F e 2 = К 2 У 2 ;                                                         (2)

F p = f 2 У 2 n + F st .

Здесь F ST — усилие нагружения модели, при котором начинает работать упруго-пластический блок модели, учитывающий пластические деформации материала; К 2 — параметр модели, характеризующий упругие свойства материала при пластической деформации (упруго-пластического блока модели); f 2 — параметр модели, характеризующий пластичность материала в том же блоке модели (3).

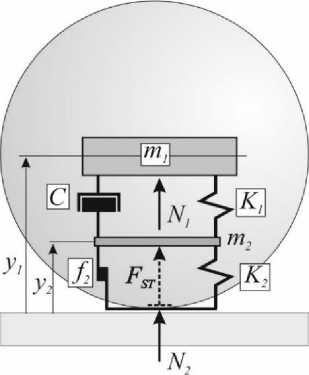
Рис. 1. Упруго-вязко-пластичная механореологическая модель •

Переменные y ₁ , y ₁ описывают величину и скорость полной (суммарной) деформации. Переменные

• y2 , y2 описывают величину и скорость пластической деформации. Следовательно, скорость и величина

• •       •

упругой деформации определяется как y 1 - у ₂; у 1 - у ₂.

Реологические элементы модели (упругий, вязкий, пластичный) имеют нелинейные характеристики, то есть упругие, вязкие и пластические сопротивления деформации пропорциональны скорости и величине деформации в заданной степени ( s 1 , s 2 , n 1, n 2 , n 3 ). В качестве рекомендации можно отметить, что для упругих сопротивлений при ударе сферического тела следует использовать n 1 = n 2 =3/2 [2–4], для вязких и пластических сопротивлений можно принять значение равное единице [2, 3].

Результаты исследования. Рассмотрим работу модели. На начальном этапе использования модели в научных исследованиях использовался упрощенный вариант ее функционирования. Принималось условие, что при деформации тела упругие и пластические деформации возникают одновременно с самого начала нагружения. Это позволило разработать и опробовать на практике более простой алгоритм функционирования

Информатика, вычислительная техника и управление

модели. На его основе была разработана исследовательская компьютерная программа ¹ , выполнен комплекс научных исследований ударного процесса на модели ² , в том числе представленных в работе [16].

Однако данное упрощение ограничивает возможности модели и не позволяет в полном объеме выполнять исследования ударных процессов. Поэтому в результате дальнейших исследований был создан более совершенный алгоритм и разработана новая компьютерная программа для исследования ударного процесса с помощью упруго-вязко-пластичной модели с регулируемым упруго-пластическим преобразованием ³ . Рассмотрим этот алгоритм функционирования модели более подробно.

Разработанный алгоритм обеспечивает следующую последовательность функционирования блоков модели. На начальном этапе ударного процесса в работе участвует только упруго -вязкий блок модели К 1 - С . Он позволяет рассчитать упругие деформации тела на этапе нагружения (рис. 2). При этом упруго-пластический блок модели не функционирует, так как до определенного момента пластические деформации в теле могут отсутствовать. Появление пластических деформаций соответствует заданному усилию F ST . Когда расчетное усилие нагружения N 1 достигнет заданного значения ( N 1 = F ST ), упруго-вязкая модель преобразуется в упруговязко-пластичную. Начинает функционировать упруго -пластический блок модели. Когда усилие нагружения достигает своего максимального значения N max , рост деформации прекращается и этап нагружения заканчивается. За счет упругости материала тело начинает восстанавливать свою первоначальную форму и размеры, наступает этап разгрузки модели. В ходе этого процесса исчезают упругие деформации, при этом возникшие пластические деформации остаются в теле и, соответственно, на модели. Таким образом на этапе разгрузки модели работает только упруго-вязкий блок.

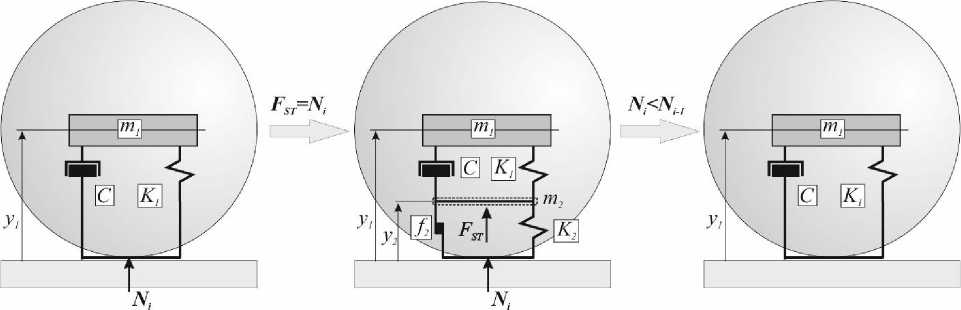
Рис. 2. Схема преобразования модели

Этап контактного взаимодействия заканчивается, когда сила нормальной реакции N , определяемая уравнениями (1) и (2), становится равной нулю. Тело отскакивает от поверхности на высоту h .

Процесс нагружения модели на различных этапах деформирования описывается с помощью дифференциальных уравнений, которые приводятся ниже:

т1 У; + С1У1 Уi + K1У1 n1 — m^g ,(3)

• • •             ••

ml У1+ C1(У1 - У 2) s1 (У1 - У 2) s2 + K1(У1 - У 2) n1 = - ml g ,

• ••                                                 ••

m2 y 2 + K2y2n2 + f;y2n3 + C (y 2 - y 1)s1 (y 2 - y 1)s2 + K1 (y2 - У1)n1 =-m2g + F^ .(5)

С помощью уравнения (3) рассчитываются упругие деформации модели на этапах нагружения и разгрузки. С помощью уравнений (4) и (5) рассчитываются упругие и пластические деформации модели при ее нагружении на этапе пластического деформирования материала.

Сила нормальной реакции на этапе упругой деформации определяется по формуле:

• • s 1 s 2

N i = Су 1 у 1 + K 1 y ; 1 .                                            (6)

Сила нормальной реакции на этапе пластической деформации определяется по формуле:

n 3

Ni= K2у2n2 + f; у2 + Fst .(7)

Вычисление производится с заданным временным шагом dt . Время удара определяется по формуле:

T = dt • г,(8)

где i — количество шагов.

Условие перехода от упругой деформации к пластической имеет вид:

N > FSt(9)

Условие окончания этапа нагружения и начала этапа разгрузки модели:

<>> N(10)

Условие окончания этапа контактного взаимодействия модели:

N= 0(11)

Рассмотрим алгоритм исследования ударного процесса (рис. 3).

• 1.    Блок 1 формирует исходные данные исследуемого процесса.

• 2.    Блок 2 вводит исходные данные процесса: начальное время удара t = 0, начальную деформацию тела ••

• 3.    Блок 3 выполняет вычисление значений коэффициентов модели K 1 , K ₂, f₂ , C .

• 4.    Блок 4 выполняет вычисление времени удара и фиксирует количество шагов расчета на этапе нагружения при упругой деформации.

• 5.    Блок 5 выполняет вычисление параметров процесса ударного взаимодействия тел с помощью

• 6.    Блоки 6 и 16 осуществляют проверку по условию (11). При невыполнении условия расчет продолжается на следующем шаге этапа ударного взаимодействия. Если условие выполняется, то расчет завершается и выполняется переход к этапу отскока модели.

• 7.    Блоки 7 и 12 контролируют момент завершения процесса нагружения модели. Выполнение условия (10) означает, что этап нагружения модели закончился, сила контактного взаимодействия N i начинает уменьшаться. Выполняется расчет на этапе разгрузки модели. Вычисление передается блоку 4 или 14. При невыполнении условия (10) сила контактного взаимодействия N i продолжает увеличиваться. Этап нагружения модели продолжается и вычисление производят блоки 8 или 13.

• 8.    Блок 8 фиксирует наибольшую величину силы контактного взаимодействия N max , соответствующее ей время в процессе удара T_Nmax и передает управление блоку 9.

• 9.    Блок 9 определяет окончание этапа упругой деформации при нагружении модели. Если условие (9) выполняется, значит сила нормальной реакции модели N i превышает заданное усилие F_st , соответствующее началу образования пластических деформаций. Этап упругой деформации завершается, начинается этап упруго-пластической деформации и управление передается блоку 10. Если условие (9) не выполняется, значит сила нормальной реакции модели N i меньше заданного значения F st и пластические деформации отсутствуют. Вычисление передается блоку 4 для выполнения расчета на следующем шаге этапа упругой деформации.

• 10.    Блок 10 производит расчет текущего времени и номера шага вычисления на этапе упруго -пластической деформации.

• 11.    Блок 11 выполняет вычисление параметров процесса ударного взаимодействия тел на этапе

• 12.    Блок 12 определяет окончание этапа нагружения модели. Если условие (10) выполняется, значит сила нормальной реакции N i уменьшается, этап нагружения модели закончился и выполняется переход к этапу разгрузки модели. Управление передается блоку 14. Если условие (10) не выполняется, значит сила нормальной реакции N i продолжает увеличиваться, идет этап нагружения модели и управление передается блоку 13.

• 13.    Блок 13 фиксирует наибольшую величину силы контактного взаимодействия N max и соответствующее ей время в процессе удара T Nmax и передает управление блоку 10 для расчета на следующем шаге этапа упруго-пластической деформации.

• 14.    Блок 14 производит расчет текущего времени и номера шага вычисления на этапе упругой деформации при разгрузке модели. Управление передается блоку 15.

  Информатика, вычислительная техника и управление

  
  

• 15.    Блок 15 выполняет расчет параметров процесса ударного взаимодействия тел с использованием

• 16.    Блок 16 осуществляет проверку условия (11). При невыполнении условия этап ударного взаимодействия продолжается и управление передается блоку 14. При выполнении условия расчет на этапе ударного взаимодействия завершается и осуществляется переход к этапу отскока модели. Управление передается блоку 17.

  
  
  

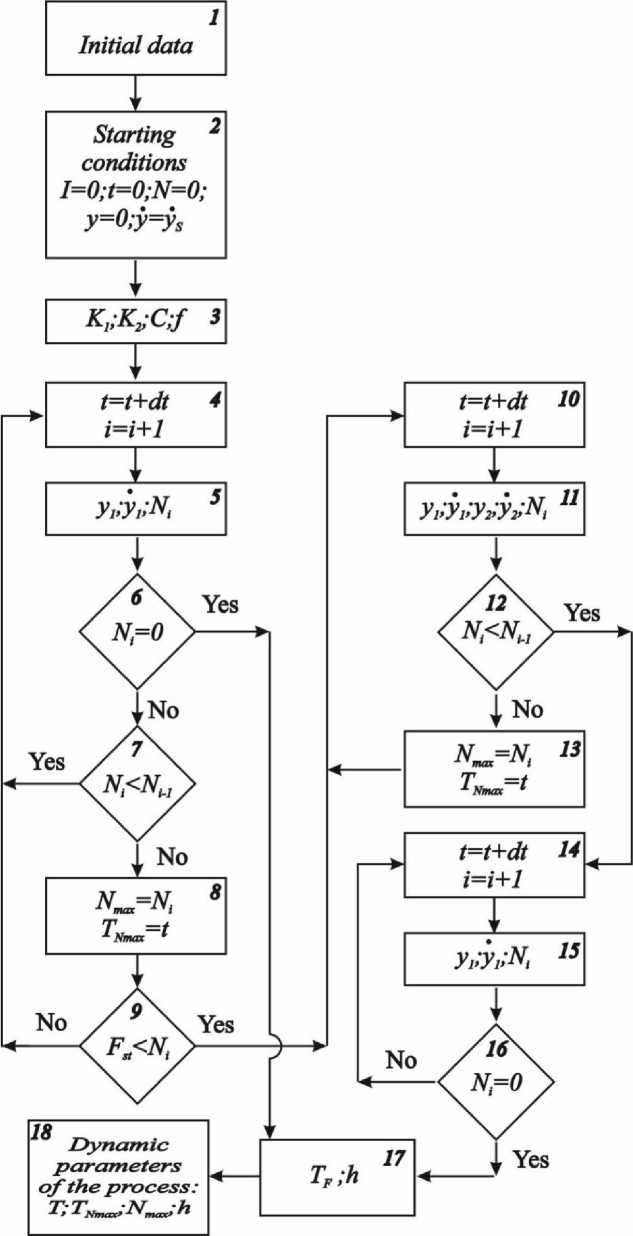
  Рис. 3. Схема алгоритма

  
  

• 17.    Блок 17 определяет высоту отскока тела h , время полета при отскоке T F и передает управление блоку 18.

• 18.    Блок 18 формирует и выводит основные характеристики ударного процесса: время ударного взаимодействия тел (модели) T (уравнение (8)); силу ударного взаимодействия тел N max ; время в процессе удара T Nmax , соответствующее N max ; высоту отскока тела (модели) h .

(модели) у = 0, начальную скорость деформации у = y_s , начальную силу удара N = 0.

• упруго-вязкого блока модели. Рассчитывается упругая деформация у 1 и скорость деформации у 1 (уравнение (3)). Определяется сила ударного взаимодействия Ni (уравнение (6)).

•            • пластического деформирования. Рассчитываются скорости и величины деформаций модели у,,у,,у2,у2 (уравнения (4) и (5)), определяется сила контактного взаимодействия Ni (уравнение (7)). Далее управление передается блоку 12.

упруго-вязкой модели при разгрузке: упругой деформации y 1 , скорости деформации y ₁ по уравнению (3), силы нормальной реакции N i по уравнению (6). Управление передается блоку 16.

На базе разработанного алгоритма была создана исследовательская компьютерная программа ⁴ . С использованием авторской программы были выполнены исследования процесса ударного взаимодействия тел [17]. Изучалось влияние различных факторов на динамику ударного процесса. В частности, на модели изучалось влияние механических свойств материала (упругости, вязкости, пластичности) на время и силу ударного взаимодействия сферического тела с поверхностью, величину и скорость деформации, высоту отскока после удара. При этом рассматривались различные варианты упруго-пластического преобразования исследовательской модели, отражающие переход из упругого в упруго-пластическое состояния материала при нагружении.

Сравним работу упруго-вязко-пластичной модели по предыдущему (график 1, рис. 4) и новому (график 2, рис. 4) алгоритму.

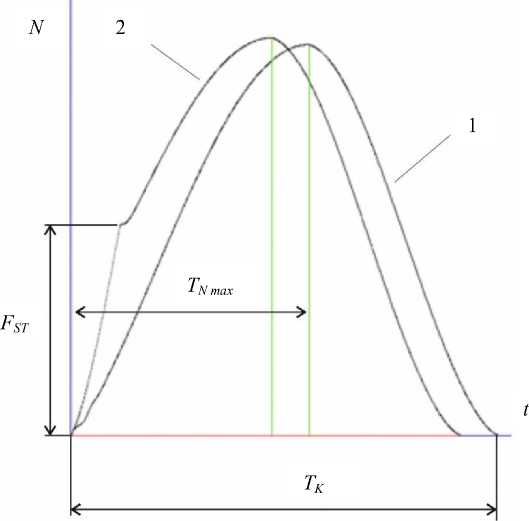
Рис. 4. Изменение силы ударного взаимодействия тел N

Новый алгоритм позволяет при моделировании ударного процесса взаимодействия тел осуществлять переход от упруго-вязкой модели к упруго-вязко-пластичной модели по заданному усилию ударного взаимодействия F ST . Этот переход на модели соответствует началу образования вматериале пластических деформаций, что позволяет описывать ударный процесс более достоверно и точно. Хорошо видно, что закономерность изменения силы нормальной реакции, рассчитанная по новому алгоритму (график 2, рис. 4), существенно отличается от аналогичной закономерности (график 1, рис. 4), полученной на предыдущем варианте алгоритма. Отличается время удара T K и время от начала удара до максимума силы ударного взаимодействия T Nmax (рис. 4). Может существенно изменяться и величина N max . Таким образом, разработанный алгоритм позволяет более качественно решать вопросы адаптации упруго-вязко-пластичной модели к реальным процессам ударного взаимодействия тел с учетом их механических свойств.

Заключение . В результате исследований был создан более совершенный алгоритм и разработана новая компьютерная программа для исследования ударного процесса с помощью упруго -вязко-пластичной модели с регулируемым упруго -пластическим преобразованием. Представлены дифференциальные уравнения движения модели. Рассмотрены условия преобразования модели при переходе от упругих к пластическим деформациям, от этапа нагружения модели к этапу разгрузки при ударном взаимодействии с поверхностью. Подробно рассмотрена методика функционирования модели, составлен алгоритм работы модели, подробно описана логика его функционирования.

Информатика, вычислительная техника и управление

Преимуществом нового алгоритма является то, что он позволяет более точно описать процесс в момент начала образования пластических деформаций в материале при его нагружении. Момент начала пластических деформаций на модели может быть точно задан и полностью соответствовать фактическому поведению материала. Для этого, например, можно использовать данные экспериментальных исследований ударного процесса. В предыдущих версиях алгоритма и программы такая возможность отсутствовала.

Так, например, для исследования ударного процесса взаимодействия сферического тела с поверхностью был разработан алгоритм адаптации упруго-вязко-пластичной модели к условиям ударного процесса взаимодействия тел 5 .

В данном алгоритме было реализовано условие, при котором упругие и пластические деформации возникают одновременно с самого начала ударного взаимодействия. Однако данное упрощение реального процесса ограничивает возможности моделирования, особенно при изучении влияния пластичности материала на динамику ударного процесса.

Усовершенствованный алгоритм позволяет реализовать возможности упруго-вязко-пластичной модели в полном объеме. Упруго-пластическое преобразование модели может быть выполнено по заданному плану, что обеспечит более качественную адаптацию модели к реальному ударному процессу. При этом фактические пластические деформации могут быть смоделированы более достоверно.

Таким образом, новый параметр модели F ST (усилие нагружения, соответствующее появлению в материале пластических деформаций), введенный с помощью разработанного алгоритма, расширяет возможности адаптации модели к реальным ударным процессам и повышает точность модели при описании пластических деформаций. Работоспособность алгоритма была подтверждена в ходе проведения исследований ударного процесса с помощью модели [18].

Практическое применение разработанной программы может существенно повысить точность и достоверность моделирования ударных процессов. В частности, результаты исследований ударных процессов могут являться базой для совершенствования методик и способов оценки механических свойств конструкционных материалов, основанных на ударном принципе действия. Так, на основе предыдущей версии алгоритма был разработан новый способ определения модуля упругости материала, основанный на ударном взаимодействии тел [16]. Знание механических свойств материалов необходимо при выполнении исследований для формирования математических моделей процессов вибрационного и ударного взаимодействия механических систем. При этом важной задачей является адаптация расчетной модели к реальному ударному процессу, для чего необходима разработка соответствующих способов и методик. Решение данных задач возможно на основе полученных результатов исследований.