Алгоритм уточняющего прерывания для систем имитационного моделирования с дискретными событиями

• 1 . Описание тестовой задачи. При создании имитационных моделей в парадигме дискретных событий с переменным временным шагом требуется максимально точно вычислить время возникновения следующего события. Такие расчеты выполнить сложно, поскольку в общем случае необходимо учитывать состояние всей имитационной модели. Для упрощения этих вычислений применяются различные соглашения, которые, как правило, снижают качество моделирования и могут использоваться не для всех ситуаций, возможных в модели.

Приведем описание двух задач. Эти задачи являются реальными и поэтому достаточно сложными. Кроме того, эти две задачи содержат описание функциональности, которая хорошо иллюстрирует применение предлагаемого алгоритма.

Задача 1. Предположим, требуется создать имитационную модель сложной складской конвейерной сети, транспортирующей стопки картона различного размера. Используется подход, описанный в [1]: декомпозиция исходной технологической системы представляет собой элементарную модель конвейера (ЭМК). Такая элементарная модель имеет вход и выход, описывающие линейные размеры (длину) и скорость движения ленты транспортера. Несколько экземпляров элементарной модели могут быть соединены своими входами и выходами. Помимо ЭМК нужно построить имитационную модель программы управления этой технологической системой.

Продуктом в имитационной модели являются стопки картона, которые каким-либо образом должны перемещаться по соединенным между собой экземплярам ЭМК. Далее эти стопки будем называть транспортными блоками (ТБ).

Для генерации и удаления ТБ из системы применяются ЭМК специального вида — входные и выходные конвейеры. Каждому созданному ТБ присваивается путь, который начинается на входной ЭМК и заканчивается либо на выходной, либо на одной из внутренних ЭМК.

В данном случае ЭМК выступает в качестве “складирующей”. Модель системы управления может принимать решение о передаче ТБ с одной ЭМК на другую в соответствии с путем в ТБ и с загрузкой каждого ЭМК. В дальнейшем система управления может использовать “складированный” ТБ для доставки его на выход системы.

Осложняющим фактором является то, что любая ЭМК может иметь от одной до четырех “линий”, каждая из которых, по сути, является самостоятельным конвейером и может включаться индивидуально. ТБ имеют различные линейные размеры и могут помещаться как на одну, так и на несколько линий, образуя таким образом сложные “упаковки”. Для предотвращения опрокидывания ТБ применяется сложный алгоритм его передачи с одной ЭМК на другую, включающий синхронизацию скоростей ЭМК, небольшой “наезд” новой ТБ на неподвижную ЭМК и т. д.

Имитационный эксперимент формулируется следующим образом: для произвольной заданной топологии конвейеров определить следующие характеристики:

• —    максимальное количество ТБ, которое может быть складировано в течение 1 ч работы;

• —    максимальное время, необходимое для полного освобождения полностью загруженного склада;

• —    вероятность того, что данная топология ЭМК приведет к образованию “пробок” из ТБ; изменения, которые необходимо внести (добавить дополнительные ЭМК), чтобы система функционировала без “пробок”.

• 2. Алгоритм уточняющего прерывания. В обеих задачах основной трудностью является имитация движения продукта (машины или ТБ) по системе (модель дорожной сети или соединенные между собой экземпляры ЭМК). Событиями в имитационных моделях этих задач будем считать изменения состояний подвижных объектов: в задаче 1 — состояние ЭМК (для каждой из четырех “линий” это разгон, движение, торможение, останов), в задаче 2 — состояние машины (разгон, торможение, движение, останов), связанное с изменением окружающей обстановки или необходимостью изменить характер движения. Такие подвижные объекты будем называть субъектами модели.

Задача 2. Другой похожей задачей является имитация потока машин на микроуровне, описанная в [2]. Как указано в данной работе, основной проблемой в построении такой имитационной модели является то, что “ . . . расчет нового состояния транспортного средства необходим каждый раз при изменении какого-либо из окружающих факторов,... при расчете нового состояния необходимо учитывать влияние всех факторов одновременно”.

В задаче 2 продуктом являются машины.

Задача для имитации: необходимо определить изменения в дорожной топологии (новые развязки или дороги, изменение работы светофоров), которые могут привести к улучшению дорожной ситуации (увеличению средней скорости потока машин).

Существуют следующие способы расчета времени до следующего события.

Способ 1 (простой) . Требуется рассчитать момент времени следующего события для данного субъекта имитационной модели исходя только из его внутренних, текущих данных: дистанции ТБ на экземпляре ЭМК или расстояния до пункта назначения для машины. Очевидно, что такой способ можно применять без модификации только в условиях гарантированного отсутствия конфликтов (столкновений) при движении продукта. В приведенных выше задачах представляют интерес именно такие конфликты.

Способ 2 (сложный). Требуется рассчитать момент времени следующего события на субъекте, учитывая, по крайней мере, состояние окружающей среды (для субъекта): сведения о загрузке и текущем состоянии всех соседей ЭМК или сведения о состояниях всех машин в каком-либо радиусе для субъекта машины. Данный способ, в отличие от способа 1, учитывает возможности различных конфликтов (столкновений) и может применяться для решения указанных выше задач. Существует единственная проблема — каждое вычисление может быть очень трудоемким.

Алгоритм уточняющего прерывания. Если имитационная система позволяет передавать произвольные данные (сообщения) между двумя любыми субъектами в имитационной модели различными способами (сообщения передаются по именованным портам, снабженным очередями FIFO; сообщения снабжаются меткой времени; субъекты могут “засыпать” до прихода сообщения в какой-либо порт (DEVS-формализм [3, 4])) или создавать имитационные модели “управляющего уровня”, т. е. модели управляющей программы, которая активируется только при получении сообщений от рядовых субъектов модели с требованием на управление и выдает “управляющие команды” в виде сообщений, отправляемых одному или нескольким субъектам [1], то можно организовать исполнение модели, при котором:

• 1)    субъекты будут вычислять время следующего события, используя способ 1;

• 2)    в случае возникновения трудностей с вычислениями, предусмотренными способом 1 (например, невозможно вычислить весь путь), сигнал будет отправляться на управляющий уровень;

• 3)    управляющий уровень будет посылать сигнал “спящим” субъектам с указанием возможности возникновения опасной ситуации;

• 4)    “спящие” субъекты будут обязаны вновь вычислить время следующего события (столкновение машин произойдет раньше запланированного) или каким-либо другим образом изменить свое состояние (запустить еще несколько линий помимо уже работающих, чтобы подготовиться, например, к принятию ТБ шириной в несколько линий).

Такой способ обладает следующими преимуществами:

• 1.    Вычисление времени следующего события становится простым и наглядным.

• 2.    Раннее прерывание “спящего” субъекта позволяет дробить временной интервал. Такое дробление может быть неограниченно мелким, что, однако, не будет приводить к прекращению моделирования, поскольку в каждом случае вновь вычисленный временной интервал будет ненулевым. Такого эффекта нельзя достичь даже при моделировании с фиксированным шагом по времени (как правило, при таком подходе временной интервал выбирается таким образом, чтобы имитационное моделирование выполнялось с максимально возможной точностью за приемлемое время).

• 3.    Существующие алгоритмы. GPSS имеет средства приоритетного прерывания при появлении в очереди на обслуживание задачи с большим приоритетом (команда PREEMPT). В данном случае GPSS совершает еще и заданное действие — перемещает незаконченную заявку обратно в очередь или на другой, заранее определенный прибор.

В алгоритме уточняющего прерывания субъекты могут распоряжаться сигналом на прерывание по своему усмотрению и выполнять любые действия при получении такого сигнала (вплоть до его игнорирования). Именно поэтому автор считает, что данный алгоритм представляет собой новый подход к построению имитационных моделей.

Заключение. С использованием приведенного алгоритма создана библиотека имитационного моделирования конвейерной сети, описанной как задача 1. Разработка алгоритма была обусловлена необходимостью реализации системы имитационного моделирования и позволила построить правдоподобную имитационную модель с хорошим быстродействием. На рисунке приведен кадр работы такой модели с использованием простой топологии ЭМК. По ссылке доступна рабочая версия системы имитационного моделиро-

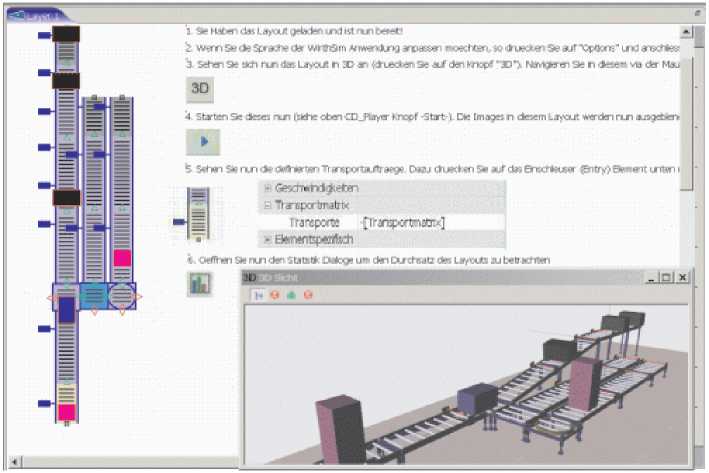
Имитационная модель в задаче 1

вания, работающая с применением данного алгоритма. Одно из достоинств этой системы — возможность совмещать подход системной динамики и алгоритма уточняющего прерывания.