Алгоритм Верле для многопроцессорных систем

Компьютерное моделирование в современной физике решает ряд задач, которые непосильно разрешить постановкой натурного эксперимента. Современная физика описывает практически все закономерности макромира в нормальных условиях, а вести исследования в областях низких или высоких температур, давлений проблематично, т.к. нет такой аппаратуры, которая могла бы работать в таких условиях. Поэтому для решения ряда задач научное сообщество прибегает к численному эксперименту, который позволяет смоделировать с достаточной достоверностью физические процессы, протекающие в реальных системах и выявить необходимые закономерности [1].

Современные компьютеры обладают высокими вычислительными способностями, но для наиболее приближенного описания физических систем необходимо моделировать порядка 1023 частиц, что на данный момент времени выполнить невозможно. Использование алгоритмов параллельных вычислений позволяет существенно сократить время моделирования. Рассмотрим одну из возможностей адаптации алгоритма Верле моделирования методом молекулярной динамики (МД) под многопроцессорные вычислительные системы.

Метод молекулярной динамики, попросту говоря, является численной реализацией решения уравнений движения Ньютона для множества частиц. Полную силу, действующую на i -й атом, можно представить в форме суммы векторов [2]

N - 1

^ =- Z VФ (ij ) .                              ⁽¹⁾

При этом предполагается, что известны координаты центров всех атомов и вид потенциала взаимодействия Ф ( r ). Энергия частиц инертного газа, например, может определяться потенциалом Леннарда-Джонса

Ф ( r ) = 4 - ([ T ]" -[ T ] ⁶ )

Если в некоторый момент времени t известны координаты и импульсы всех атомов, то с помощью уравне- ний Ньютона можно определить траекторию i-го атома на заданном промежутке времени. В случае отсутствия внешних полей его координата и скорость будут иметь вид

1 N - 1

qA t + A t ) = !) , ( t ) A t - ------£ V Ф (ij )( A t )² + q i ( t ) ,

2 m i j

1 N - 1

u , ( t + A t) = u , ( t) --^ VФ (ij ) A t .

m_i j

Возьмем для примера систему из N частиц инертного газа. Алгоритм Верле позволяет повысить точность итерации моделирования за счет частичного изменения скоростей частиц [3].

Для определения сил, действующих на одну частицу, необходимо определять расстояния до всех остальных N -1 частиц. Эта процедура дает наибольшую вычислительную нагрузку. В среде программирования MS Visual Studio имеется компонент Net.Framework BackgroundWorker, с помощью которого возможна организация вычислительных операций в асинхронном фоновом режиме.

Е.И. Герман, Ш.Б. Цыдыпов. Алгоритм верле для многопроцессорных систем

Массив координат частиц системы при расчете ускорений представляет собой массив переменных, здесь ускорение i -й частицы напрямую связано с положением любой другой j -й частицы, поэтому прямое разделение подпрограммы расчета ускорений на два и более асинхронных процесса фактически невозможно. Вместе с тем возможно использование одного управляющего компонента BackgroundWorker0 и двух счетных компонентов BackgroundWorker1 и BackgroundWorker2. Тогда схема разделения вычислительных операций одной итерации МД будет представлять следующую последовательность:

• 1.    BackgroundWorker0 обнуляет ускорения на начале текущей итерации, запускает BackgroundWorker1 и BackgroundWorker2 и ожидает событий завершения работы этих компонентов.

• 2.    С использованием компонента BackgroundWorker1 производится расчет ускорений по первым N /2 частицам системы, с использованием BackgroundWorker2 – по последним N /2 частицам.

• 3.    По завершении выполнения работы асинхронных потоков при помощи BackgroundWorker0 производится расчет ускорений, вызванных силами взаимодействия первых N /2 частиц и последних N /2 частиц.

Представленная схема использована для двухпроцессорной вычислительной системы. Теоретически прямой расчет ускорений для системы из тысячи частиц влечет за собой 499500 итераций цикла, при использовании предложенной схемы разделения вычислений на один процессор приходится 249500 итераций, что приводит к сокращению времени расчетов примерно в два раза. На практике увеличение скорости вычислений составляет порядка 60%, это связано со спецификой работы операционной системы и неравнозначностью вычислительных ядер процессора.

В качестве сравнительного показателя произведен расчет радиальных функций систем жидкого аргона при температуре 200 К и концентрации частиц 3•1028 м-3. Инициализация проводилась из упорядоченной расстанов- ки атомов в узлах кубической решетки.

Функция радиального распределения определяет плотность вероятности обнаружения частиц в сферическом слое dr на расстоянии r от заданной частицы, являющейся центром лабораторной системы координат [4]

g 2 ( r ) =

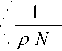
N

z i = 1

n i ( r , r + A r ) 4 n r ² A r

Ниже представлены графики радиальных функций распределения для молекулярных систем из 10000 час- тиц, полученные путем моделирования стандартным алгоритмом Верле и предложенным алгоритмом с параллельным разделением вычислительных потоков. В обоих случаях моделирование поводилось в течение 20 мин на одинаковых вычислительных системах.

Из рисунка видно, что в случае моделирования классическим алгоритмом Верле описанной системы, двадцати минут не достаточно, для того чтобы система пришла к равновесному состоянию, в вычислительном плане предложенный алгоритм гораздо продуктивнее.

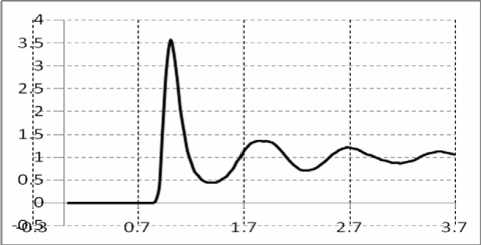
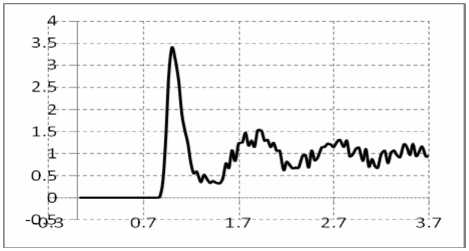
Рис. Радиальные функции распределения, полученные путем моделирования в течение 20 мин системы из 10000 атомов аргона, справа – предложенным алгоритмом, слева – классическим алгоритмом Верле

Предложенная схема применима и для вычислительных комплексов с большим количеством процессоров, для этого необходимо разделение вычислений на большее количество счетных потоков.