Алгоритм второго порядка точности по времени для решения уравнений Максвелла

В работе [1] излагается разностный метод решения уравнений Максвелла с применением разностной схемы “push-pull” первого порядка точности, которая позволяет исследовать градиентные волокна на малых расстояниях и дифракционные оптические элементы непосредственно за их плоскостью Разностный метод реализован для решения уравнений Максвелла в декартовых координатах в случае ТЕ поляризованной волны. В настоящей статье представлена разностная схема второго порядка точности по времени, которая позволяет сократить время расчетов за счет более крупного шага дискретизации. Проводится сравнительный анализ точности решения уравнений Максвелла.

1. Постановка задачи о распространении излучения

Суть постановки задачи, приведенной в работе 11] состоит в следующем: среда представляет собой тонкий слой, расположенный в плоскости (Y,Z), а излучение направлено вдоль оси Z. В случае ТЕ поляризованной волны уравнения Максвелла примул вид:

'ж, 1 (бн, бнА ---— = ----.----— i, ^ еД бг ^ )

6H_V Ж = ^:                      (1)

। от ос

| 6Н, _ Ж_л

I бс А'

где Е и И электрическая и магшгтная составляющие поля, т = ct с - скорость света в свободном прост- ранстве, t - время, s -диэлектрическая проницаемость. Полагаем, что на границе слоя £Л - 0.

• 2 . Синтез разностной схемы повышенного порядка точности

Будем решать систему (1) посредством конечных разностей. Для этого рассмотрим множества функций Ех (z, у, т\ И „ (z, у, т), Н, (z, у, т) в области оДй<г<^--^у<-,0<т<т\.

• 1             2 ^z 2 J

где L - длина прямоугольной области, d - ширина прямоугольной области,

Т =ctb tr длительность эксперимента.

Определим на ней сетку:

®Wr = fe» У J- Т_й) G у} где (z„ у_р т_Л) - узлы сетки, причем

О <  i < N_x - I;

• 1  <  j  <  N 2- 2;

0  <  n  <  N 3- 1 .

Шаги сетки определяются формулами:

Л L Л d'*Т

Аг =------; Ау =--; Дг =.

N.-V У N^-V N^-V'

Основываясь на общих принципах построения схем Писмена-Рэкфорда изложенных в [2], постро

A? ₊ С А _ 2 ____ n\z,y^²       I Ат n\z, y^²) ^X,J

At r-n-y. =             _ n4z,y^2           Ar x*'j

-    1    H”"^ +---1----//л^ + n2^z,y^ ^ n4z,y^

n1^, y^y Hs‘,J n2^z, y^y Illj"xf .

Дг _ L — - 2__—— k"*1 + m2(z, y)V ( Ar n4z, y)Ay2 J Xt''

, Ar -^ti ___2          , n^z, y)V x',nV Ar x,-,

,__U"__ИП _ n^z,y^ x,'f n2^z,y^

14п^У2 ,              и"*У1

n'^z, y^te >l4"x-'    n*(z, y)Az ^‘^

которые решаются методом прогонки.

В узлах (х,< yjf r^J при значениях индек сов:                          ,:.у

О <  i < N^y* i;

j = 1;

О <  п 5 N ₃ - 1

построим альтернативную систему аппроксимирующих уравнений

им неявную разностную схему. Запишем систему

разностных уравнений 0.5Ar      ^(z, y)		^-^ ^_-н:.,У
		Ле            Д? "if^-H"^ /^‘-Z^1^
J           O.SAr      n2	^/Й

0.5Ат    ^(^у)!

^-йУ2 1 [

0.5Дт    ^(^у)

Аг        ^

ррУг-урУт ^\ _jp

Аг

А/2-А/2 СУг-еУ1

Н^ -И?    £7’ - £7’

Система (2) аппроксимирует (1) в узлах (z,, уj, г_п) при значениях индексов:

О < i < N _х - 1;

Ет

^х-нх

Подставив третье уравнение системы (3) в первое и четвертое во второе, получим разностные уравнения

^Лт—-Е"^^г J  2- ^Лт + z? (z,y)Az^{2 J,}-^u ( Дг n²(z,y)Az²J ^

гГ^уУ^1

нп Ут +                  l n2(z,y)Az ,+UJ n2(z,y)Az V,J -------1/ Г "l         7Г n . ”2(z,y)Ay г'"'4 z?2(z,y)Ay ZlJ’

^" £^пЛ J. f 2 ^^T n\z, y)V ^,м^   ( Ar n^z, y)Ay²

n\z, y^Ay2 Ч)*' Ar n2(z, y)Ay  Z|,Ml    n2(z, y)Ay Ч n2(z, y)Az y"l•,    n\z, y)Az   y,,;

^4' 4

также решаемые методом прогонки.

Теперь, зная электрическое иоле, определим магнитное

н"*^ -у-.j я;> £"*ХА _ £,, + -^ ХМ Ат н:п - н*: Az £77 - Е7' Ат Ду при значениях индексов:

О < i < N, - 1;

2 <  j < N ₂ - 2;

О <  п < N₃ - 1

«7^ - н; е7'/2 - е7^

И Ar              Az j_j п+1 _ /у"                _ £и^

Ат             Ау при значениях индексов:

О < / < А , - 1;

У = |;

Возьмем в качестве краевого условия £т| = 0 и торцевого условия Е, = A^y^os^tot+лу^У где А - действительная амплитуда волны в скалярном приближении.

Схема (2), (3) аппроксимирует краевую задачу (I) с погрешностью аппроксимации О(Ат2,Аг,Ау). Это досчитается использованием обеих проекций поля Н при определении Еп'°" и Е"'1, чего не было в схеме “push-pull”.

Л Сравнение эффективности предложенной схемы и схемы “pusk-ри1Г

Проведем оценку относительной погрешности решения задачи расчета прохождения моды по вакуумному волноводу с металлическими стенками, представленной в [I]. Погрешность определим как

X

max

-•У

j?41^*^  ^ „ даналит.

даналит.

На рис. 1 представлены зависимости погрешностей от дискретизации по времени для схемы “push-pull” и схемы, представленной в настоящей статье. At=X/(fc)

Численные эксперименты проводились при следующих значениях параметров: t=10"^llc. d=3MKM, L=3mkm, Az=O.OO58mkm, Ау=0.023мкм, Х=1мкм, At=0.333-10‘¹², 0.166-10¹², 0.1 IMO"¹², 0.0833-10"¹², 0.0666-10'¹², 0.0556-10"'², 0.0476-10'¹². 0.0416-10"¹², 0.037-10’¹², 0.033 10'¹²c.

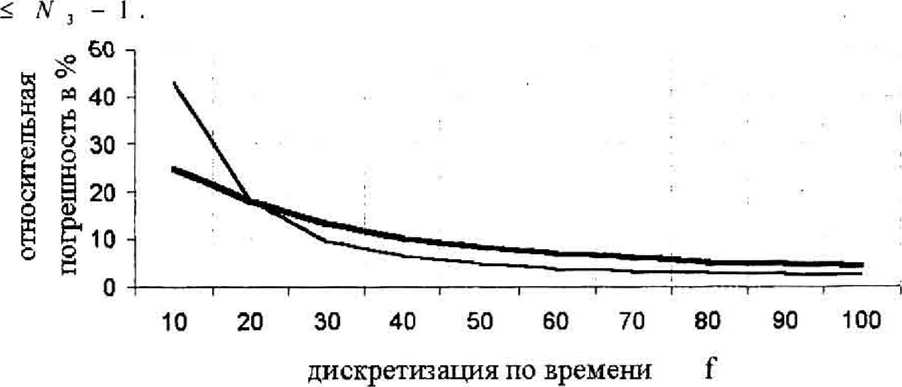
Рис. 1 Зависимость погрешностей от времени. Тонкая линия - погрешность решения с помощью схемы повышенной точности по времени, Толстая линия - погрешность решения с помощью схемы “push-pulP

Очевидно, при мелкости более, чем 20 отсчетов по времени, схема повышенного порядка точности является предпочтительной. Отметим, что на рис. 1 погрешность решения с помощью схемы повышенного порядка точности по времени имеет квадратичный характер зависимости от дискретизации по времени.

Заключение

В результате проведенного вышеизложенного численного эксперимента удалось установить, что в отличии от метода, описанного в [1], изложенный метод позволил практически в два раза повысить точность при сохранении временных затрат.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 96-15-96026)