Алгоритм выбора оптимальных границ интервалов разбиения значений признаков при классификации

Разбиение значений количественных показателей на интервалы широко применяется в различных алгоритмах анализа данных. В прикладной статистике значения количественных признаков, как правило, разбивается на заранее заданное число равных интервалов. Примером тому служит построение гистограмм, децильного и процентильного распределений.

Задача разбиения на интервалы рассматривалась и в теории распознавания образов с учителем. В [1] описан метод, реализация которого основывается на предположениях о законе распределения и числе интервалов. Метод является эвристическим, для разбиения на интервалы используется мера неопределённости принадлежности объекта к тому или иному классу энтропии, допускается отсутствие разбиения.

Использование численных методов оптимизации позволяет подбирать параметры модели, при которых алгоритмы распознавания допускают наименьшее число ошибок на заданной обучающей выборке. Метод, осуществляющий подгонку моделей распознавания и прогнозирования под выборку, получил название минимизации риска [2]. Увеличение сложности модели не всегда является благом, так как “оптимальные” алгоритмы начинают хорошо подстраиваться под конкретные данные, в том числе под измерения обучающей выборки и погрешность самой модели.

В теории искусственных нейронных сетей (ИНС) сложность модели распознавания выражается через способность к обобщению. Требуется, чтобы алгоритмы ИНС не только хорошо решали задачу на обучении, но и были способ- Згуральская Екатерина Николаевна, старший преподаватель кафедры «Самолетостроение».

ны также хорошо принимать решение на объектах, которые они не видели в процессе обучения. Этим целям служат разработки новых методов интеллектуального анализа данных, позволяющих получать новые знания о решаемой задаче и использовать их, в том числе, и для повышения точности алгоритмов ИНС [3] для произвольных допустимых объектов.

Задача разбиение на интервалы значений признаков классифицированных объектов в [3] сформулирована как детерминистическая. В основе критерия метода лежит проверка гипотезы “ Существует такое разбиение, при котором каждый интервал содержит все значения признака объектов одного класса ”. Очевидно, что при проверке число интервалов должно быть равно числу классов объектов.

Истинность, указанной выше гипотезы, означает, что между интервалами значений количественных признаков и классами объектов существуют взаимно-однозначное соответствие. На практике интерес представляет ответ на вопрос: Насколько истинны утверждения гипотезы на реальных данных? Универсальной и легко интерпретируемой мерой истинности служат значения в интервале [0,1] . Концы интервала [0,1] определяют оппозицию: значения признака неразличимы – значения признака различимы до уровня взаимно-однозначного соответствия интервалов и классов объектов.

Описываемый в работе алгоритм инвариантен к масштабам измерений, может быть использован при:

• -    поиске латентных (явно не измеримых) признаков в базах данных для моделирования процесса интуитивного принятия решений;

• -    преобразовании значений количественных признаков в номинальные с минимальной потерей информации;

• -    отборе информативных наборов разнотипных признаков.

Для уменьшения объёма вычислений предлагается проводить предобработку данных. Даётся оценка комбинаторной сложности алгоритма без использования предобработки и при её использовании.

1.    ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ

Рассматривается задача распознавания в стандартной постановке. Считается, что задано множество объектов E ₀ = { S _p..., S m } , содержащее представителей l непересекающихся классов K 1 ,..., K_; . Описание объектов производится с помощью набора из n разнотипных признаков X n = ( X 1 ,..., x n ) , 3 из которых измеряются в номинальной шкале, n — 3 в интервальной шкале. Считается, что задан критерий F ( * ) для разбиения значений количественного признака на непересекающиеся интервалы. Требуется определить значения границ l интервалов при F ( * ) ^ extr .

Обозначим через I , J множество номеров соответственно количественных и номинальных признаков в описании допустимых объектов, 1 1 + | J = П . Упорядоченное множество значений признака X j , j G I разобьём на непересека-ющиеся интервалы ( c ₂ k _{— 1}, c ₂ k ], c ₂ k _{— 1} <  c ₂ k , k = 1, 1 , каждый из которых считается градацией номинального признака.

Пусть u_i^p - множество значений признака x j , ^{j G 1} класса K_i в интервале ^{( c} 2 p — 1 , ^c 2 p ^], A = ( a ₀,..., a l ), a ₀ = 0, a l = m , a p ^— порядковый номер элемента упорядоченной по возрастанию последовательности r j 1 ,..., r jm значений X j из E 0 , определяющий правую границу интервала c _{2 p} = r a p .

Критерий ll

ZZ u p ( u p — 1) p = 1 i = 1

Z l K , i(| K , | — 1)

V i = 1                    J

( ^{1 1}

l

ZZ u p ( m — l K i l — Z u p + u p )

p = 1 i = 1

j = 1

i

Z l K i l( m — l K i l)

V           i = 1                                J

^ max _z . _x

{ A } ( 1)

позволяет вычислять оптимальные значения границ интервалов ^{{( c} 2 p — 1 , ^c 2 p ^]} и использовать их для определения градаций количественного признака в номинальной шкале измерений. Процесс преобразования при этом оказывается неразрывным от классификации, вводимой на множестве объектов обучения, и может быть реализован с учётом пропусков в данных.

Основные затраты вычислительных ресурсов при нахождении экстремума (1) приходится на вычисление {uf }. Максимальное число непересекающихся интервалов при разбиении упорядоченной последовательности rj 1,..., rjm при числе классов l равно

^ ( 1 , m ) =

f     2(m — 1), 1 = 2,

2 ( 1 — 1 )

2 H(m — 21 + k), 1 > 2.

, k = 3

Количество операций (сложность алгоритма) для подсчёта { u ip } определяется по среднему числу проверок условий вхождения значения признака в один из l интервалов (по две в интервале) и операции суммирования с 1

F ( 1 , m ) =

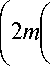
1 + 1 3

2 J

+ m

J

y(1, m) = m(2+1 )^(1, m).

Для уменьшения комбинаторной сложности вычислений предлагается воспользоваться предобработкой данных. Суть предобработки заключается в формированиии по упорядоченной последовательности rj 1,...,rjm целочисленной матрицы вида d10 d 1p.. d 1 m

D =

d d d

V^U 1 0^U 1 1 ". 1m J

в которой индекс столбца элемента dpi, p = 1,1, i = 1, m соответствует объекту S g E 0 со значением признака rji . Элементы матрицы (3) вычисляется как d pi

f 0, i = 0,

_ d p , , — 1 ⁺ g ⁽ p , i ), i > ^{0, где}

g ⁽ p , i ) =

' 1, ^{S G} K p , \ 0, S G K p .

Число представителей     u_t ^p класса

Kp, p = 1,1, t = 1,1 в интервале [c1, c2 ] при t = 1 и (c2t—1, c2t ] при t > 1, левые и правые границы которых соответствуют индексам п = at—1, V = at, c21—1 = r^ , c21 = r)V, определяется как utp = dpv — dpn . (4)

Сложность алгоритма вычисления { u p } ^по (3),(4) не превышает 1 ^ ( 1 , m ). Эта оценка сложности может быть понижена при наличи пропусков в данных и повторяющихся значений.

Благодаря использованию (4) по матрице (3) стало возможным вычисление (1) для интервалов и весов латентных (явно не измеримых) признаков. Под весом здесь понимается оптимальное значение критерия (1). Примерами латентных признаков может служить X i X j , X i X j , где X i , X j G X и i , j G I . На практике латентные признаки часто используются в форме различных

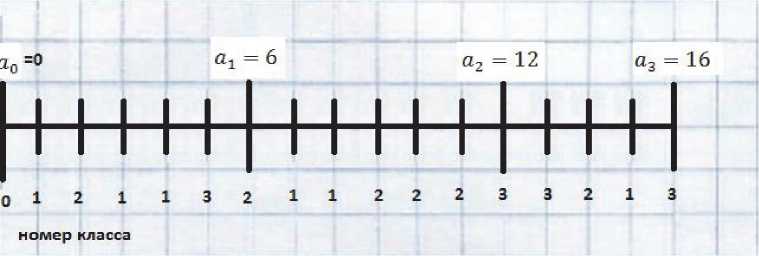
Рис. 1. Визуальная демонстрация алгоритма

индексов. Например, в медицине это индекс массы тела, индекс Кердо. Высокие значения весов латентных признаков (как правило, ближе или равные 1) служать основанием для построения моделей интуитивного принятия решений.

Вес признака по критерию (1) содержит в себе важную информацию об его информативности. Однако при отборе информативных наборов признаков нельзя полностью полагаться только на их упорядочение по значениям весов, то есть руководствоваться принципом “чем больше вес, тем признак более информативный в наборе”. В расчёт идёт и такой фактор как взаимная коррели-рованность признаков. Такая задача рассматривалась в [4], где исследовался вопрос отбора наборов информативных разнотипных признаков и их влияние на эффективность реализации искусственных нейронных сетей.

2.    ТЕСТОВЫЙ ПРИМЕР

Визуальная демонстрация алгоритма разби- ения на интервалы несовпадающих значений количественного признака по критерию (1) при m = 16, числе классов l =3 и мощности классов IK 11 = 6, K21 = 6, K3 | = 4 С использованием результатов предобработки (5) показана на рис. 1.

' 01123

D = 00111

_v 0 0 0 0 0

5555556 6 ' 34555666 1 1 1 2 3 3 3 4 _V

Согласно (2) максимальное число вариантов разбиения значений признака на интервалы ^(3,16)= 2X13X14 = 364 , сложность алгоритма без предобработки F(3,16) = 16x(2 + 3)x364 = 29520 с предобработкой (учитывая вычисление (3)) 3X 364 + 3X16 = 1140. Для варианта разбие- ния, указанного на рис. 1, получим u1=3, u2 =2, u3 =1, 12 =2, u2 =3, u2=1 U =1, u2=1, u3 =2 и значение критерия (1) равное 0,2146.

Другие возможные варианты разбиения на интервалы представлены в табл. 1.

Таблица 1. Варианты разбиения на интервалы

№ п/п	a 1	a 2	Значение критерия (1)
1	1	2	0,1944
2	2	8	0,3452(оптим.)
3	6	12	0,2146

Очевидно, что при оптимальном разбиении ( a 1 = 2 и a ₂ = 8 ) нет ни одного интервала, содержащего все значения признака объектов одного класса.

Номера интервалов оптимального разбиения по (1) можно рассматривать как градации при преобразовании значений количественного признака в номинальные. Такое преобразование использовалось для поиска информативных наборов разнотипных признаков с максимально выраженной независимостью в [4].

3.    ВЫВОДЫ

Численный алгоритм выбора оптимальных границ интервалов может быть использован при интеллектуальном анализе данных для преобразования количественных признаков в номинальные с минимальной потерей информации, при упорядочении разнотипных признаков по отношению сложности алгоритмов, выражаемой через способность корректно распознавать объекты фиксированной выборки с минимальной затратой вычислительных ресурсов.