Алгоритм выбора рациональных параметров крыла с учетом аэродинамической и весовой эффективности

требованиями, и значения удельной нагрузки на крыло, определяемого требованиями по обеспечению взлета, посадки и крейсерского режима полета, в качестве функции цели может быть принята взлетная масса самолета.

Методы исследования. Для расчета аэродинамического качества крыла удобно использовать метод дискретных вихрей (МДВ) [4]. Для оценки относительной массы конструкции крыла m кр воспользуемся новым универсальным методом весового анализа и оптимизации силовых конструкций, основанным на использовании модели тела переменной плотности (ТПП). Подробно суть метода изложена в [5]. Основная идея метода заключается в проведении итерационной процедуры оптимизации распределения плотности материала, вписанного в геометрические ограничения крыла. Критерием оптимальности в этом алгоритме является коэффициент силового фактора

C = G G=∫σэкв⋅dV

^K P ⋅ L , V (1)

где Р – характерная нагрузка, L – характерный размер, G – силовой фактор, σ экв – эвивалент-ное напряжение, V – объем материала конструкции.

Относительная масса конструкции крыла может быть определена по формуле:

m _кр = ϕ ⋅ n _р ⋅

^{[ а ]},   (2)

где ф - коэффициент полной массы, который выражает отношение полной массы конструкции крыла к массе силового материала, n p -расчетная перегрузка, S - площадь крыла, [ ^ ] - удельная прочность материала. Безразмерный коэффициент силового фактора позволяет построить следующий алгоритм оптимизации геометрических параметров крыла по критерию минимума взлетной массы самолета (рис. 1):

• 1.    После задания исходных данных (блок 1 на рис. 1) выбираются проектные переменные (блок 2) и им присваиваются конкретные значения (блок 3).

• 2.    Из условия постоянства удельной нагрузки на крыло рассчитывается значение площади (блок 4) и абсолютных размеров крыла (блок 5). Строится аэродинамическая модель крыла (блок 6). С использованием МДВ вычисляются аэродинамические характеристики самолета (блок 7) и относительная масса топлива (блок 8).

• 3.    Строится КЭМ крыла на основе тела переменной плотности (блок 9). Производится оптимизация и рассчитывается значение относительной массы конструкции крыла (блоки 10-12).

• 4.    На основе значений относительных масс топлива и конструкции крыла по уравнению существования определяется значение взлетной массы самолета (блок 13). Проверяется условие сходимости (блок 14). При неудовлетворении этого условия блоки 4-13 повторяются, при удовлетворении - происходит выбор новых значений проектных переменных (блок 3).

В результате для выбранных значений проектных переменных за счет оптимизации распределения плотности в КЭМ крыла достигается минимальное значение массы конструкции крыла и определяется соответствующая ему взлетная масса самолета. Далее тем или иным способом производится оптимизация проектных переменных. В данной работе для простоты и наглядности использовался перебор вариантов.

Результаты. Для отработки и тестирования алгоритма применим его к типовой задаче выбора удлинения X и сужения п нестреловидного трапециевидного крыла. Абсолютные геометрические размеры крыла в плане могут быть выражены через удлинение X , сужение п и площадь S . Относительную толщину профиля примем постоянной и равной с =0,12.

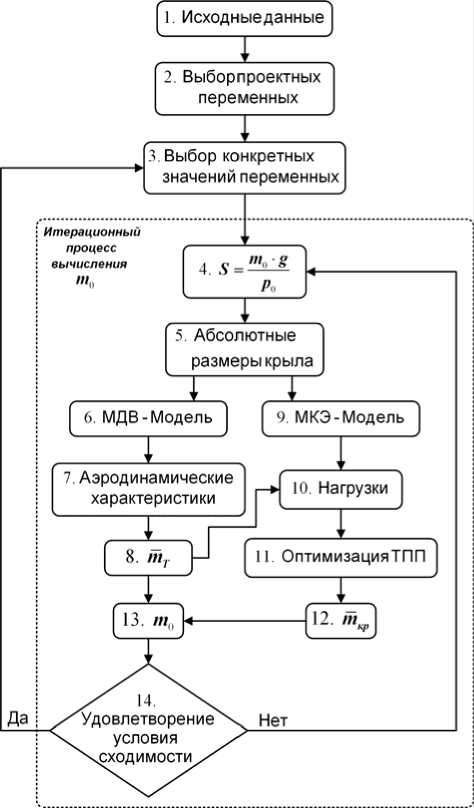
Рис. 1. Алгоритм выбора рациональных параметров крыла

Изменение значений проектных переменных будем производить по следующим наборам дискретных значений: Х=[4;6;8;9,6;12], п=[1;2,2;3]. В качестве исходных значений массы целевой и служебной нагрузок, удельной нагрузки на крыло, удельного расхода топлива и др. примем характеристики, близкие к характеристикам одного реального самолета: масса целевой нагрузки т ком =25200 кг, масса служебной нагрузки т_сл =2815 кг, удельная нагрузка на крыло р₀ =590 ДаН/м², удельный расход топлива на крейсерском режиме с_ркрейс =0,6 кг/ДаН.ч.

Рассмотрим применение алгоритма для двух значений дальности полета самолета: L=3500 км и L=7000 км. На рис. 2 представлена зависимость взлетной массы самолета от удлинения и сужения крыла и от дальности полета. Из представленных данных видно, что для каждого значения сужения крыла зависимость взлетной массы от удлинения имеет минимум. Это объясняется уже упоминавшимся противоположным влиянием удлине- ния на аэродинамические и весовые характеристики крыла и самолета в целом. Для самолета с дальностью L=3500 км минимальное значение взлетной массы m0=85824 кг достигается при значении проектных переменных η=3,0 и λ=6,0. Для самолета с L=7000 км минимальное значение взлетной массы m0=154099 кг достигается при значении η=3,0 и λ=9,6. Увеличение рационального значения удлинения при увеличении дальности полета является ожидаемым результатом и свидетельствует о работоспособности алгоритма.

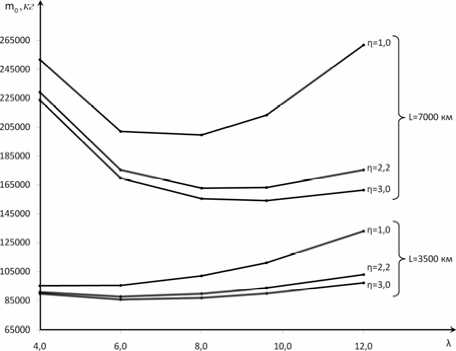
Рис. 2. Зависимость взлетной массы самолета от удлинения, сужения крыла и дальности полета

Выводы: использование для вычисления массы конструкции МКЭ, а для определения аэродинамических характеристик – МДВ не накладывает существенных ограничений на форму крыла и позволяет осуществлять обоснованный выбор параметров крыла нетрадиционной формы на ранних стадиях проектирования. Более подробно описанный алгоритм и его применение для крыла необычной формы рассмотрено в работе [6].