Алгоритм выбора среднего (mean shift) для обработки изображений

В качестве алгоритма сегментации был выбран алгоритм сдвига среднего (mean shift) предложенный Фукуна-гой и Хостлером в работе [1]. преимуществом этого метода является то что для его работы не требуется никаких дополнительных знаний о изображении и знания количества кластеров. Суть метода заключается в том, что задается функция оценки плотности распределения точек в пространстве признаков. Далее для этих точек строится градиент ядра оценки плотности распределения и вычисляется вектор среднего сдвига, задаваемый как вектор наибольшего увеличения градиента.

Сдвиг среднего всегда направлен по максимуму возрастания эмпирической плотности вероятности. Последнее обстоятельство гарантирует сходимость этой оценки в точку с нулевой производной. Из этого следует, что метод сдвига среднего – это метод адаптивного спуска по градиенту.

Результатом процедуры mean shift является новое положение в цвето-координатном пространстве для каждой точки. В общем случае этот результат ещё нельзя считать законченной сегментацией, так как не получены замкнутые области. Для того чтобы завершить процесс сегментации, необходимо объединить полученные в результате среднего сдвига точки в однородные области. Методика mean-shift во многих случаях приводит к созданию обла- стей точек, которые не могут быть отнесены к какой-либо крупной области. Фактически, это приводит к созданию большого количества мелких областей на границах различных объектов. Кроме этого, источником таких областей могут являться дефекты и артефакты на изображении.

Самым простым решением этой проблемы является расформирование областей, имеющих размер меньше определённого порога, и присоединение её точек к ближайшей крупной области. Альтернативным способом поглощения регионов является расформирование области в пользу того соседа, у которого ближе точка сходимости кластеризации методом mean shift.

Процедура mean shift является сложной процедурой, требующей большого объёма вычислений. Самой затратной частью является вычисление вектора среднего сдвига для конкретной точки. Для уменьшения времени, затрачиваемого на процедуру в целом, можно вычислять вектор среднего сдвига не для всех точек. Идея сокращения объёма вычислений основывается на том, что близко лежащие точки в пространстве признаков с большой вероятностью приходят к одному центру сходимости [2]. Другими словами мы можем выбрать некоторое окно h, меньшее окна h , и, вычислив центр сходимости для некоторой точки, назначить этот же центр сходимости для всех точек, лежащих

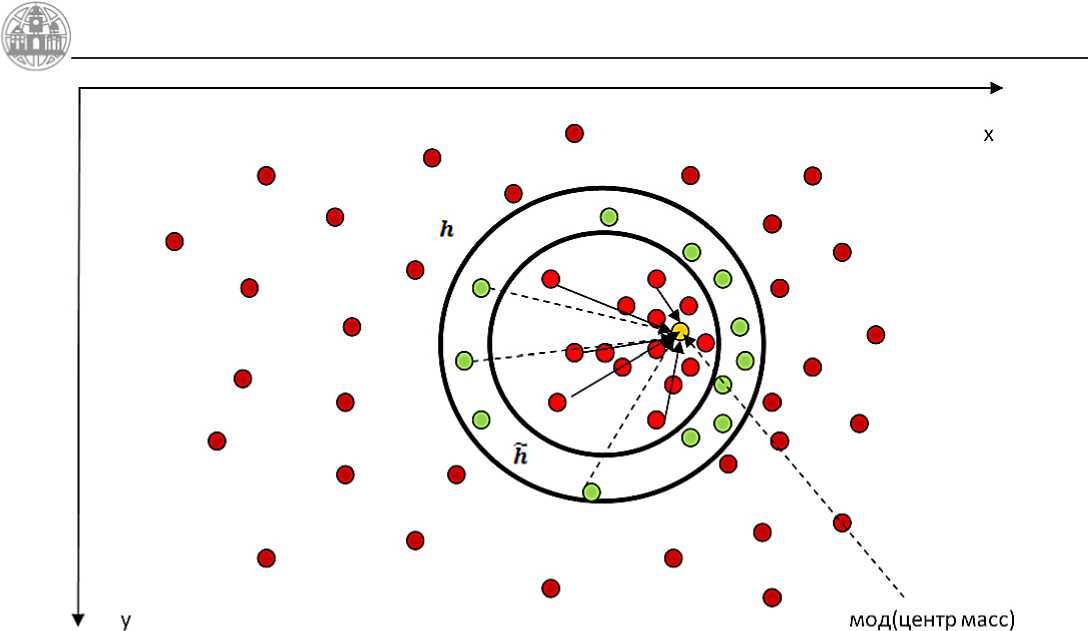
Рис.1. Графическое представление работы ускоренного алгоритма сдвига среднего.

в окрестности h от выбранной точки, и тем самым избежать повторных вычислений (рис. 1). Выигрыш в скорости зависит от величины параметра h. Однако подобные предположения приводят к ухудшению качества сегментации (возрастание вероятности ошибки).

Кроме того, вычисление вектора mean shift происходит для каждой точки независимо. Это означает, что процедуру mean shift для каждой точки можно выполнять параллельно, без необходимости синхронизации до этапа объединения точек. Сам процесс объединения точек не обладает значительной вычислительной сложностью, поэтому использование параллельных вычислений может повысить скорость работы метода в несколько раз.

Как уже было рассмотрено выше, метод mean-shift обладает следующими достоинствами: масштабируемость (время работы линейно зависит от количества обрабатываемых точек), робастность (процедура даёт устойчивые результаты при изменении входных параметров) и возможность параллельной обработки. Тем не менее, метод обладает следующими, еще не рассмотренными нами, недостатками:

• 1.    Необходимо выбирать размер окна h при настройке алгоритма на работу с конкретными данными, при этом часто для каждой координаты выбирается собственный размер окна, что так же усложняет настройку процедуры.

• 2.    При увеличении размеров окна резко возрастает время работы алгоритма.

  

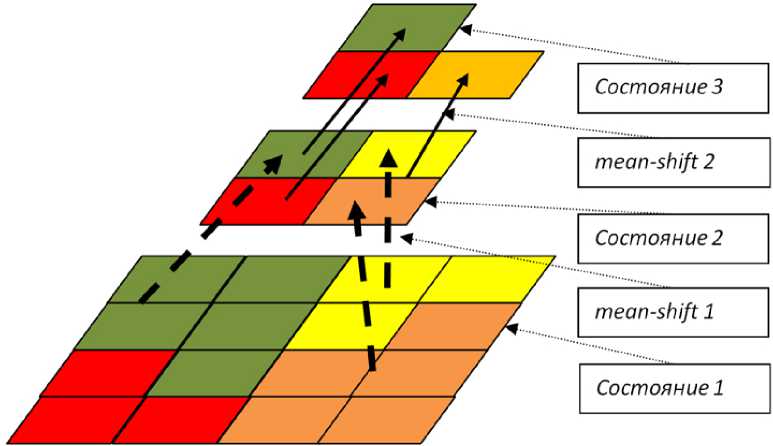
  Рис. 2 . Механизм агломеративной кластеризации.

  
  

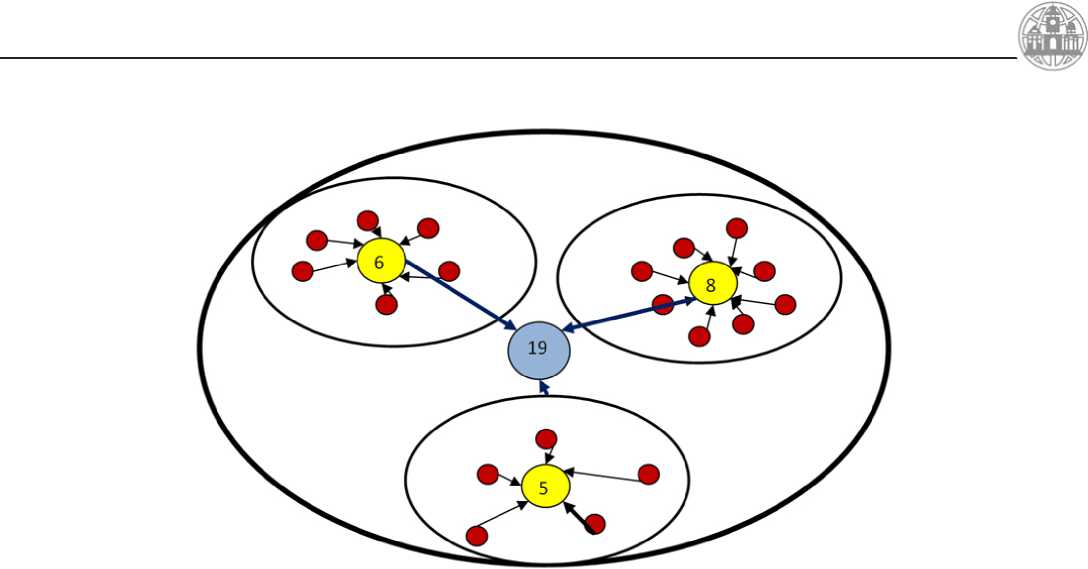
Рис. 3. Схема объединения кластеров.

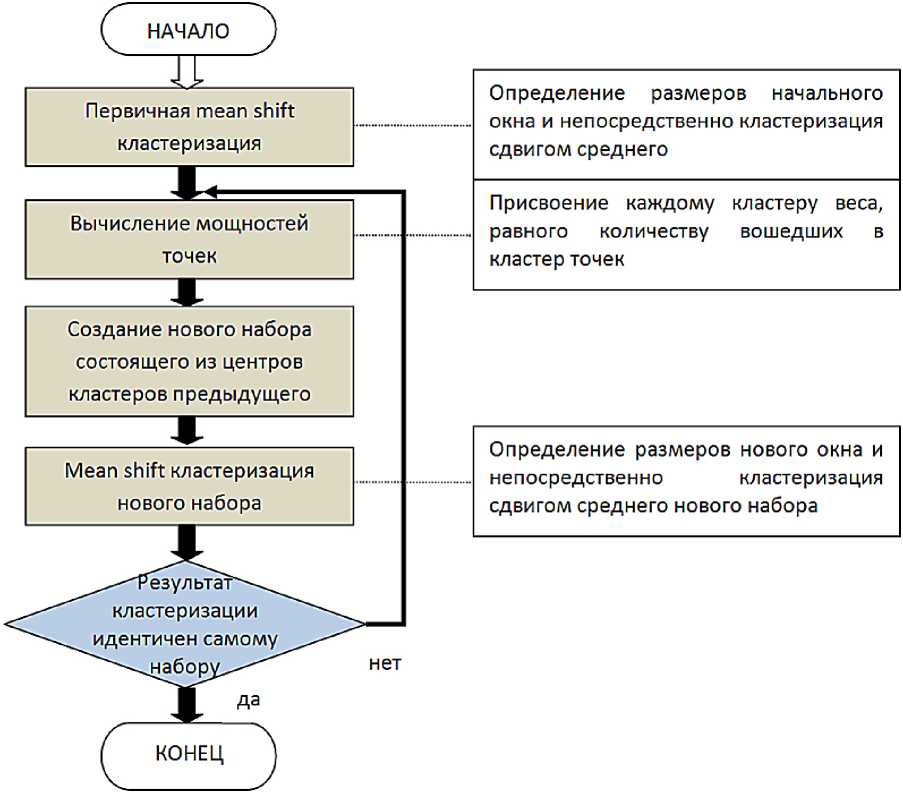
Рис.4. Блок-схема модифицированного алгоритма сдвига среднего.

Последний пункт имеет особое значение в виду того, что размер окна влияет на количество получаемых в результате кластеризации областей, причём, чем больше размер окна, тем меньше кластеров будет получено, а именно небольшое количество кластеров, как правило, является целью кластеризации.

Существует две естественных стратегии кластеризации: раздельная и агломеративная [3]. В данной статье, в силу описанных выше свойств алгоритма mean-shift, будет использована агломеративная стратегия (иерархическая), иначе говоря, сегментация будет проходить в несколько этапов.

На рис. 2 представлена общая схема агломеративной кластеризации: каждый следующий этап кластеризации работает с набором точек, состоящим из центров кластеров предыдущего этапа.

При использовании такой стратегии выполняется несколько процедур сдвига среднего, а значит необходимо для каждой из них подбирать размер окна h . Кроме того, этот размер должен постоянно увеличиваться. Для этого мы воспользуемся алгоритмом, предложенным в работе [2].

Предложенный в данной работе метод состоит в ограничении всего набора точек гиперпараллелепипедом с объёмом V и разбиению его на n субпараллелепипедов с объёмом:

V

^m -^- (54)

где n количество точек. То есть, если все точки были бы распределены по пространству равномерно, то каждая находилась бы в своём гиперпараллелепипеде с объёмом V_m , Соответственно, стороны гиперпараллелепипеда и будут определять размеры окна, то есть параметр h . Иными словами размер окна для i -го измерения будет определяться по формуле:

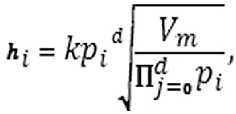
где p_i – коэффициент компоненты, определяется пропорционально сторонам основного гиперпараллелепипеда, d – размерность пространства, k – коэффициент, вводимый для того, чтобы иметь возможность управлять количеством формируемых кластеров.

По мере уменьшения количества точек, вследствие кластеризации, размеры окна будут расти, является необходимым условием для реализации агломеративной стратегии.

Кластеры, собравшие больше точек на определённом этапе, должны иметь преимущество на следующем этапе, для этого вводится понятие «веса точки», которая выступает сомножителем в арифметических операциях. «Вес точки» вычисляется исходя из количества точек первого уровня, собранных в кластере, центром которого является текущая рассматриваемая точка. Это проиллюстрировано на рис.3. На первом этапе кластеризации выделяется три кластера. Следующий этап работает уже с 3-мя точками, Эти точки неравноправны, больший вес имеет та, в которую пришло больше точек. Соответственно, на следующем этапе все три точки были объединены в одну, с суммарным «весом», равным девятнадцати.

Обобщая вышесказанное, представим алгоритм в виде блок-схемы на рис. 4: на первом этапе производится стандартная кластеризация методом mean shift с небольшим размером окна; затем вычисляется мощность каждой точки, являющейся центром кластера, и из этих точек формируется новый набор; затем производится кластеризация стандартным методом mean shift полученного набора. Последние три этапа повторяются до тех пор, пока кластеры не перестанут объединяться.