Алгоритм вычисления граничного ранга двоичной матрицы

1.    Модель решетчатых ошибок

Рассмотрим процесс передачи дискретных сообщений от источника, информации к получателю, который осуществляется по нескольким параллельным каналам. Каждый из каналов использует двоичные сигналы для передачи. Пусть количество каналов равно пу, длительность передачи по каждому из каналов равна n_t. Тогда входные и выходные сигналы можно отождествить с матрицами (A ij ), г = 1, ...,п у ; j = 1, ...,n_t, где г означает номер канала, j означает номер временного питщ>ва.та. Значения элементов равны 1 или 0.

В процессе передачи сообщений возникают различные специфические ошибки.

Когда, действуют замирания сигнала, импульсные и узкополосные помехи, ошибки могут возникнуть в нескольких столбцах и нескольких строках матрицы. В таком случае ошибки называются решетчатыим.

Пусть задано множество матриц (vi, V2,..., р м ) ^на входе канала. Пусть передается мат-

рица р^ а на выходе получена матрица у = р і + е	, где е - матрица ошибок.
Пример. Матрица.
/0 0 0	1 °\
1 0 0	1 0
е =110	01
0 0 0	0 0
100	00

«Московский физико-технический институт (национальный исследовательский университет)», 2019

есть ошибка решетчатой конфигурации с граничным рангом 3, так как искаженные символы сосредоточены в третьей строке и первом и четвертом столбцах.

Желательно правильно восстанавливать сообщение, если граничный ранг матрицы ошибок е не превосходит заранее заданной величины t. Нужен алгоритм вычисления граничного ранга двоичной матрицы.

2.    Пространство квадратных двоичных матриц над конечным полем

Пусть GF(2) - конечное поле, состоящее из q = 2 элементов. Пусть GF(2п) - расширение поля GF(2) степени п, п - натуральное число. Поле GF(2) будем назвать базовым полем, поле GF(2п) - расширенным полем.

Линейное пространство матриц А над

GF (2)

п х п

полем GF (2) с раем юрами п х п обозначается

А =	« 0,0 «1,0 • • •	«0,1      . «1,1      . •                         .	.    «0,п-1 .    «1,п-1 •	, « г,	У G GF (2)
	_ «п-1,0	«п-1,1   .	. « п - 1,п-1_

Ранг матрицы Rk(X) определяется как максимальное число линейно независимых над GF (2) строк (или столбце в). Граничный ранг р(А) двоичной матрицы определяется как минимальное число линий (строк и столбцов), в которых содержатся все ненулевые элементы матрицы [1+2].

Функция р(А) удовлетворяет всем аксиомам нормы [1]:

р(А) = 0 о А =

.

. .

.

*

.

.

*

.

.

*

.

.

. .

.

р(А) >  0 о А = 0.

^|р(А) - ^{р ( в} )| < ^р(А + ^в) < ^р(А) + ^{р (} ву

Гранично-ранговое расстояние. Примеры

Пример. Граничный ранг матрицы

1 1 1

равен 1, граничный ранг матрицы

/1 0 0\ равен 2, граничный ранг матрицы

/1 1 1\ равен 3.

Расстоянием между двумя матрицами А и В одинаковых размеров называется граничный ранг их разности:

<А,В)= р(А - В).                             (1)

Гранично-ранговое расстояние имеет все свойства обычного расстояния:

• 1)    d(A,B') = 0 о A = В.

• 2)    d(A, С ) + d(C, В ) >  d(A, В) - неравенство треугольника.

• 3)    d(B, A) = d(A, В) - свойство симметричности.

Первое и третье свойства получены из отмеченного выше соотношения

d(A, В) = p(A — В) = p(B — А).

Аналогично

d(A,C ) + d(C, В) =

= p(A — С ) + p(C — В) >  p((A — С ) + (С — В )) =

= p(A — В ) = d(A — В)

Таким образом, второе свойство расстояния доказано.

Гранично-ранговый код У G GF (2)ⁿ-f ^{x n t} - это любое подмножество пространства прямоугольных матриц с гранично-ранговой нормой.

Кодовое расстояние равно, по определению, минимальному из попарных расстояний между элементами кода [3]:

d = min p(v_t — V j ). t=j

Очевидно, для любого кода d < D = min(ny, nt).

4.    Алгоритм вычисления граничного ранга двоичной матрицы

Этот алгоритм был предложен автором в 2018 г. Основная идея алгоритма заключается в том, что на основе сравнения между векторами сумм столбцов и векторами сумм строк можно вычислить максимальное значение элементов. Цель определения максимального значения элементов - управление процессом вычисления граничного ранга, то есть граничным рангом является минимальное число строк и столбцов, в которых содержатся все единицы матрицы.

Вход: А = (A tj ) - двоичная матрица. с размером m х n

Выход: norm = p(A) - граничный ранг двоичной матрицы.

• 1)    У ^ 0.

• 2)    Вычисление векторов colnm =      (colnm[1], colnm[2],... , colnm[n])    и

• Une = (line[1], line[2],..., line[m]). colnm[j] - это сумм а элементов j-m столона матрицы, line[i] - это сумм а элементов i-й строки матрицы:

m colnm[j] = ^2 Ajj j = 1,...,n, г=1 n line[i] = У2 Atj i = 1,... ,m.

j=i

3)    Вычисление max _col_var - максимальное значение элементов в векторе colnm, max _col_index - индекс максимального 'значения элементов в векторе colnm. 4)    max _line_var - максимальное значение элементов вектора, line, max _line_index -индекс максимального значения элементов в векторе line. 5)    While max _line_var > 0 do 6)    у ^ у + 1. 7)    If max _col_uar > max _line_var then Д,тах co[ index ^ 0, г де i = 1.. .m. 8)    Else Mmax _ Une _index,j ^ 0; Г Д6 j — 1 ...Tt. 9)    Вычисление векторов colum и line. 10)    Вычисление max _col_var, max _col_index. 11)    Вычисление max _line_var, max _line_index. 12)    end while. 13)    norm — p(M) - минимальное значение из трёх значений у, m и п.

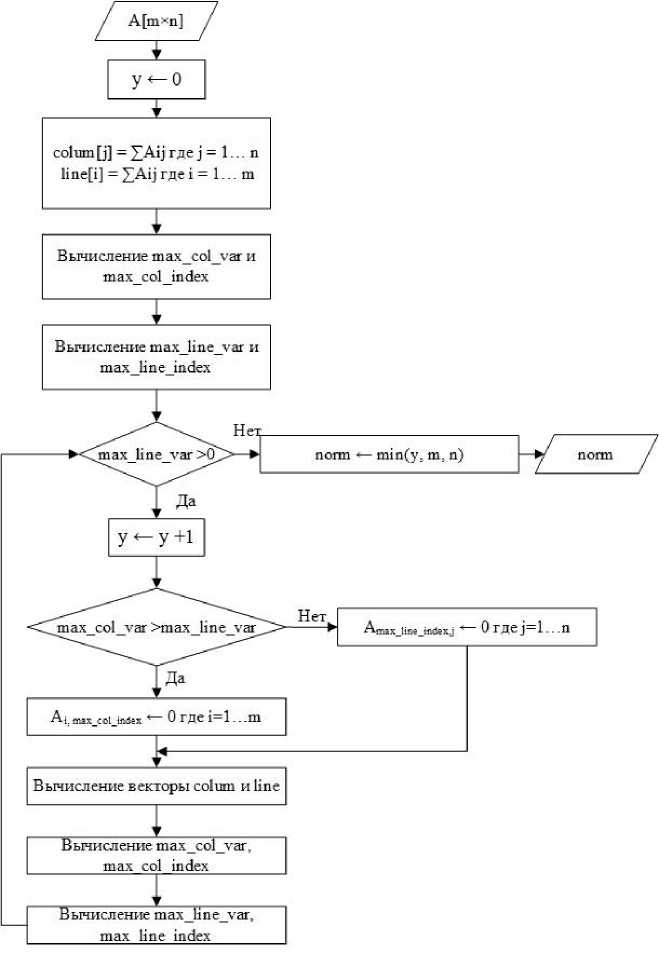
Рис. 1. Блок-схема, алгоритма, вычисления граничного ранга, двоичной матрицы

Доказательство. Пусть А - двоичная матрица размером m х п. Пусть у - количество разложенных матриц из А. Разложение матрицы А осуществляется в следующем порядке:

А = Ai + Bi, где Ai - двоичная матрица, у которой только одна строка (или столбец), в которой содержатся максимальное количество единиц из всех строк (или столбцов) матрицы А.

Пример

/1 0 0\    /10 0\   /0 0 0\

1  1  0  =  1 0  0  +  0  1  0  = A i + B1.

001  000  001

Аналогично для Bi: Bi = А2 + B2 и так далее.

В общем случае процесс разложения матрицы имеет следующий вид:

A = Ai + Bi,

Bi = A2 + B2,

^B y — i — ^A y .

Таким образом, на конечном этапе получим A = Ai + A2 + ... + Ау.

С учетом третьей аксиомы получаем

p(A) < p(Ai) + p(A2^ + ••• + p(A_y ) = 1 + 1 + ••• + 1 = у.

Матрицы А г не зависят друг от друга. Поэтому если значение у больше, чем ттг или п, то граничный ранг матрицы А равен min(m, п). В противном случае, как легко увидеть, граничный ранг матрицы А равен у.

5. Пример. Код (3,1,3). Дуальный код (3, 2, 2)

Пусть задан код (р, k,d), где р = 3 размер квадратной матрицы, к = р — 2 = 1-число информационных векторов (ж, у, 2), d = 3 кодовое гранично-ранговое расстояние. Матрицей кода (3,1,3) является бинарная матрица размера 3 х 3. Код (3,1,3) имеет вид

Пусть задано целое число элементов

ж у 2 2 ж у , у 2 ж множества L = 23 = 8.

	000    100    010    001
G 0 =	0 0 0  , Gi =  0 10  , G2 =  0 0 1  , G3 =  10 0 000    001    100    010 /1 1 0\        /10 1\        /0 1 1\        /11 1'
G4 =	0 11 , G5 = 110 , G6 = 10 1 , G7 = 111 101    011    110    111

Легко заметить, что p(Go) = 0 и р(С_г ) = 3, г де г = 1... 7.

Рассматривается разность двух матриц G — G j | € G. Поэтому гранично-ранговое расстояние равно 3.

Опишем данный код через G’ матрицу дуального кода (3,2,2) из матрицы G. В резуль тате получим

( ж

У

У ж

2\     / о(ж)

У I v I     d(2)

ж        Ь(у) + Һ(у)

Ь ⁽ У)

9(ж)

сД) + d(2)

Ф)  \

Цу)    I

а(ж) + 9(ж)

v

	/ а	b	с
v G =	d	9	Һ
	b + Һ	с + d	а + 9.

Дуальный кон (3, 2, 2) имеет гранично-ранговое расстояние 2.

6.    Код (р,р — 2, 3). Пример. Код (4, 2, 3)

Код (р,р — 2, 3) характеризуется параметрами (р, к, d) г де р - размер квадратной матрицы, к = р — 2 - число информационных векторов (ж_г, У г , Z,..., к_г, е_г), г де г = 0,... ,р — 1, d = р — к + 1 = 3 кодовое гранично-ранговое расстояние.

Для построения кода (р,р — 2, 3) сначала определить сопровождающую матрицу F_n. Пусть / (ж) = ж”+/_п-іж^п—і+• • •Т/іж+Уо - примитивный многочлен пан полем GF (2). Тогда сопровождающая матрица F_n имеет вид

010 ... 0  0\

001 ... 00

:      :     ...     01

\ /0 /1  

Порождающая матрица кода имеет общую формулу:

ж0 + ж1 + • • • + жп-3\

G =

^ж 0 ^F п ^{+ ж}і ^F,2 ⁺ • • • ^{+ ж} п - з ^ ” ²

жоҒ” 1 +жіҒ2(п 1) +-----+ж„

Р (п-1)(п-2) 3^Ғп         /

Здесь выберем сопровождающую матрицу Ғ_п так, чтобы p(G) > 3. В этом случае код (р, р — 2, 3) является линейным. Поэтому гранично-ранговое расстояние d(G i — G j ) > 3.

Кон (4, 2, 3) характеризуется параметрами (р, к,d). г,ле р = 4 - размер квадратной матрицы. к = р — 2 = 2- число шіформсгщюшіых векторов (ж, y). d = р — к + 1 = 3 кодовое гранично-ранговое расстояние. Символы векторов представляют собой элементы поля GF (2). Пусть G - (4 х 4)-матрица, которая состоит из информационных векторов. Матрица G имеет две информационные диагонали и две проверочные диагонали.

Код задается следующей порождающей матрицей:

G =

x y xF4 + yF2 xF2 + yF4

где x = (ж₀ ж_і ж₂ ж_з), y = (y₀ y 1 y ₂ y₃) - информационные вектор-строкіі длины 4. Здесь выберем сопровождающую матрицу F4 так, чтобы p(G) > 3. А матрица F4 - сопровождающая матрица многочлена ж⁴ + ж + 1:

		F 4 =			0 0 0 1	100 010 001 100
			( °	1	0	0^					(0	0	1	0\
x F 4	+ y F 2	= (ж0 жі ж2 жз)	0 0	0 0	1 0	0 1	+ (У0		Уі	У2 Уз)	0 1	0 1	0 0	1 0
			1	1	0	0					0	1	1	0
		= (жз + У2 ж0 + жз + У2 + Уз жі + У0 + Уз ж2 + Уі),
			(0	0	1	0^					(1	1	0	0\
x F 2	+ y F 4	= (ж0 жі ж2 жз)	0 1	0 1	0 0	1 0	+ (У0		Уі	У 2 Уз)	0 0	1 0	1 1	0 1
			0	1	1	0					1	1	0	1

= ($2 + У 0 + У 3 $2 + $3 + У 0 + У 1 + У 3 $0 + $3 + У 1 + У 2 $ 1 + У 2 + У з ).

Таким образом, получена общая формула:

$0                  $1

У0                    У1

$3 + У2      $0 + $3 + У 2 + У3

$2$3

У2У3

$1 + У0 + Уз       $2 + У1.

.$2 + У0 + У3 $2 + $3 + У0 + У1 + У3 $0 + $3 + У1 + У2 $1 + У2 + У3_

Пусть задано целое число матриц множества L = 28 = 256. С помощью компьютера результат получен (табл. 1).

Таблица!

Результат вычисления граничных рангов всех кодовых матриц G

Граничный ранг p(G)	0	1	2	3	4
Количество матриц	1	0	0	101	154

Из таблицы результата получено гранично-ранговое расстояние d(Gi — Gj ) > 3.

7.    Заключение

Представленный в статье алгоритм является новым. Алгоритм вычисления граничного ранга является основным результатом данной статьи, и с помощью этого алгоритма решалась задача построения кодов с расстоянием 3. Результат построения данных кодов представляет собой основу для решения последующих задач оптимальных кодов, исправляющих одиночные гранично-ранговые ошибки.

Автор выражает благодарность профессору Э.М. Габидулину и д.т.н Н.П. Пилипчук за замечания, которые способствовали улучшению статьи.