Алгоритм выделения интенсивных аномальных изменений во временном ходе параметров ионосферы

Работа направлена на создание математических моделей и алгоритмов анализа природных временных рядов сложной структуры. В статье рассматривается задача, связанная с анализом параметров ионосферы и выделением аномальных изменений, характеризующих возникновение ионосферных неоднородностей (ионосферных бурь). Реакция ионосферы на изменения в околоземном космическом пространстве (солнечные вспышки, корональные выбросы, геомагнитные бури и суббури) проявляется в виде резкого повышения (понижения) электронной концентрации, которое приводит к возникновению ионосферных бурь [1–4]. В периоды ионосферных бурь в ионосфере возникают аномальные процессы, приводящие как к значительным изменениям временного хода данных, так и к внезапным локальным изменениям различной формы и длительности. Ионосферные бури могут включать «положительную» и «отрицательную» фазы, имеющие сложное пространственновременное распределение, и их характеристики зависят от географического положения (полярная и авроральная зоны, среднеширотные и экваториальные области), начала геомагнитной бури, местного времени и др. [1–4]. Возмущения вызывают нарушения в распространении радиоволн в КВ-диапазоне (например, рассеивание радиоволн на ионосферных неоднородностях), а также в работе современных наземных и космических технических средств [1, 3, 5], поэтому их своевременное обнаружение имеет важное прикладное значение. Мониторинг состояния ионосферы основан на анализе регистрируемых параметров среды (критическая частота (foF2), полное электронное содержание (ПЭС) и др.). Анализ данных foF2 и обна- ружение аномальных изменений является предметом данного исследования. Данные критической частоты F2-слоя ионосферы (foF2) регистрируются методом вертикального зондирования с помощью цифрового ионозонда и после первичной обработки представляются в виде временных рядов. Регистрацию данных foF2 выполняет ИКИР ДВО РАН, п-ов Камчатка. Регистрируемые временные ряды foF2 имеют сложную нестационарную структуру, включающую регулярные вариации, определяемые солнечной активностью и локальными факторами, а также аномальные изменения разномасштабной структуры, характеризующие возникновение ионосферных неоднородностей [6–9].

Учитывая сложную структуру регистрируемых данных foF 2, применение традиционных методов, основанных на медианном сглаживании, позволяет изучать наиболее устойчивые характеристики ионосферного процесса, но приводит к потере информации о динамике ионосферных неоднородностей [7–9]. Точность и эффективность современных моделей (эмпирические [10, 11], физические [12–14] и нейросетевые [3, 15, 16]) во многом зависят от наличия качественных геофизических данных (используются индексы магнитной и солнечной активности, спектры солнечного ультрафиолетового излучения, температура и плотность нейтрального состава атмосферы), определяющих состояние околоземного космического пространства и используемых в моделировании. Поэтому наибольшие погрешности современных моделей наблюдаются в области высоких широт и в районах с редкой сетью наблюдений данных [12–15, 17]. Также достоверность этих методов существенно снижается в возмущенные периоды [1, 3, 12–15, 17].

В статье представлены результаты, продолжающие исследование в рамках направления работ [6-9, 18]. В данной работе описана модифицированная многокомпонентная модель временного ряда параметров ионосферы (ММКМ). Предлагаемая модель включает регулярные разномасштабные компоненты, описывающие как длительные вариации параметров ионосферы, так и короткопериодные колебательные процессы. Возмущённые компоненты модели описывают внезапные аномальные изменения разномасштабной структуры, характеризующие возникновение ионосферных неоднородностей. Идентификация модели основана на комплексном подходе, объединяющем разные схемы вейвлет-преобразования и авторегрессионные модели. Ввиду наличия численно устойчивых быстрых алгоритмов преобразования данных и большого разнообразия базисных функций с компактными носителями вейвлет-преобразование позволяет выполнять детальный анализ сложных структур данных [19-21], в том числе в области геофизики [22-26]. На основе модели разработан алгоритм анализа ионосферных параметров, позволяющий в оперативном режиме выделять интенсивные ионосферные аномалии, характеризующие возникновение сильных ионосферных бурь. С использованием алгоритма выполнен анализ часовых и 15-минутных данных критической частоты ионосферы foF2. Анализировались периоды магнитных бурь за 2015-2017 гг., использовались данные foF 2 станций регистрации «Паратунка», «Москва», «Норфолк» (Австралия) и «Вакканай» (Япония). В анализируемые периоды выделены длительные интенсивные аномальные изменения во временном ходе foF2, что подтверждает эффективность предлагаемого алгоритма.

Описание алгоритма

В работах [8, 18] показано, что временной ряд параметров ионосферы f ( t ) может быть представлен в виде модифицированной многокомпонентной модели (ММКМ):

f ( t ) = A РЕГ ( t ) + £И озм ( t ) + e ( t ) = n

(                          )              (1)

= 2 а^ц ( t ) +1 2 р П р^ ( t ) + £ р м.м ( t ) I + e ( t ),

Ц= 1 Д V n>n 1             П^П 1           )

где

A РЕГ ( t ) = 2 а^ц ( t )

H= 1 T

( ц = 1, T - номер компоненты) - составляющая, описывающая регулярные вариации параметров ионосферы, включает компоненты а^ц ( t ), определяемые солнечной активностью и локальными факторами;

Е ₽ Позм ( t ) Е в ср- ( t ) + ^ р м. ( t ) - n              П>П 1              П^П 1

возмущённая составляющая, описывающая внезапные короткопериодные аномальные изменения (идентификация данной составляющей подробно представлена в работах [7, 8]), где компонента

£ Р П р.м ( t )

n>n 1

описывает умеренные локальные аномалии, а компонента

2 pm. ( t )

n^m описывает локальные аномалии малой интенсивности (предполагается, что компоненты

E P S- ( t ) и £ э м.м ( t )

П>П 1                П^П 1

аддитивны); e ( t ) - случайная составляющая, включающая помехи искусственного происхождения (запуски ракет, промышленные взрывы и др.), а также аппаратные сбои.

Используя алгоритм выделения регулярных компонент а^ц ( t ), основанный на быстрых вейвлет-разло-жениях (КМА) и представленный в работах [7, 9], регулярная составляющая А ^РЕГ( t ) (см. (1)) может быть представлена в виде [7, 8]:

A ^РЕГ ( t ) = f - m рт ( t ) + Е g jp„ ( t ),                        (2)

jрег где f- mpt (t) = E

k

c - m ^рег , k ^Ф - m ^рег , k

⁽ t ) ^-

сглаженная компонента, описывающая длительные изменения временного ряда масштаба mрег (определяет компоненту a1 (t )), c-mрег,k   \J , ф-mрег,k коэффициенты разложения,

Ф-m рег, k (t) = 2-m рег/2 Ф(2-m рег t - k ) - скейлинг-функция, gjрег(t) = Е djрег, k ^ k jрег, k

⁽ t ) ^-

детализирующая компонента масштаба jрег = -1, -mрег описывает короткопериодные колебательные изменения (определяет компоненту ац(t), где ц = 2, T ), djрег, k = ( f, ^ jрег, k) - коэффициенты разложения характеризуют амплитуду колебания (величину отклонения от тренда (характерного уровня)) в момент времени t = k,

Yjp,r,k(t) = 2jP'r/2^(2jP'rt-k) - вейвлет.

Используя методы авторегрессии проинтегрированного скользящего среднего (АРПСС) [27, 28], регулярная составляющая А ^РЕГ( t ) (см. соотн. (2)) может быть представлена в параметрическом виде [6-9]:

A ^РЕГ ( t ) = 2 Е   ^ Ц Рег , k b Ц Р егЛ ( t ),

Ц= 1, T k = 1, N ^ц

’ j ре ^г

где p ц                          h ц jрег                                     jрег хи = YV"  „ц _уАц „ц sjрег,k    У Y jрег,lШjрег,k-1    У Jрег,najрег,k-n l=1                            n=1

оценочное значение регулярной ц -й компоненты, p ¹¹рег , у " _рег l - порядок и параметры авторегрессии ц -й компоненты, h ^ц рег , 9 " _рег n - порядок и параметры скользящего среднего ц -й компоненты, «^ц _рег k = V^v ' S ' j _рег k , v " - порядок разности ц -й компоненты, 5 - m рег k = c - _mрег , _k ,

5"рег k = djре,,k , ц = 2, T , T - количество моделируемых компонент, а"рег k - остаточные ошибки модели ц-й компоненты, Njрег - длина ц-й компоненты, b1 mрег,k =Ф—mр'г,k - масштабирующая функция, bцрег , = Т ,рег k, ц = 2, T - вейвлет-базис ц-й компонен-, k            j , ты.

Сильные ионосферные аномалии приводят к существенным изменениям временного хода данных ионосферы (напр. [1, 17]). Поэтому естественно предположить, что в периоды возникновения сильных ионосферных возмущений произойдёт изменение регулярного хода ионосферных данных и возрастут остаточные ошибки регулярной составляющей А ^РЕГ( t ) (см. соотн. (3)). Тогда операция их выделения может быть основана на проверке условия:

г/ jрег

Q ц

УI а тт- / ¹ j ^рег , k + q q = i

¹ >  H ц , j рег ,

где п"       _ „ц,факт _ ц,модель > г ajрег,k + q    sjрег,k + q   sjрег,k+q , q - 1

шаг упреждения данных, ц,модель sjрег, k

p j рег                                   h j рег

У 7црег , l to"рег , k + q -1 - У 9црег , na"рег , k + q _ n , Q ц l = 1                                n=1

длина упреждения данных на основе модели ц -й компоненты, H ^ j рег - пороговое значение ц -й компоненты, определяющее наличие аномальных изменений в ц -й компоненте.

Следуя результатам работы [27], пороговое значение H _ц j рег (см. соотн. (4)) может быть определено на основе оценки дисперсии ошибок модели:

[     Й .-1            ²

^Гj ( Q " ) =^ + У^ рег , q )

1/2

'    О а "   , jрег

где у"   - весовые коэффициенты модели ц-й ком- р~ , q поненты, о2 - дисперсия остаточных ошибок мо-ajрег дели ц-й компоненты.

Либо с учётом вероятностных пределов:

[ Д-1            ² '

'j ( Q ^ ) = U ^ /2 1 + £ ( ^ рег , q )

1/2

о а "  , _j рег

где и ^ /2 - квантиль уровня (1 - ^ /2) стандартного нормального распределения.

Поскольку амплитуда ошибки a "„_{г k + q} характеризует на масштабе j ^рег величину отклонения фактического значения функции от её характерного значения (см. соотн. (4)), интенсивн ость аномалии на масштабе j ^рег в период t = k + 1, k + L " может быть оценена как

У" _____ j рег, k+1, k+Lц

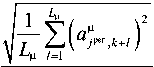
^H ц , у -^р "г

где L ц - длина скользящего временного окна.

Таким образом, процедура выделения интенсивных аномальных изменений во временном ряде параметров ионосферы может быть основана на применении алгоритма:

• 1.    Загружаем в память данные, на основе КМА выполняем разложение до уровня m = m ^рег и получаем их представление в виде:

• 2.    На основе предварительно оцененных моделей компонент

• 3.    Вычисляем остаточные ошибки моделей:

• 4.    Периоды времени t = k +1,

  ., k + Q ц , для которых

  
  

  ^ц

  j рег

  
  

• 5.    Оцениваем интенсивность выделенных аномалий

  Y ^ц _____

  j ^рег , k + 1, k + L ц

  
  
  

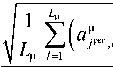
  H ц , j рег

  
  

f(t) = f-mрег(t) + У gjрег(t)• jрег

f „рег ( t ) = У S ¹ _г , Ь ¹ , ( t ) и

J - mр \                     - mрег, k - mрег, k k=1, N ц ’ - mрег

T

У g j Pег ⁽ t ) = У У s ц рег J b " рег k ⁽ t )

jрег                ц = 2 k=1, Nj"рег выполняем моделирование.

пц       _ ?ц,факт _ ц,модель ajрег, k + q sjрег, k + q sjрег, k+q .

Q ц ^ц

^{У 1} a j ^рег , k + q q = 1

ц , j ^рег ,

принимаем за аномальные.

Результаты экспериментов

Результаты обработки ионосферных данных представлены в табл. 1 (использовались часовые данные foF 2 станций «Паратунка» (53,0 ° СШ и 158,7 ° ВД), «Вакканай» (Япония, 45,16 ° СШ и 141,75 ° ВД) и Норфолк (Австралия, -35,6 ° СШ и 160 ° ВД)), которые показывают эффективность предлагаемого алгоритма. В периоды умеренных и сильных магнитных бурь на всех анализируемых станциях наблюдались длительные интенсивные ионосферные аномалии, о чём свидетельствует возрастание остаточных ошибок ММКМ (см. соотн. (4)): превышение составляло от 1,8 СКО до 5,6 СКО. Длительность выделенных аномалий зависела от силы бури и составляла: для умеренных магнитных бурь (Kp: 3-5) - от 27 до 39 ч, для сильных магнитных бурь (Kp: 6-8) - от 36 до 68 ч.

Табл. 1. Результаты обработки ионосферных данных (foF2) в периоды магнитных бурь 2015–2017 гг.

Дата события / время начала (UT) / характер события: ПН – постепенное начало, РН – резкое начало / сила бури	Станция	Наличие (отсутствие): превышение СКО (70% доверительный интервал) / длительность
21.01.15/ 14:10/ ПН/Kp 4	Паратунка	2,1 СКО / 27 ч
17.02.15/ 4:45/ ПН/ Kp 4	Паратунка	5,6 СКО / 29 ч
	Вакканай	3,3 СКО / 34 ч
21.06.15/ 16:55/ РН/ Kp 4	Паратунка	3,8 СКО / 27 ч
09.02.16/ 9:00/ РН/ Kp3	Паратунка	1,8 СКО / 39 ч
19.12.15/ 16:18/ РН/ Kp 6	Паратунка	5,6 СКО / 42 ч
	Норфолк	2,6 СКО / 36 ч
24.11.16/ 00:00/ РН/ Kp5	Паратунка	3,9 СКО / 33 ч
17.03.15/ 4:45/ РН/ Kp 8	Паратунка	5,6 СКО / 65 ч
	Вакканай	3 СКО / 37 ч
20.09.15/ 06:05/ РН/ Kp 7	Паратунка	3,5 СКО / 68 ч
07.09.17/ 23:00/ РН/ Kp 8	Паратунка	3,2 СКО / 66 ч

На рис. 1 и 2 в качестве примера представлены результаты апробации предложенного алгоритма, полученные для 15-минутных данных критической частоты ионосферы ( foF 2) станций «Паратунка» (53,0 ° СШ и 158,7 ° ВД) и «Москва» (55,5 ° СШ и 37,3 ° ВД).

В первый анализируемый период (06.09– 12.09.2017 г., рис. 1) вследствие прихода ускоренного

а) 06.09 07.09 08.09 09.09 10.09 11.09 12.09

в) 06.09 07.09 08.09 09.09 10.09 11.09 12.09

д)   06.09 07.09 08.09 09.09 10.09 11.09 12.09

ж) 06.09 07.09 08.09 09.09 10.09 11.09 12.09

Рис. 1. Результаты моделирования ионосферных данных foF2 ст. «Паратунка» (а-в) и ст. «Москва» (г-е): а), г) foF2 (черным), медианные значения (серым); б), д) ошибки моделей компонент – f –5 ( t ) (черным), g –5 ( t ) (серым) и их СКО; в), е) интенсивность выделенных аномалий – f –5 ( t ) (черным), g –5 ( t ) (серым); ж) K-индекс геомагнитной активности ст. «Паратунка»; з) Dst-индекс

На рис. 2 представлены результаты моделирования временного ряда foF2 за период 06.11 – 11.11.2017 г. В анализируемый период из-за прихода в начале суток 7 ноября неоднородного ускоренного потока (CIR) от обширной корональной дыры (по данным наблюдается повышение геомагнитной активности (K-индекс >3). Оценка остаточных ошибок модели (см. соотн. (4)) показывает наличие длительных (46 часов (Москва) и более 3 суток (Паратунка)) и интенсивных (рис. 2 в, е) аномальных изменений во временном ходе foF2 для анализируемых станций: для компоненты f–5 (t ) – 3,8 СКО (Па- потока от корональной дыры и выброса корональной массы (CME) произошла магнитная буря 07.09– 08.09.2017 г (K-индекс >3) (по данным .

Результаты обработки данных (см. рис. 1) показывают схожий характер поведения ионосферы на анализируемых станциях в период события. Наблюдается существенное возрастание остаточных ошибок модели (рис. 1 б , д ), что говорит о наличии длительных (более 4 суток) и интенсивных (превышение от 2 СКО до 7,5 СКО) аномальных изменений во временном ходе параметров ионосферы (рис. 1 в , е ). Наиболее существенное возрастание ошибок наблюдалось в восстановительную фазу магнитной бури 08.09.2017 и составило: для компоненты f –5 ( t ) – 5,4 СКО (Паратунка) и 7,5 СКО (Москва), для компоненты g –5 ( t ) – 3,5 СКО (Паратунка) и 2,8 СКО (Москва). Полученные результаты согласуются с традиционным медианным методом – наблюдаются существенные отклонения значений foF 2 от 27-дневной медианы. Но, в отличие от медианного метода, предлагаемая модель позволяет чётко выделить аномальный период в ионосфере и оценить его параметры (временную длительность и интенсивность).

6 0

• б)    06.09 07.09 08.09 09.09 10.09 11.09 12.09 МГц 8 4 0

  

  г) 06.09 07.09 08.09 09.09 10.09 11.09 12.09

  Y^.k 6 3 0

  
  

е) 06.09 07.09 08.09 09.09 10.09 11.09 12.09 нТл 0 -100 -200

з)    06.09 07.09 08.09 09.09 10.09 11.09 12.09

ратунка) и 5 СКО (Москва), для компоненты g –5 ( t ) – 2 СКО (Паратунка) и 3,5 СКО (Москва). Сопоставление с медианным методом (см. рис. 2 а, г ), аналогично рассмотренному выше событию, подтверждает эффективность разработанной модели.

Заключение

Разработанная модель и построенный на ее основе вычислительный алгоритм позволили выполнить анализ временного хода параметров ионосферы (foF2) в периоды повышенной геомагнитной активности. Анализ результатов показал, что в периоды магнит- бурь, произошедших в 2015–2017 гг.) подтвердили эффективность предлагаемого в работе алгоритма для задач анализа ионосферных данных и выделения ионосферных возмущений.

ных бурь регулярный ход foF2 существенно меняется, что приводит к возникновению длительных аномалий во временном ряде foF2 . Выполненные статистические оценки (выполнен анализ 10 магнитных

МП,

а) 06.11    07.11     08.11     09.11     10.11     11.11

б)   06.11    07.11     08.11      09.11      10.11      11.11

в)

3 -

2 "

06.11    07.11     08.11     09.11     10.11     11.11

МП; 10

06.11    07.11     08.11     09.11     10.11     11.11

г)

Рис. 2. Результаты моделирования ионосферных данных foF2 ст. «Паратунка» (а-в) и ст. «Москва» (г-е): а), г) foF2 (черным), медианные значения (серым); б), д) ошибки моделей компонент – f –5 ( t ) (черным), g –5 ( t ) (серым) и их СКО; в), е) интенсивность выделенных аномалий – f –5 ( t ) (черным), g –5 ( t ) (серым); ж) K-индекс геомагнитной активности ст. «Паратунка»; з) Dst-индекс

Автор выражает благодарность институтам, выполняющим регистрацию ионосферных и геомагнитных данных, которые использовались в работе, а также центру коллективного пользования «Северовосточный гелиогеофизический центр».