Алгоритм высокоточного сопровождения вторичных источников оптического излучения и его эффективность

Задача автоматического сопровождения движущихся объектов предусматривает наличие в контуре управления измерителя, предназначенного для оптимальной (квазиоптимальной) оценки текущих координат объекта по информации, заключенной в сигналах различной физической природы. В качестве источника такой информации может использоваться изображение факела двигателя управляемого боеприпаса. В этом случае управление системой сопровождения возможно с помощью матричного датчика, формирующего изображение факела двигателя как вторичного источника оптического излучения. Поскольку координаты энергетического центра изображения факела двигателя управляемого боеприпаса с достаточной точностью определяют его текущее местоположение, возникает задача разработки алгоритма определения координат движущегося объекта по изображению визируемой сцены и вторичного источника оптического излучения (факела двигателя).

Постановка задачи

Задачу синтеза алгоритма определения координат будем решать на основе использования аппарата нелинейной пространственно-временной фильтрации [1-3]. Аппроксимируем движение объекта в плоскости, перпендикулярной линии визирования матричного датчика, системой стохастических дифференциальных уравнений:

д X ( t )     X ( t )            д Y ( t )      Y ( t )

—5— = —г + nx (t);    r,       r +ny(t)’ д t T              д t       T xy где X(t), Y(t) - текущие координаты объекта по горизонтальной и вертикальной осям в картинной плоскости, рассчитываемые относительно центра изображения, определяемого по-– 1145 – ложением линии визирования цели; Tx, Ty - эквивалентные постоянные времени; nx, ny - нормальные белые шумы с нулевым математическим ожиданием и спектральными плотностями Nx, Ny.

Полезный сигнал (изображение факела двигателя), наблюдаемый на текущем изображении визируемой сцены и являющийся функцией интересующих нас параметров, формально представим двумерным экспоненциальным законом вида

( X ( t ))² ( Y ( t ))²

5(x yt) = Ae" 2R. (t)2 e" 2Ru (t)2 (2) .У. , где A - амплитуда наблюдаемого полезного сигнала; Ru (t) = Ruq + ARu (t) - эквивалентный радиус изображения факела двигателя; ARu (t) - приращение эквивалентного радиуса к априорному значению Ru0 .

Дополним систему уравнений (1) дифференциальным уравнением для значений приращения эквивалентного радиуса изображения факела двигателя

SA R uX t ) ^A R uy) + n R _{( t} ),                                         (3)

R где TR - эквивалентная постоянная времени; nR - нормальный белый шум с нулевым математическим ожиданием и спектральной плотностью NR.

Представим пространственно-яркостную структуру наблюдаемого текущего изображения следующим выражением:

и ( x , у , t ) = f ( x , у ) + s ( x , у , t ) + n ( x , у , t ),                                            (4)

где f ( x , y) - исходное изображение сцены в отсутствие движущегося объекта; n ( x , y , t ) - гауссовский однородный пространственно-временной шум наблюдения со спектральной плотностью N и корреляционной функцией вида

r (A x , A y , A t ) = N 5(A x , A y )5(A t ),                                                (5)

где δ(Δ x , Δ y ), δ(Δ t ) – δ–функции от приращений пространственных и временной переменных соответственно.

Теперь задача синтеза алгоритма определения координат движущегося объекта может быть сформулирована как задача совместной оценки по наблюдаемому изображению (4) переменных X , Y, ЛR u , изменение которых во времени определяется уравнениями (1) и (3).

Синтез алгоритма высокоточного сопровождения

Введем единообразную систему обозначений оценок переменных Xi, Y , K R< u , подлежащих определ нию

А       А А А .        А А      А

X = ( Х 1 , ^ 2 , 2 ₃ ) = ( X , Y , A R u ).

Тогда в соответствии с [2] в гауссовском приближении квазиоптимальные оценки пере-„    „    „

М^{енных (} Л , ^ 2 , Л , ) ^по наблюдаемому изображению и ^{( x} , у , t ) представляются следующими ^выражениями в векторно-матричной форме:

dX! dt = a( t, X) + R(t)F1( t, X),(7)

dR , d = N + a,( ,.w + R№aT(,, X) + R№(., X)R(.),, где a(t, X) = (-X1 / Tx, - X2 / Ty, -X3 / TR)T ; a1(t, X) - матрица размерности 3x3 с элементами А      А            А              А      А              А      АА ay =дai(t,ЬУд^; F1(t,^) =(dF(t,^Уд%-,дF(t,^Уд^зУ F2(t,^) - матрица размерности 3x3 с элементами Fij = d2F2(t,X)/ dijdij; N - диагональная матрица размерности 3x3 с элементами Nn = Nx, N22 = Ny, N33 = NR ;

F ⁽ t , ^{x )} =^-^7 Я [ u ^{( x} , y , t ) ^{- (} f ^{( x} , y ) ^{+ 5 ( x} , y , t ^{))] 2} dxdy

² N M

– функционал правдоподобия [3]; M – область определения изображения.

Определение дискриминационных характеристик алгоритма

Рассмотрим более подробно элементы д F ( t , X )/ d^ i вектора F ^ ( t , X ), математические ожидания которых можно интерпретировать как дискриминационные характеристики многосвязной следящей системы, устанавливающие связь между наблюдаемым текущим изображением сцены и регулирующим воздействием по соответствующей координате. По аналогии с [4-7] упростим выражение (9) для функционала правдоподобия F ( t , X ). После возведения в квадрат подинтегрального выражения, перегруппировки слагаемых и исключения из дальнейшего рассмотрения слагаемых, не зависящих от оцениваемых переменных, выражение для функционала правдоподобия может быть представлено в упрощенном виде:

2           2

2+(v

F ( t, X ) = A JJ u ( x , y, t ) exp( - l x- ^ 12 ⁽ y ^ ²⁾ ) dxdy .                   (io)

N^{M              2(} R u ^{0 +}

^{Теперь после дифференцирования} выражения ^{(10) по} Л 1 , Л ₂, Л з элементы ^{вектора} F 1 ⁽ t , X ) принимают следующий вид:

„       - ( X - i ^)2 + ( ,-^ 2 ?

дF(,,^ SA, = -flu(X.y,,)(RUo0 + ^J^)2 e   2^.*У   dxdy,

.      - ( x - 2 1 ) 2 + ( y - ^ 2 ) 2

dF(t,i)Zd.i2 = A JJu(x,y,t) y-Л? 2 e   2(Ru•+V'  dxdy,(12)

N^{M       (} R u ^{0 +} Я , )

A«< x -   +(.- d( t,)d A3 = ^Jf u (x. y,t)     ([iu 0 + ;.3)3     e                  dxdy-. (3)

На рис. 1 представлена дискриминационная характеристика сист е мы слежения за координатами центра изображения факела двигателя в горизонтальной плоскости, рассчитанная с помощью вырэжения (11) и определяющая зависимость сигнала управления на выходе дискриминатора от ошибки оценивания координат X i - X i (Х₁ - истинное значение координаты объекта в горизонтальной плоскости, измеряемое в элементах разрешения (э. р.) изображения). Дискриминационная характеристика рассчитана для следующей совокупности исходных данных:

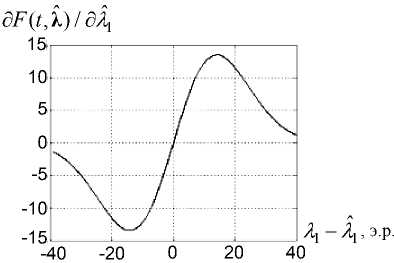
Рис. 1. Дискриминационная характеристика системы слежения за координатами

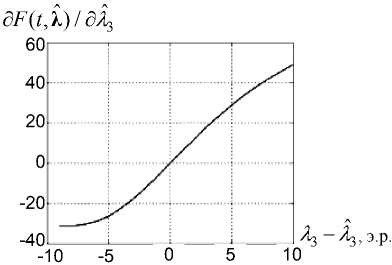
Рис. 2. Дискриминационная характеристика системы слежения за приращением радиуса

А

A =1; Л 2 - Х 2 =0 э. р.; R u о =10 э. р.; Л 3 =0 э. р. В качестве изображения фона f ( x , у ) использовалось си тезированное ме дами комп ю ерной графи и гауссовское случайное поле с заданными параметрами закона распределения яркостей элементов изображения ( т ф = 0, о ф = 0,1 - ма^{тематичес}кое ожидание и СКО яркости элементов изображения фона) и изотропными корреляционными войствам .

Из рис. 2 представлена дискриминационная характеристика системы слежения за при-раще ием экви а е тного а и са из р жения факела двигателя, рассчитанная с помощью вы ения (1 ) (λ₃ – и тинное значение приращения эквивалентного радиуса), при условии, что A =1; 5 1 - 5 1 =0 э. р.; 5 2 - 5 2 =0 э.р.; R u о =10 э. р. Из рис. 1 и 2 видно, что дискриминационные характеристики в окрестности истинных значений параметров линейны.

Уточнение дифференциальных уравнений квазиоптимальной фильтрации

Си Стема диф ^ференцИ^альных уравнений ^{квазиоптимально}й фильтрации, полученная ^{с по}мощью (7), (11) - (13) в предположении о некоррелированности ошибок оценки рассматриваемых параметров ( R y = 0, при i ^ j ) и соответствующая выражениям (1) - (4), имеет вид

_{ˆˆ                         ˆ     -} ( x - λ ^ˆ 1 )² + ( y - λ ^ˆ 2 )²

^{∂ λ 1} =- ^{λ 1} + ^{AR 11} u ( x , y , t )    ^{x - λ 1}    e    ^{2( R u 0 + λ ˆ3)2} dxdy ,

∂ tT x    N M ^∫∫       ( R u 0 + λ ^ˆ 3 ) ²

А А         А А

_- ( x - λ 1 )² + ( y - λ 2 )^{2 ∂ λ 2} =- ^{λ 2} + ^{AR 22} u ( x , y , t )    y ^{- λ 2}    e    ^{2( R u 0 + λ ^ ˆ3)2} dxdy ,

∂ tT y    N M ^∫∫       ( R u 0 + λ ˆ 3 ) ²

А         А

∂ λ _{3 =-} λ ₃ ∂ t ^=- T R ⁺

AR

³³ ∫∫ u ( x , y , t ) N_M

А П          А п

( x - λ ^ˆ ₁ ) + ( y - λ ^ˆ ₂ )

( R u 0 + λ ^ˆ 3 ) ³

( x - λ ₁)² + ( y - λ ₂)²

_e     2( R u 0 + λ 3 )    _{dxdy .}

Общая структура синтезированного алгоритма пределения коорди ат движ г ся объекта, соответствующая (14), приведена на рис. 3. Она представляет собой схем у многоканальной следящей системы, осуществляющей слежение за центром и обра ения ф к ла двигател я. П ^ри этом замыкание петель обратной связи производится по переменным Л 1 и Л 2

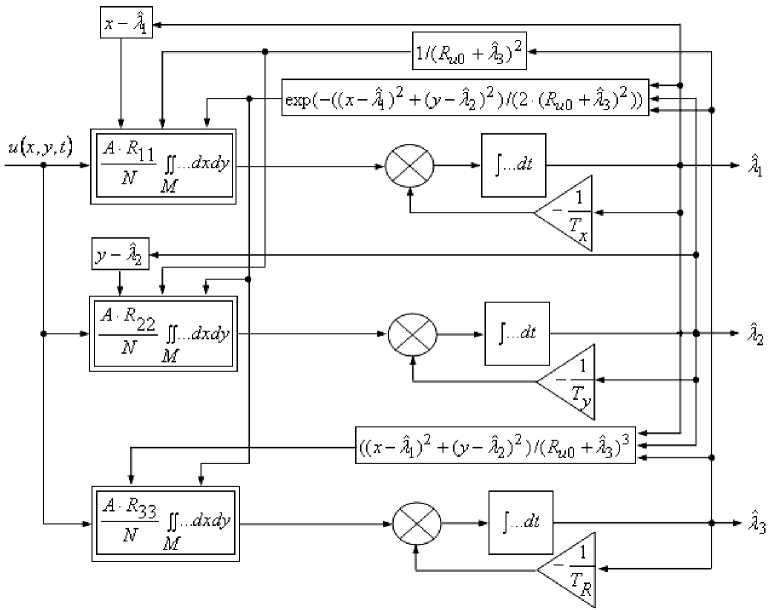
Рис. 3. Структура синтезированного алгоритма

, являющимея оценка ми координат движущегося объекта. О с обенность данной системы заключается в возмо ности слеж н я за риращением эквивалентного радиуса изображения факела двигателя Я 3 и последующего использования для обработки не только всего наблюдаемого изображения, ограниченного областью M , но и части наблюдаемого изображения, ограниченного пространственным стробом с размерами сторон, пропорциональными значению текущего радиуса.

При этом наличие пространственного строба, в пределах которого выполняется обработка, является существенным фактором, определяющим высокую помехозащищенность синтезированного алгоритма от преднамеренных помех.

Исследование эффективности синтезированного алгоритма

С использованием выражений (14) разработана имитационная модель системы слежения, которая позволила провести оценку точности определения текущих координат движущегося объекта. В качестве показателя эффективности использовалось СКО ошибок измерения оцениваемых текущих параметров полезного сигнала относительно заданных при моделировании.

В качестве изображений фона в разработанной модели применены синтезированные методами компьютерной графики гауссовские случайные поля с заданными параметрами закона распределения яркостей элементов изображения ( т ф = 0,5, о ф = 0,1) и изотропными корреляционными свойствами.

В цепи отрабо тки ошибок слежения в модели использовались динамические 3 венья с пере - ат ной нкци й разомкнутой петли отработки этих ошибок вида

K p (Tp +1)

На вход этой

передаточной функции с параметрами K = 15 V, T = 0,03 c подавались сигналы управления ^с

, дF (t , X ) д F (t , X )

с диск^рими„аторо. ( . ..    -^

дF (t, X) — / дХз

А    А     А

), а с выхода снимались сигналы Я ^ , Я 2 , Я 3 .

Коэффициенты R _{1 1}, R ₂₂, R _{^ 33} определялись заблаговременно решением стационарной системы обыкновенных дифференциальных уравнений (8). Значение эквивалентного радиуса изображения факела двигателя R и 0 составляло 10 элементов разрешения.

В результате имитационного моделирования процесса слежения за координатами объекта, движение которого представлялось как случайный процесс с нулевым математическим ожиданием,среднеквадратическим отклонением порядка 15 элементов разрешения и интерва-2

…3 с, установлено, что синтезированный алгоритм обеспечивает устойчивое слежение за координатами движущегося объекта с ошибкой не более двух элементов разрешения (а0 = 2), что позволяет сделать вывод о его достаточно высокой эффективности.

Кроме того, получены результаты, давшие возможность оценить эффективность функционирования синтезированного алгоритма. На рис. 4 сплошной линией представлен нормированный к о₀ график зависимости изменения СКО ошибок измерения координат движущегося объекта от отношения реального значения эквивалентного радиуса изображения факела двигателя к априорно заданному ( R_и / R_{и 0}) при отсутствии канала слежения за эквивалентным радиусом изображения факела двигателя.

Видно, что алгоритм обеспечивает устойчивое слежение за координатами движущегося объекта с ошибкой не более трех элементов разрешения при условии, что значение реального эквивалентного радиуса отличается от априорно заданного не более чем в 2 раза. В противном случае ошибки слежения значительно возрастают (в 2 раза и более).

Пунктирной линией на рис. 4 представлен нормированный график зависимости изменения СКО ошибок измерения координат объекта от отношения реальной интенсивности изо-

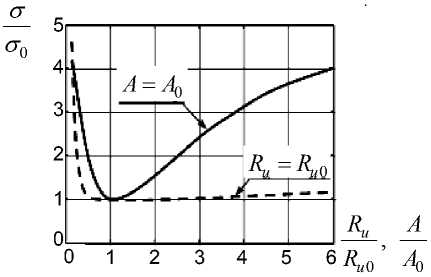
Рис. 4. Нормированные графики зависимости о / ао от Ru / Ru 0 ( —) и А / А о (—)

бражения факела двигателя к заданной априори ( А /А ₀) (при наличии канала слежения за эквивалентным радиусом изображения факела двигателя). Полученные результаты позволяют сделать вывод о том, что несоответствие значений реальной амплитуды полезного сигнала и априорно заданной практически не влияет на качество слежения за текущими координатами движущегося объекта с помощью разработанного алгоритма. Это объясняется тем, что изменения значений реальной амплитуды полезного сигнала приводят к изменению значений оцениваемого эквивалентного радиуса изображения факела двигателя и также косвенно учтены в структуре синтезированного алгоритма.

Заключение

С использованием аппарата нелинейной пространственно-временной фильтрации синтезирован алгоритм определения координат движущегося объекта по изображению визируемой сцены и факела двигателя управляемого боеприпаса как вторичного источника оптического излучения. Результаты синтеза положены в основу имитационной модели системы слежения, воспроизводящей процесс работы алгоритма и выработки команд в контур высокоточного сопровождения объекта.

Проведена оценка точности слежения за текущими координатами движущегося объекта в условиях отсутствия достоверной информации о параметрах изображения факела двигателя. Полученные результаты говорят об эффективности синтезированного алгоритма и возможности его использования для высокоточного сопровождения объектов с вторичными источниками оптического излучения.