Алгоритмические методы обеспечения электромеханической совместимости асинхронных электроприводов при питании от преобразователей частоты

Под электромеханической совместимостью в электроприводах понимают способность электропривода нормально функционировать при питании от источника, не обеспечивающего нормированное качество электроэнергии, и не оказывать недопустимого влияния на работу исполнительного механизма электропривода [1, 2].

В современных частотно-регулируемых электроприводах переменного тока на основе асинхронных электродвигателей (АД) с короткозамкнутым ротором, выходное напряжение автономного инвертора представляет собой высокочастотную последовательность прямоугольных импульсов, длительность которых изменяется по синусоидальному закону, поэтому выходное фазное напряжение может быть представлено рядом Фурье [3, 4]:

µU

UфA =   DC sin(Ωt) + ∑ UmM sin(mωнt) + m=∞ n=∞

+ ∑ ∑ UnM sin(mωн ±nΩ)t,(1)

m = 1 n = 1

где µ – коэффициент модуляции, его величина задается системой управления и может регулироваться в диапазоне от 0 до 1; U_DC – постоянное напряжение на входе инвертора; Ω – частота основной гармоники на выходе инвертора; ω _н = 2 π f_ШИМ – несущая частота или частота широтно-импульсной модуляции напряжения инвертора.

То есть выходное фазное напряжение статического преобразователя содержит: основную гармонику напряжения, частота которой равняется Ω , а амплитуда равна µUDC /2 (частота и амплитуда напряжения могут плавно регулироваться системой управления электропривода); гармоники напряжения, частоты которых кратны несущей частоте ωн , амплитуды которых равны UmM ; комбинационные гармоники, частоты которых равны сумме и разности несущей и основной гармоник mωн ± nΩ с амплитудами UnM .

Гармонические составляющие напряжения статора вызывают появление соответствующих гармоник тока и магнитного потока, которые можно разложить в гармонический ряд следующим образом [4]:

Icт = Im sin(Ωt+ ϕ) +m∑=∞ImM sin(mωнt) + m=1

m =∞ n =∞

+ ∑ ∑ I_nMsin(m ω _н ± n Ω )t;             (2)

m = 1 n = 1

Ψ _рот = Ψ _msin( Ω t + ϕ ₂) + ^m ∑^=∞ Ψ _mM sin(m ω _нt) + m = 1

m =∞ n =∞

+ ∑ ∑ Ψ _nMsin(m ω _н ± n Ω )t,           (3)

m = 1 n = 1

где I_m , Ψ _m – амплитудные значения тока статора и потокосцепления ротора.

Взаимодействие гармоник тока статора и потокосцепления ротора одного порядка создают постоянные электромагнитные моменты. Уравнение такого момента можно записать в следующем виде:

M (n) = I ст(n) Ψ рот(n) sin( θ (n) ) .                  (4)

При взаимодействии гармонических составляющих тока статора и потокосцепления ротора разного порядка, частота вращения и угол между которыми разные по величине и изменяются во

Электромеханические системы времени, создаются пульсирующие электромагнитные моменты, которые можно описать следующим уравнением:

M (ip) = I ст(i) Ψ рот(p) sin( θ (ip) ), (5) где M_(ip) – высокочастотная гармоника электромагнитного момента, которая создается в результате взаимодействия i -й гармоники тока статора и p -й гармоники потокосцепления ротора, между которыми образуется ip -й угол; I_ст(i) – высокочастотная гармоника тока статора; Ψ _рот(p) – высокочастотная гармоника потокосцепления ротора; θ _(ip) – угол между i -й гармоники тока статора и p -й гармоники потокосцепления ротора.

Анализ выражений (1)–(5) показывает, что при увеличении частоты ШИМ возрастают как частоты гармоник напряжения, кратные несущей частоте ω _н , так и частоты комбинационных гармоник m ω _н ± n Ω . Отсюда можно сделать вывод, что для обеспечения электромеханической совместимости приводного двигателя с преобразователем целесообразно частоту широтно-импульсной модуляции устанавливать по возможности наиболее высокой. В этом случае токи обмотки статора, обусловленные высшими гармониками напряжения, будут малы, что объясняется большим индуктивным сопротивлением на повышенных частотах. Отсюда следует, что колебания электромагнитного момента не будут существенно ухудшать вибро-акустические показатели двигателя.

В данной публикации рассмотрено влияние несинусоидального выходного напряжения стати- ческого преобразователя на АДи, сформированы рекомендации по обеспечению электромеханической совместимости преобразователя с двигателем.

Схема, модель и параметры асинхронного электропривода

Функциональная схема системы векторного регулирования скорости представлена на рис. 1. Система регулирования построена в системе координат dq, вращающейся вместе с управляемым вектором потока ротора, для чего выполнены соответствующие координатные преобразования. В такой системе дифференциальные уравнения, описывающие двигатель, принимают простейший вид, а управление вектором сводится к управлению величиной и знаком его проекций на соответствующие оси. Система содержит регулятор скорости (ПИ-РС), задающий необходимый электромагнитный момент двигателя (M^*), изменение которого осуществляется векторным регулятором статорного тока, состоящего из двух скалярных регуляторов d и q (ПИ-РТ d и ПИ-РТ q ) и использующего в качестве обратной связи измеренный и преобразованный в систему dq реальный вектор статорного тока. Регулятор тока формирует в системе dq вектор напряжения статора, характеризующийся двумя составляющими: u sd и u sq , которые переводятся в неподвижную систему координат αβ, связанную со статором, затем преобразуются векторным модулятором в сигналы управления драйверами транзисторных модулей АИН, а он, в свою очередь, формирует питающее двигатель напряжение [5, 6].

Для рассматриваемой функциональной схемы векторного регулирования скорости АД разрабо-

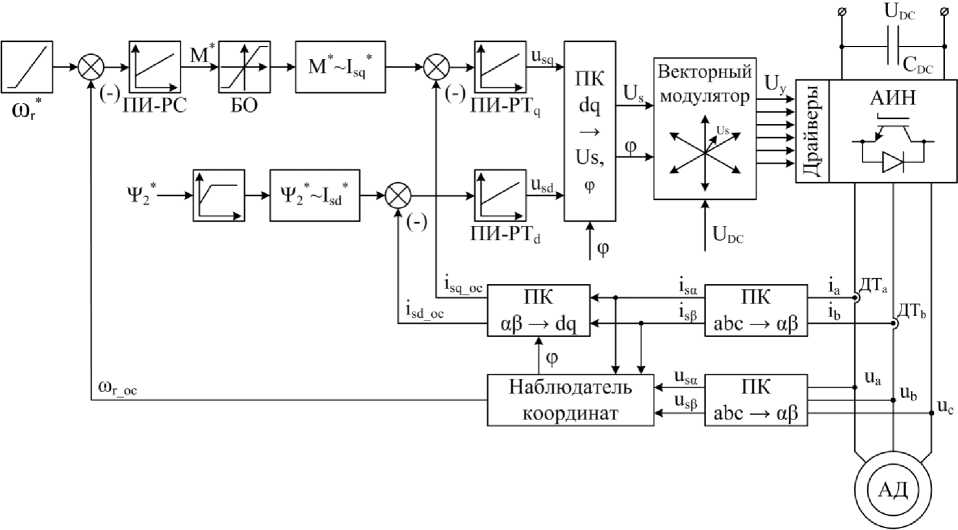
Рис. 1. Функциональная схема системы векторного регулирования скорости АД в осях dq

Татаринов Д.Е., Козярук А.Е.

тана компьютерная модель электропривода в MATLAB-Simulink, представленная на рис. 2 и 3. Изменение параметров Т-образной схемы замещения в компьютерной модели АД не учитывается в связи с отсутствием необходимости точного регулирования выходных координат двигателя. Сопротивления обмоток приняты для нагретого состояния двигателя. Модель электропривода содержит: источник питания, представленный звеном постоянного тока (ЗПТ); автономный инвертор напряжения (АИН), содержащий трехфазный транзисторный мост по схеме Ларионова; систему управления инвертором (СУ АИН), формирующую импульсы управления транзисторами (VT1…VT6); систему управления электроприводом (СУЭП), состоящую из наблюдателя потока (Flux_looker), и наблюдателя скорости (Speed_looker), формирующую управляющие напряжения UAy, UBy, UCy = л/3Uф/Udc (о.е.) и реализующую векторный полеориентированный закон управления; асинхронный двигатель (АД); датчики напряжения и тока (ДН_abс, ДТ_abc); блок формирования нагрузки (БФН), который в зависимости от сигнала управления Uy формирует постоянный момент сопротивления на валу АД,

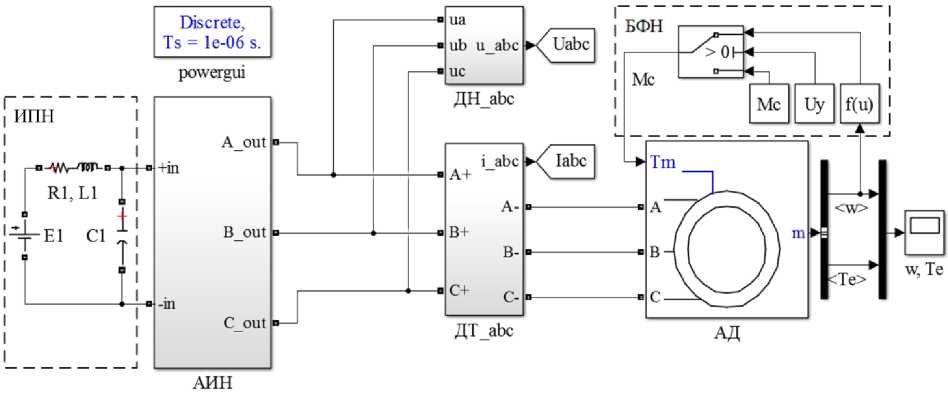
Рис. 2. Схема модели привода с АИН и АД

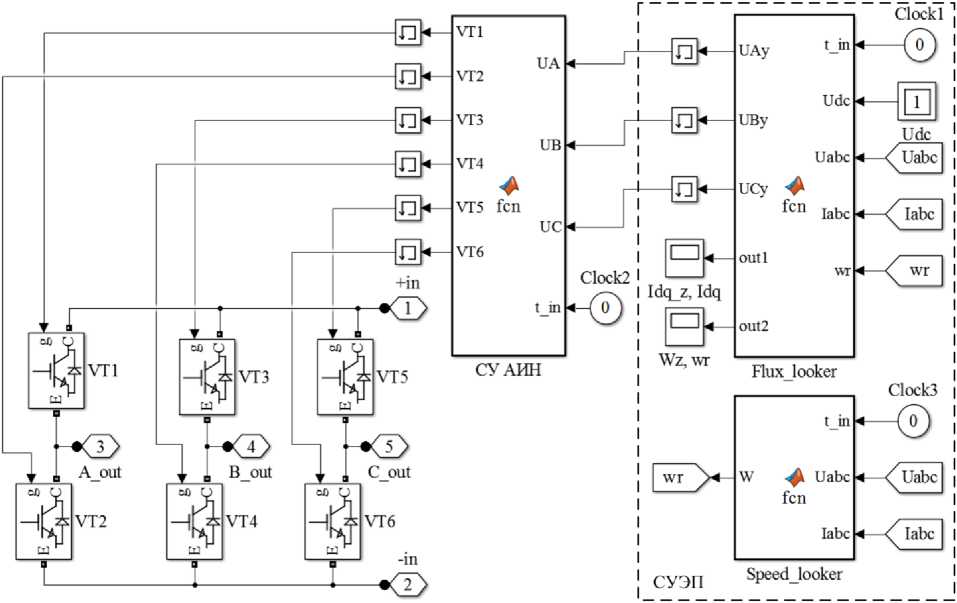
Рис. 3. Схема блока АИН

Электромеханические системы л иб о мом е нт с опрот ивл е н ия пропорци о на л ьн ы й квадрату скорости.

В данной работе рассматривается вопрос электромеханической совместимости преобразователя с двигателем в установившемся режиме работы, а именно влияние несинусоидальности выходного напряжения инвертора на пульсации электромагнитного момента двигателя, поэтому для упрощения расчетов первичный преобразователь не рассматривается, а напряжение питания инвертора принято идеально сглаженным и представлено источником постоянного напряжения E1 c индуктивностью L1, активным сопротивлением R1 и током I1.Напряжение питания АИН 550 В. Исследования выполнены при номинальных параметрах двигателя: напряжение питания 380 В, 50 Гц, мощность 20 кВт, коэффициент мощности 0,415, скольжение 4,15 %, индуктивность рассеяния статора 3,35 мГн, индуктивность намагничивания 8,58 мГн, индуктивность рассеяния ротора 2,23 мГн, активное сопротивление статора 0,0712 Ом, активное сопротивление ротора 0,1175 Ом, КПД = 0,775, индуктивность сглаживающего дросселя 220 мкГн, емкость фильтрового конденсатора 30 мФ.

Исследование электромеханической совместимости асинхронного электропривода

На компьютерной модели привода был выполнен ряд численных экспериментов, в результате которых рассчитаны пульсации электромагнитного момента АД. Производилась оценка пульсаций электромагнитного момента в зависимости от момента сопротивления (M c ) на валу АД при разных значениях частоты ШИМ инвертора и номинальной частоте вращения двигателя, а также при частотном регулировании скорости двигателя и моменте сопротивления вентиляторного типа.

Результаты исследований представлены на рис. 4 и 5, а также сведены в табл. 1 и 2 для несущей частоты 2 кГц.

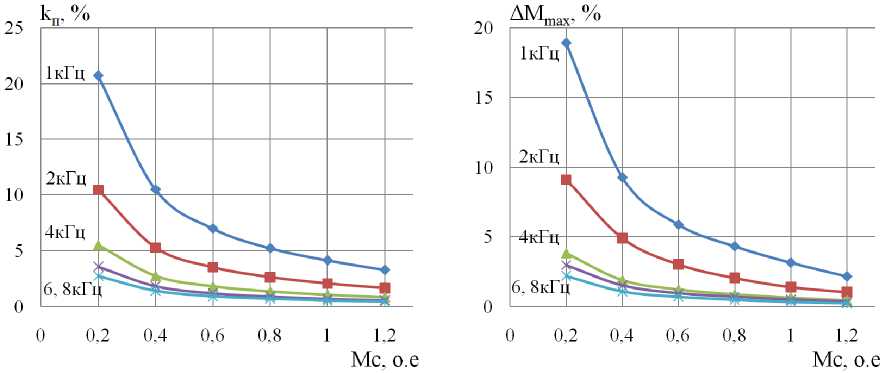
а)

б)

Рис. 4. Зависимости коэффициента пульсаций (а) и максимальной амплитуды пульсаций (б) электромагнитного момента АД от нагрузки на валу М_с

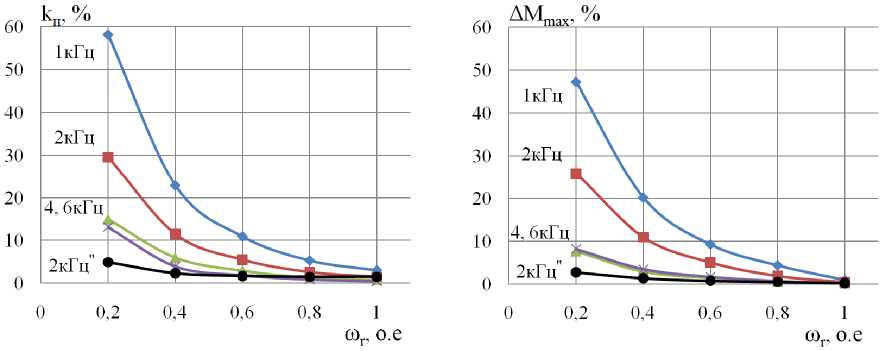
а)

б)

Рис. 5. Зависимости коэффициента пульсаций (а) и максимальной амплитуды пульсаций (б) электромагнитного момента АД при частотном регулировании скорости АД

Татаринов Д.Е., Козярук А.Е.

Таблица 1

Результаты расчета пульсаций электромагнитного момента в зависимости от М_с при f_ШИМ = 2 кГц

w r , o.e.	M с , o.e.	K м	k п , %	ΔM max , %
1	0,2	1	10,46	9,12
	0,4		5,26	4,9
	0,6		3,51	3,02
	0,8		2,62	2,05
	1		2,06	1,4
	1,2		1,64	1,03

Таблица 2

Результаты расчета пульсаций электромагнитного момента при частотном регулировании скорости АД при f ШИМ = 2 кГц

w r , o.e.	M с , o. e .	U DC = const			U DC = var
		K м	k п , %	ΔM max , %	K м	k п , %	ΔM max , %
0,2	0, 043	0,2	29,53	25,8	1	4,91	2,76
0,4	0,17	0,4	11,47	10,9		2,29	1,39
0,6	0,38	0,6	5,49	5,02		1,67	0,778
0,8	0,66	0,8	2,6	1,85		1,46	0,521
1	1	1	1,48	0,392		1,48	0,229

Рекомендации по обеспечению электромеханической совместимости электропривода

Как видно из рис. 4 и 5, а также представленных табличных данных, уменьшение момента сопротивления на валу АД приводит к возрастанию пульсаций электромагнитного момента двигателя в несколько раз, а увеличение частоты ШИМ инвертора позволяет их снизить. Соответственно, автоматическая подстройка частоты ШИМ инвертора на максимальную при уменьшении нагрузки на двигатель, и наоборот, когда нагрузка на двигатель высока – снижение частоты ШИМ (для экономии энергии), позволит снизить пульсации электромагнитного момента в 7…10 раз при малых нагрузках на валу АД, а вместе с тем уровень шума и вибрации двигателя.

Снижение пульсаций электромагнитного момента и следовательно, уровня шума и вибрации двигателя при частотном регулировании скорости позволяет осуществить подстройка напряжения звена постоянного тока преобразователя с целью поддержания постоянства коэффициента модуляции Kм = Uab /UDC при снижении частоты питания АД (зависимости 2 кГц" на рис. 5). Поддержание постоянства коэффициента модуляции при частотном регулировании позволило снизить пульсации электромагнитного момента ориентировочно в 2…10 раз.

В работе [7] проводилось исследование влия-

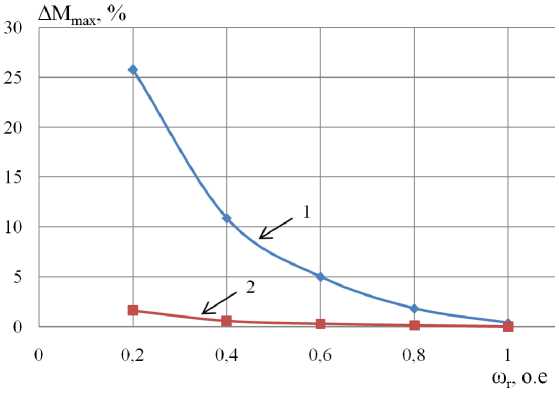
Рис. 6. Зависимости максимальной амплитуды пульсаций электромагнитного момента при постоянной частоте ШИМ 2 кГц (1) и переменной частоте ШИМ 1,5…2,5 кГц (2) от частоты вращения АД

Электромеханические системы

ние алгоритма с переменной частотой ШИМ на снижение высокочастотных пульсаций электромагнитного момента, в котором частота ШИМ инвертора изменялась по периодическому закону. Недостатком такого метода являлась возможность возникновения частотного резонанса при совпадении периода изменения частоты ШИМ в заданном диапазоне частот с периодом питающих двигатель токов, сопровождающаяся сильным увеличением пульсаций электромагнитного момента.

В данной работе предлагается изменять частоту ШИМ инвертора по случайному закону с равномерным распределением. Результаты исследования пульсаций электромагнитного момента при постоянной и переменной частоте ШИМ инвертора представлены на рис. 6.

Применение алгоритма с переменной частотой ШИМ позволило снизить амплитуды высокочастотных пульсаций электромагнитного момента ориентировочно в 10…15 раз, распределяя их по спектру [7].

Заключение

Результаты представленных исследований показывают возможность обеспечения электромеханической совместимости средствами управления электропривода, а именно снизить коэффициенты нелинейных искажений тока и напряжения инвертора, а также уровень пульсаций электромагнитного момента двигателя.