Алгоритмические основы исследования электромагнитных процессов в электроприводе герметичной задвижки

Исследование выполнено за счет гранта Российского научного фонда № 24-29-00089

Развитие отечественной энергетической инфраструктуры предполагает освоение ряда перспективных территорий, перечисленных в Указе № 296 «О сухопутных территориях Арктической зоны Российской Федерации» и дополнении к нему. Отличительной особенностью этих зон является не только сложный климатический режим, подробный анализ которого приведен в материалах государственного доклада «О состоянии и об охране окружающей среды Российской Федерации», но также удаленность и труднодоступность технологических объектов добычи в первую очередь нефтегазового сырья, требующих развитой системы магистральных трубопроводов. Протяженность отечественных трубопроводных систем, по которым перекачивается не менее 90 % всех добываемых нефтегазовых ресурсов, составляет более 250 тыс. км, из которых порядка 70 тыс. км без учета введенных в эксплуатацию в 2023 году используется для транспорта нефти и нефтепродуктов [1]. Эксплуатируемые трубопроводные магистрали состоят из технологических модулей, включающих запорные элементы, расстояние между которыми достигает 30 км. Возникновение аварийных ситуаций на удаленных участках трубопроводов приводит к выбросам перекачиваемого сырья, что представляет большую опасность для окружающей среды, а в некоторых случаях приводит к необратимым последствиям [2]. По причине удаленности поиск места аварии и доставка до него оперативно-технического персонала может занимать неопределенное время, это также относится и к участкам трубопроводов, проходящих под водой. Отдельным фактором, подтверждающим актуальность рассматриваемой проблемы, являются произошедшие 26 сентября 2022 года массовые утечки газа вследствие разрушения части международных подводных газопроводов.

Очевидно, что создание автоматических приводных устройств, обеспечивающих в случае утечки оперативную локализацию места повреждения, является актуальной задачей. Своевременное устранение на основе постоянного мониторинга процессов повреждений, обусловленных техническими и антропогенными факторами, снижает прямой экономический ущерб, составляющий порядка 1,5 млрд. руб. в год, но, что в условиях Арктической зоны особенно важно, ограничивает воздействие продуктов транспортирования на окружающую среду. В настоящее время электропривода находят практическое применение в различном технологическом оборудовании, начиная с миниатюрных механизмов, например, привод клапана блока терморегулирования системы жизнеобеспечения человека в условиях сверхнизких температур, заканчивая силовыми установками для перемещения крупногабаритных объектов. При этом почти в 50 % из эксплуатируемых электротехнических комплексов используются привода с линейным перемещением исполнительного механизма [3].

Проведенный авторами анализ показал, что в условиях Арктической зоны существующие привода не полностью удовлетворяют требованиям надежности, в частности вследствие конструкционной сложности. Повышение надежности приводных механизмов линейного перемещения при обеспечении требуемых усилий и переме- щений может рассматриваться как одно из приоритетных направлений увеличения эффективности объектов энергетического комплекса. Актуальность исследования также подтверждается информацией о существующих системах электропривода возвратно-поступательного движения на базе электромеханических преобразователей, показывающей заинтересованность производителей и потребителей энергетического оборудования в его дальнейшей модернизации и совершенствовании с целью улучшения технико-экономических характеристик [4-12].

Задача разработки электроприводов, адаптированных к условиям низких температур и характеризующихся высокой надежностью, может быть решена с использованием результатов, полученных авторами при создании теплогенерирующих перекачивающих устройств на основе электромеханических преобразователей. В данной статье приведен алгоритм проектирования и исследования электромагнитных процессов в приводном устройстве герметичной задвижки, а также примеры его реализации.

Материалы и методы

Состояния проблемы создания высоконадежных электроприводов показывает, что научные исследования в данной области ведутся во всех промышленно развитых странах [13-19].

Российскими учеными опубликовано достаточно много результатов, полученных при анализе эксплуатационных режимов электромеханических приводов для задвижек в нефтегазовой промышленности. Наиболее значимыми работами в данной области являются публикации А.Г. Гарганеева, А.С. Каракулова, А.И. Удовиченко, О.В. Потетенко, Н.Г. Шевченко, Е.С. Коваль, А.О. Смирнова, Н.И. Куракина, Р.А. Мышко, Г.В. Кулинченко и ряд других.

В статье [5] приводится экспериментальная оценка эффективности привода запорной арматуры на основе асинхронного двигателя с короткозамкнутым ротором с редуктором и безредукторного синхронного двигателя с вращающимся ротором. Авторами разработаны две модели привода на основе приведенных типов двигателей, протестированы методы оценки эффективности в реальном времени и получены данные для оценки энергоэффективности привода в процессе позиционирования. При использовании асинхронного двигателя в приводе запорных арматур наблюдается снижение его коэффициента полезного действия (КПД) с 60 % до 22 % (с учетом КПД редуктора). Применение синхронного двигателя связано со сложностью конструкции, трудностью пуска и регулирования скорости.

Сравнение типов редукторов (волнового, планетарного, червячно-колесного) по показателям «выходной крутящий момент/масса» применительно к мехатронным системам трубопроводной арматуры сделано в статье [6]. По мнению авторов, преимуществом редукторов червячно-колесного типа является естественная статическая самоблокировка. Таким же преимуществом обладает и винтовая пара. Авторы также отмечают, что невозможно однозначно сказать, какой тип привода выбрать в данном конкретном случае, они делают заключение, что по показателям веса, габаритов и цены невозможно спроектировать электропривод без редуктора, способный развивать крутящий момент аналогичный электроприводу с редуктором.

В работе [7] рассмотрены электродвигатели для бесступенчатого привода запорных арматур на базе различных электродвигателей, в том числе и с постоянными магнитами. Отмечено, что процесс пуска электродвигателя с большим пусковым моментом является сложной научной и практической проблемой. Такой режим возникает, например, в момент открытия заслонки трубопровода, когда на нее оказывается максимальная нагрузка. Оптимальным решением, по мнению авторов, является использование привода, содержащего асинхронный двигатель и редуктор, работающего с частотой вращения вала 10…120 об/мин.

Анализ имеющихся работ показывает, что создание приводов, непосредственно ориентированных на экстремальные температурные условия в большинстве публикаций не рассматривается.

Подробное описание конструкции привода герметичной задвижки, рассматриваемой в данной статье, приведено в работах [20, 21]. Информация о непосредственном приводе герметичной задвижки на базе асинхронного двигателя с интегрированным механизмом «винт-гайка» приведена в [21]. Авторами показано, что использование электромеханического преобразователя с линейным перемещением исполнительного элемента в качестве привода герметичной задвижки является перспективным вследствие существенного упрощения Ким К.К., Иванов С.Н., Азимов Х.Х.

АЛГОРИТМИЧЕСКИЕ ОСНОВЫ ИССЛЕДОВАНИЯ ЭДЕКТРОМАГНИТНЫХ ПРОЦЕССОВ В ЭЛЕКТРОПРИВОДЕ ГЕРМЕТИЧНОЙ ЗАДВИЖКИ конструкции, что обеспечивает высокую надежность и экологическую безопасность трубопроводной системы. Адаптация конструкции привода для низких температур обеспечивается электропроводящим герметизирующим элементом, выполняющим функции дополнительного теплового источника.

Оценка выполнимости привода герметичной задвижки с учетом влияния герметизирующего элемента, представляющим собой короткозамкнутую неподвижную обмотку, может быть сделана на основе алгоритмического и математического исследования и анализа эффективности преобразования электромагнитной энергии в механическую с учетом эксплуатационных условий. Теоретическую базу исследования наряду с традиционными методиками проектирования, разработками в областях электро-, термо- и гидродинамики, составляют методы автоматизированного проектирования, инженерного анализа и статистическое планирование эксперимента. Выбор в качестве силового элемента привода асинхронного двигателя с герметичным статором и короткозамкнутым ротором со встроенным элементом «винт-гайка» позволяет использовать математические модели, реализованные на основе теории обобщенного электромеханического преобразователя энергии.

На начальном этапе с использованием технологии построения виртуальных трехмерных моделей создается геометрическая форма объекта исследования, которая обеспечивает гибкую параметризацию и возможность учета определяющих факторов, влияющих на эксплуатационные характеристики привода.

Реализация системного подхода включает поэтапное решение задачи исследования путем построения трехмерной параметрической модели привода герметичной задвижки, увязки форм и размеров сопрягаемых элементов, полного описания геометрической формы, вариативное проектирование исследуемого устройства. Для разработки и анализа параметрической модели, обеспечивающей реализацию алгоритма исследования электромагнитных процессов, использованы методы твердотельного проектирования. Для определения значимых проектных параметров в алгоритме может быть предусмотрен блок планирования вычислительного эксперимента с использованием статистической обработки и анализа данных на базе критериев оптимизации проектных параметров комплекса при переменном векторе внешних возмущений. Проведение вычислительного эксперимента для нахождения характеристик потоковых процессов реализуется численными методами инженерного анализа, что обусловлено нелинейностью математических моделей. Принятие решения о завершении задачи исследования осуществляется сравнением результатов вычислительного и натурного экспериментов. Физическая реализация исполнительной части привода, необходимая для проведения экспериментальной верификации данных имитационного моделирования, осуществляется быстрым прототипированием.

Структурно электропривод герметичной задвижки рассматривается как сложная иерархическая модель, состоящая из алгоритмически упорядоченных элементов, раздельно выполняющих целевые задачи, но при этом охваченных централизованными глобальными связями.

Стратегической основой исследования и реализации такой модели на системном уровне является алгоритм ее функционирования и определяющие критерии: количественная оценка эффективности выполнения приводом целевой функции – перемещение исполнительного элемента на заданное расстояние с требуемой скоростью в условиях реального нагружения.

Исследование электромагнитных процессов является частью общего алгоритма проектирования привода с учетом тепловых, механических и гидравлических составляющих в задвижке, который приведен на рис.1.

Концептуально проектирование рассматривается как синтез структурной схемы и обоснование выбора ее элементов на основе глобального алгоритма, реализующего выполнение целевых функций, отражающих мультифизический технологический процесс. Для его реализация необходима информации о функциональных возможностях и принципах работы объекта исследования. Под «мультифизич-ностью» понимается одновременность протекания и взаимовлияния электромагнитных, механических, тепловых и гидравлических процессов.

Результаты

Параметрическая модель асинхронного двигателя с привязкой герметизирующего элемента к внутренней расточке корпуса статора, являющегося базовой деталью, выполненная в системе проектирования T-Flex CAD, приведена на рис.2.

Ввод результатов моделирования процессов течения жидкости в задвижке в пакете Flow S iniLlaticn

т

Тяговое усилие. скорость перемещения заслонки, приближенное значение КГЦ винтовой передачи.

Определение скорости перемещения заслонки еление мощности двигателя |

6 Расчет магнитной сели.

* Параметры рабочего релизе.

8 Ра счет пот ерь.

9 Ра счет рабочих характери стик

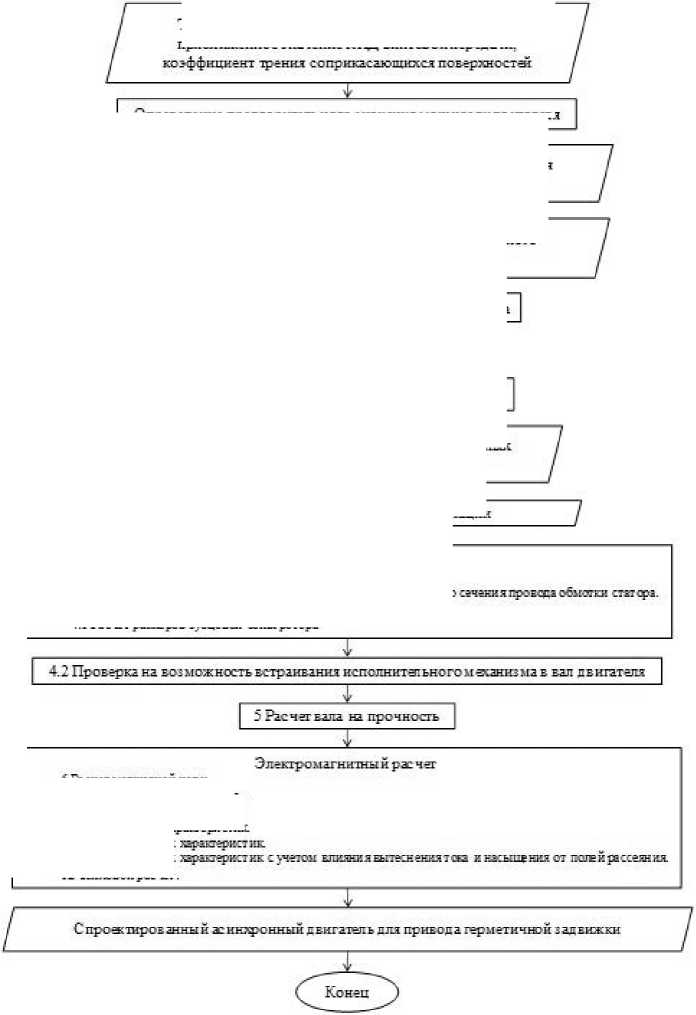
Рисунок 1. Общий алгоритм проектирования привода задвижки

Определение предварительного значения мощности двигателя Jr

О пр ед еление во s хюж ны х нохгиналь ны х с коростей д в игатеп я для предварительно рассчитанной мощности

О ц>ед еление диаметра и шага резьбы исполнительного механизма с помощью S ohd Works Simulation

;

Определение необходимого пускового момента

Сое тавл ение свод нон таблицы всех воз мож ных комбинации параметров механизма

Выбор наиболее подходящей комбинации

Эл ектромагнктны и расчет 1 Вьбор шавных размеров.

3 Расчет раз ie ров зубцовой зоныстзторзи возг-иного зазора.

4.1 Ра счет размеров зхбцовсн зоны ротора

12 ТЕПЛОВОЙ р»:Ч5Т.

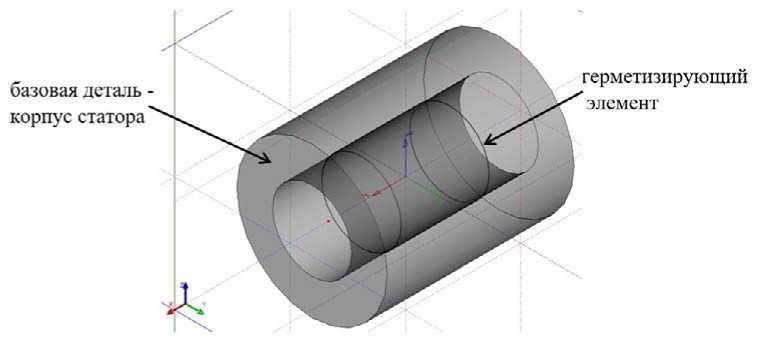
Рисунок 2. Позиционирование герметизирующего элемента в корпусе статора

При исследовании электромагнитных процессов в построенной геометрической модели с целью оценки влияния герметизирующего элемента на характеристики привода, требуется учесть следующее:

• -    наличие элемента из немагнитного материала увеличивает зазор между статором и ротором;

• -    способ непосредственного охлаждения ротора не связан со статором.

• -    для уменьшения потерь на трение ротора с жидкостью и потерь в герметизирующем элементе целесообразно обеспечить соотношение длины активной части l _t к полюсному делению τ не меньше 2;

• -    короткозамкнутый ротор выполнен с полым валом;

• -    пазовые клинья исключают деформации герметизирующего элемента от внутреннего давления в нем.

Герметизирующий элемент рассматривается в виде тороидальной короткозамкнутой обмотки, соответственно схема замещения электромеханического преобразователя для одной фазы включает параметры трех обмоток: статора, ротора и герметизирующего элемента. Очевидно, что последний будет препятствовать прохождению магнитного поля в ротор вследствие индуцированных вихревых токов, значения которых обусловлены физическими характеристиками элемента [22-25]. Результаты моделирования, полученные в программе ANSYS и приведенные на рис.3, показывают, что точная оценка эффекта влияния герметизирующего элемента невозможна вследствие неравномерного распределения в нем плотности вихревых токов (рис. 3: l _t – длина элемента; l _b – длина вылета, определяемая длиной лобовых частей обмотки; материал - бронза).

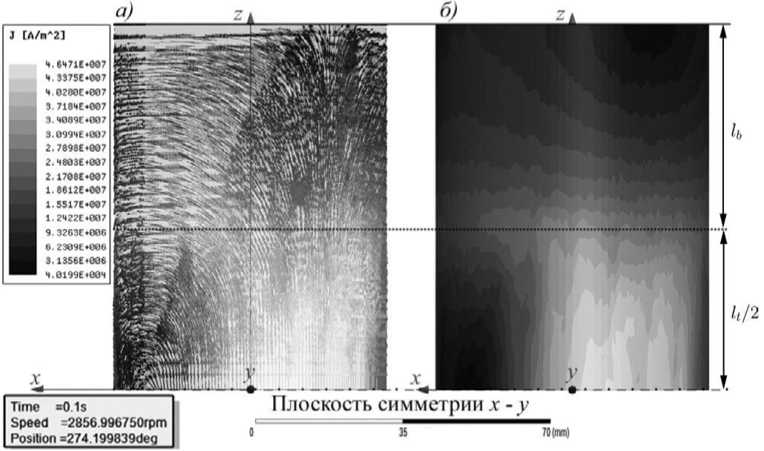
Рис. 3. Распределение плотности тока в герметизирующем элементе: а) вектор плотности тока; б) модуль плотности тока

Для математической формализации привода герметичной задвижки использовано описание в виде системы пространственных векторов [26].

В математической модели с синхронно вращающейся системой координат, реализованной с векторным представлением переменных, входные величины описываются сигналами постоянного тока, которые изменяются только в переходных режимах. Пространственный вектор вращается с частотой w ₀ и является управляющим. Модель включает матрицы-столбцы фазных напряжений, связанных токов и потокос-цеплений, в симметричном режиме токов нулевой последовательности нет, учитывается одна фаза двигателя.

Уравнения связи потокосцеплений и токов:

(^HiiKhi + l/^WiW^^(V^H^llOl) + I^IOl) + И'2хКЧ>;

№М^Х1|01) + Kx2|01) + |^х|01>, где |L,|,| L2|, |Lx| - матрицы индуктивностей, определяемые выражениями:

	^тф "*" ^la	- 2 ьтф	___ г          " 2 ьтф
и=	2 ьтф	^тф + Lia	2 ьтф >
	.   2 Ь^Ф	2	^тф "*" Lia
	^тф ”*" ^2a	2 ^тф
[■^2]=	2 ьтф	^тф + 1*20	2 ьтф
	.     2 ^,(!Ф	2 ьтф	^тф "*" L2a_
	^тф ”*" I^xa	2 ^тф	2 ьтф
[LJ =	2 ^?пф	^тф + Lxa	2 ^?пф
	_   2 ^тф	2 ^тф	^тф + Lxa

В описании модели использованы следующие обозначения: мгновенные значения напряжений статора - u_1A, u_1B, u_1C ; мгновенные значения токов в фазных обмотках статора, ротора, герметизирующего элемента соответственно - i_1A, i_1B, i_1C, i_2a, i_2b, i_2c, i xA^xB^xC i полные потокосЦепления тех же обмоток — Ф^, ^ ^ ic, ^ W_2y ^ 2c , ^ ^ ^ xc J активные сопротивления и собственные индуктивности обмоток - R 1 , R 2 , R_x; L 1 , L 2 , L x ; индуктивности обмоток, обусловленные наличием потоков рассеяния, - L_1σ, L_2σ, L_xσ ; потокосцепление и индуктивность намагничивающего контура - V m , L m ; угол поворота ротора - γ ; коэффициент рассеяния - σ .

Система уравнений с использованием пространственных векторов во вращающейся системе координат имеет вид:

Vi - RJy 4    + 7wov tp о = R^h + V + ^W24 2'

—* дф *       ---*

\ 0 — R_YI_Y 1--- + JWnH^,

4’1 — Т^/^ 4- А_т/г "*" L_mI_xl ^*2 ^— ^тЛ + ^2^2 + L_mI_x, хЧ^ L_mIy 4- L_ml₂ 4- L_xl_x.

В (1) внешними управляющими воздействиями являются не только составляющие пространственного вектора ^ , но и частота, поэтому необходимо преобразование в систему, связанную с вектором . Пространственный вектор в комплексном виде при совмещении действительной оси с α , а мнимой - с β :

^2 = V2u+jV2b.

Для согласования систем координат необходимо выполнение условия:

Ψ 2b=0.

Уравнение электрического равновесия применительно к ротору имеет вид:

о = Rih +-^+JW₂^₂       ~^ = -R₂t_2a; W_o=^- + p_nw. (2)

Вектор намагничивающего тока:

Im — 1г + ^2 + lx-

С учетом уравнений (2) система (1) принимает вид:

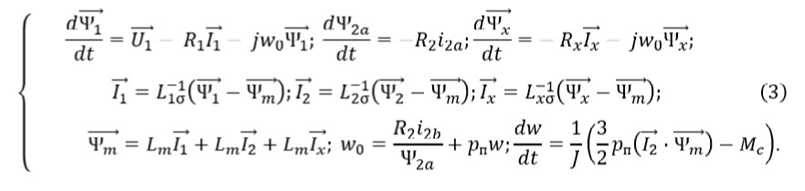
Система уравнений (3) содержит уравнение движения, обусловленного взаимодействием тока и потокосцепления , и учитывает моменты инерции J и нагрузки M_c , включающие приведенную массу шибера и потери трения в задвижке [21]. Модель позволяет учесть изменение насыщения магнитной цепи за счет коэффициента связи основного магнитного потока и намагничивающего тока, соответствующего ненасыщенной машине с постоянными индуктивностями рассеяния L_1a,L_2a,L x_o :

^L = ^L . +k . W к; ^L = ^L +k . W к; ^Lx= ^L x _a ⁺ k . W ^L m ^.

Обсуждение

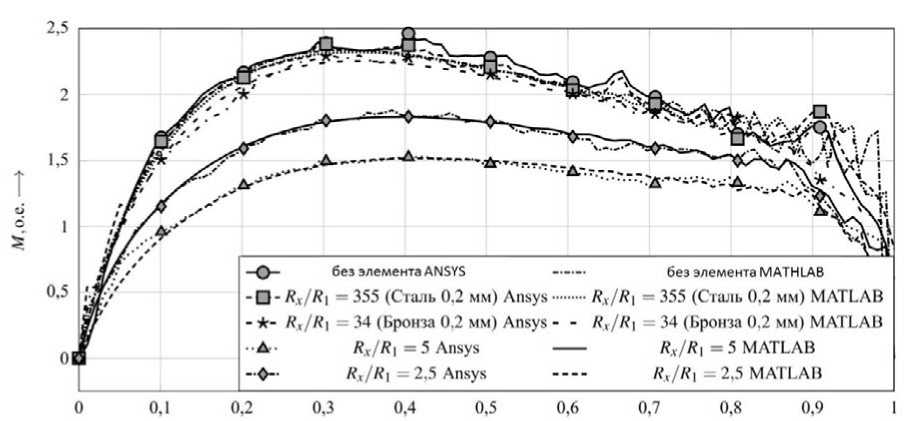
Механические характеристики электропривода герметичной задвижки, формализуемого системой (3), выполненные в разных программных средах приведены на рис.4. В качестве базового варианта для расчета выбран общепромышленный асинхронный двигатель, номинальные параметры которого приведены в таблице 1. Момент трения на шибере предварительно имеет линейный характер, определяемый коэффициентом трения 0,36 (латунь-латунь).

s.o.e. —►

Рисунок 4. Механические характеристики электропривода герметичной задвижки

Таблица 1.

Технические данные

Мощность Р 2н, кВт	30
Линейное напряжение U , В	380
Ток фазы І фн, А	191
Частота питания f , Гц
Момент двигателя М н, Н	61
Частота вращения w о, с-1	25
Число полюсов 2 р п	4
КПД (с учетом герметизирующего элемента), %	75
Коэффициент мощности, %	80
Момент инерции ротора с учетом шибера J , кг·м2	0,25
Скольжение s н, o.е.	0,16

Анализ полученных результатов показывает, что основное влияние герметизирующего элемента на электромагнитный момент связано с его активным сопротивлением R_x . Увеличение относительного сопротивления элемента R_x / R₁ (R₁ – активное сопротивление фазной обмотки статора) приводит к разнотемповому возрастанию номинального, пускового, критического моментов. Индуктивное сопротивление необходимо учитывать только при R_x/ R₁< 2 . Теоретически при R_x → ∞ и Lx → 0 энергетические характеристики привода задвижки приближаются к характеристикам привода при отсутствии между статором и ротором герметизирующего элемента. При соотношении R_x/ R₁>100 снижение КПД не превышает 3 %.

Заключение

Создание новых типов автономных силовых приводов линейного перемещения на базе специальных электромеханических устройств с учетом удаленных эксплуатационных факторов позволяет повысить эффективность критических объектов инфраструктуры энергетического комплекса. Рассмотренный алгоритм исследования электромагнитных процессов в электроприводе герметичной задвижки на основе его описания системой пространственных векторов позволяет учесть влияние определяющих параметров на эффективность работы устройства. Математическая модель, полученная на основе векторного описания входных и выходных переменных, а также внешних и внутренних возмущений, позволяет учесть нелинейность коэффициентов, связанных с определяемыми активными сопротивлениями, индуктивностями, взаимными индуктивностями. Оценка влияния размерных соотношений, встроенных в геометрическую модель, создает возможность последующей трехмерной оптимизации основных элементов привода и задвижки с учетом тепловых и гидродинамических процессов в магистрали. Это позволяет не только обеспечить заданный технологический режим, но и устойчивость системы в условиях низких температур за счет утилизации тепловыделений в герметизирующем элементе.