Алгоритмическое и программное обеспечение параметрического синтеза электромеханических структур с магнитной коммутацией

Практика проектирования электромеханических преобразователей (далее – ЭМП) представляет собой чередование решения задач анализа и синтеза для достижения таких целей, как максимальная эффективность и низкая стоимость с одновременным снижением массы активных материалов [1; 18]. Специалистов и исследователей привлекает надежность, технологичность и возможность преобразования конфигураций при конструировании машин с магнитной коммутацией для различных применений [2; 15; 16]. Математическая модель основной задачи нелинейного программирования, охватывающая проектирование ЭМП, может быть представлена в следующем виде [6; 12]:

F ( X i , X 2 ,..., X p ) = min;

G i ( X i , X 2 ,..., X p ) > 0;

G 2 ( X i , X 2 ,..., X p ) > 0;

— . — . — . — . — . — . — . — . — . — .

G m ( X i , X 2 ,..., X p ) > 0;

X i > 0; i = 1,2,..., p .

Содержанием математической модели применительно к проектированию ЭМП является нахождение совокупности параметров X= ( X 1 , X 2 ,...,X P ) , обеспечивающих экстремальное значение целевой функции F ( X 1 , X 2 ,...,X P ) = min при ограничениях G m ( X 1 , X 2 ,_,X P ) > 0 .

Проектирование ЭМП сводится к многократному расчету зависимостей между основными показателями, заданных в виде системы формул, эмпирических коэффициентов, графических зависимостей, которые можно рассматривать как уравнения проектирования [8; 17].

Целью исследования является разработка алгоритмов и программных кодов на языке программирования высокого уровня для решения задач комплексного параметрического синтеза при эскизном проектировании ЭМП с магнитной коммутацией (далее – ЭМПМК), отличительной особенностью которых являются сосредоточенные электрические обмотки при распределенной магнитной системе, что приводит к необходимости построения индивидуальных расчетных моделей и программ.

В качестве параметра оптимизации рассматривается мощность, приходящаяся на единицу массы активных материалов меди и стали. В этом случае оптимум целевой функции связан с ее максимумом и отвечает задаче получения ЭМПМК, отличающихся повышенной удельной мощностью [11].

Материалы и методы

Для достижения поставленной цели разработан комплексный метод параметрического синтеза, основанный на сочетании оптимизационной процедуры по результатам численного эксперимента, с синтезом в направлении от электромагнитных нагрузок к геометрическим размерам машины. Дальнейшая процедура комплексного параметрического синтеза демонстрируется на примере модульной синхронно-реактивной индукторной машины с электромагнитным возбуждением. Входными величинами являются электромагнитные нагрузки, а выходными – геометрические размеры машины и уровень параметра оптимизации [5; 9; 10; 13].

Процедура комплексного параметрического синтеза состоит из четырех этапов, на каждом из которых сужается область варьирования значащих факторов (см. Рисунок 1).

На первом, основном, этапе автоматизированная программа расчета реализует синтез по неполному набору данных в направлении от электромагнитных нагрузок к размерам ЭМПМК.

На втором этапе производятся численные эксперименты с определением параметра оптимизации на основе теории планирования экспериментов. В результате этого находится область варьирования электромагнитных нагрузок, которая близка к оптимальной.

На третьем этапе реализована статистическая обработка результатов численных экспериментов, а также определение значащих факторов, регрессионный анализ и модель оптимизации.

Четвертый этап оптимизационной процедуры построен на основе градиентного метода Бокса – Уилсона, сужающего зону варьирования значащих факторов, при которых параметр оптимизации удовлетворяет заданным условиям.

Алгоритмическое и программное обеспечение параметрического синтеза

Алгоритмическое и программное обеспечение относится к первому, основному, этапу комплексного параметрического синтеза ЭМПМК. Оно реализовано на базе объектноо-

Алгоритмическое и программное обеспечение параметрического синтеза ...

риентированной системы Delphi-5 на алгоритмическом языке Object Pascal. Выбор языка обусловлен тем, что этот императивный структурированный высокоуровневый язык программирования предназначен для написания прикладного программного обеспечения. Он имеет один из самых быстрых компиляторов с хорошим объектным кодом, обладает простотой и скоростью, не требует снабжения дополнительными библиотеками [3; 4; 7].

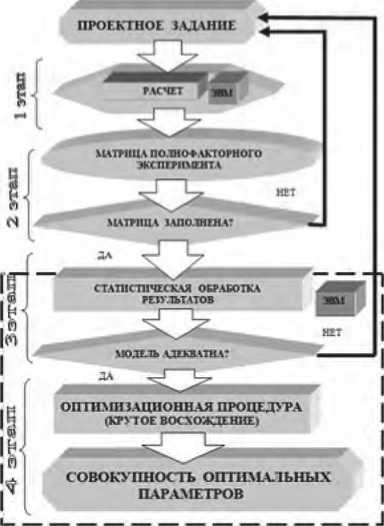
Рисунок 1. Процедура комплексного параметрического синтеза ЭМПМК

Алгоритм представляет собой заданную последовательность вычислительных процедур и самостоятельных программ в составе программных блоков (см. Рисунок 2), построенных на расчетных формулах, представленных в соответствующих методиках расчета [14; 19; 20].

Программа позволяет вводить и редактировать следующие три группы параметров, записанных в программных кодах.

• 1.    Номинальные параметры проектного задания: мощность S _н, кВА; напряжение U _н, В; частота f , Гц; коэффициент мощности cosφ, о.е.

• 2.    Независимые параметры из опыта проектирования: коэффициенты заполнения окна обмоткой возбуждения K _зв, о.е. и обмоткой якоря K _зр, о.е.; плотность тока в обмотках jР , А/м²; номинальное значение индукции в воздушном зазоре Вδ, Тл; индукции насыщения зубцов B _nas, Тл.

• 3.    Предварительные значения коэффициентов рассеяния Кσ и модуляции K λ магнитного потока, которые программа уточняет в рекурсивном режиме.

{процедура задания исходных параметров} procedure TForm1.FormCreate(Sender: TObject);

begin

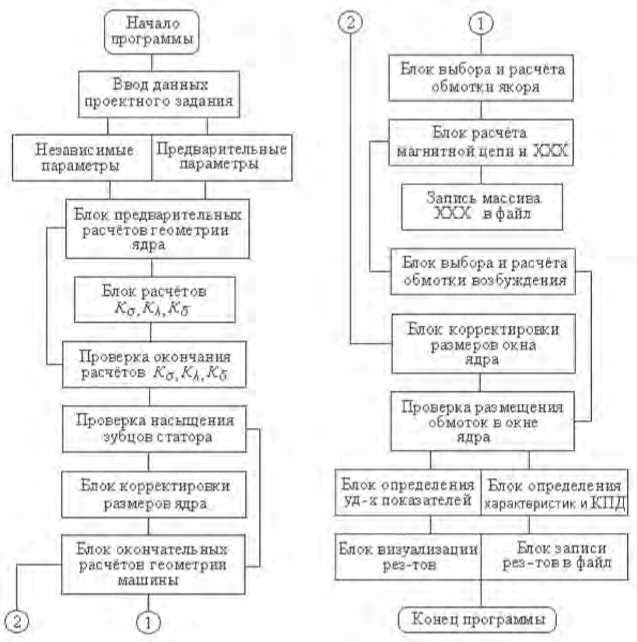
Рисунок 2. Алгоритм расчета ЭМП МК

При разработке программы особое внимание уделено удобству и наглядности ввода, редактирования и вывода данных. Ввод данных осуществляется изменением чисел в окнах редактирования экрана монитора с помощью стрелок вверх – «больше», вниз – «меньше» (см. Рисунок 3).

Алгоритмическое и программное обеспечение параметрического синтеза ...

Параметры. принимаемые предварите льмо

„                    Ke    h 1 Проектное задание            11 1       w | SH.KBAI”»    С|    НФ   I2     ±| Um В I750          Q     '°5 р.А/м2 18200000 2 1 1-Гц |450       5|              --------- . 1               |В,А/м2 12700000 п.об/с Н9        2 1 Кэр |0.55      v | cos fi I09 _ BdeW.Tn |0 6 n----- К лямбд h g Ub.B I220 ±j KF ^ 3 ' ^l.			Ксигм П"7 C I deNa.M I" v | Вмас.Тл I1-2	dla.rp   I85      2tj Se1.»2 l^7     C] Гам м  I8-9      C |
			Внач.Тл |0.3          | azf        |0 5        - | м2      |0 5       - | Сталь    |2 Ka      |11      C| Кмж     |09      C| Вком.Тл  I1 2       C I	Гамет pg    _2J СмГр |ю Сст.Гр |з T стали.гр|юо    u Исполн |l a1 I2      ±l
	Новые данные | [ Решение |	d ^Рорма 2 |    «Рорма 3 |	Форма 4 |   Форма 5 |	)скиэ машины | ЭскиэЭМя| График XK |

• Рисунок 3. Задание исходных параметров

В конце алгоритма в блоке визуализации реализуются результаты трех программ: «Кривая холостого хода» (см. Рисунок 4), «Эскиз электромагнитного ядра» (см. Рисунок 5), «Эскизный чертеж машины» (см. Рисунок 6).

В начале алгоритма в рекурсивном режиме работает блок предварительных расчетов геометрических размеров электромагнитного ядра, где уточняются расчетные коэффициенты K σ и K λ.

{Геометрические размеры электромагнитного ядра} tz1_n:=lz1_n/az1;

if ISP=2 then D1:=(tz1_n*(m*Z1+3))/pi else D1:=(tz1_n*Z1)/pi;

if ISP=2 then tz1_s:=pi*D4/(m*Z1+3)

else tz1_s:=pi*D4/Z1;mm1:=(tz1_n-lz1_n)/2;

M5:

После этого вступает в работу блок проверки насыщения зубцов статора, где проверяется значение магнитной индукции в зубцах статора и сравнивается с заданным значением В _нас. При этом корректируется сечение зубцов, размеры электромагнитного ядра, снова уточняются коэффициенты K σ и K λ, и окончательно определяются размеры электромагнитного ядра.

Далее вступает в работу блок выбора и расчета обмотки якоря, где исходя из напряжения, плотности тока, числа параллельных ветвей и сечения провода определяются: число витков в фазе и параллельной ветви, сечение провода без изоляции и с изоляцией. В заключение определяется площадь окна электромагнитного ядра, занимаемая круглыми изолированными проводами.

{Выбор обмотки статора}

M12:

AFmax:=AFz2;AFmin:=AFmax/Klamd;dAF:=AFmax-AFmin;

{Диаметр голого провода статора} dc:=Sqrt((4*Sc)/pi);

{Диаметр изолированого провода статора} dcu:=dc*1.12;

{Площадь окна, занимаемая круглыми проводами статора в одном модуле}

Sck:=Sqr(dcu)*Wp_1;

В блоке расчета магнитной цепи и характеристики холостого хода кривые намагничивания сталей В = μ (Н) заданы в аналитической форме. Исходя из начального значения индукции в зазоре программа с заданным шагом осуществляет расчет текущих значений индукции на различных участках магнитной цепи до заданного конечного значения B _кон. Определение напряженности Н по известным значениям индукции В для выбранной марки стали осуществляется по приведенному алгоритмув результате обращения к соответствующей процедуре.

После расчета текущих значений МДС и ЭДС они выводятся на экран монитора и печатаются в файл вычисления данных (см. Рисунок 4).

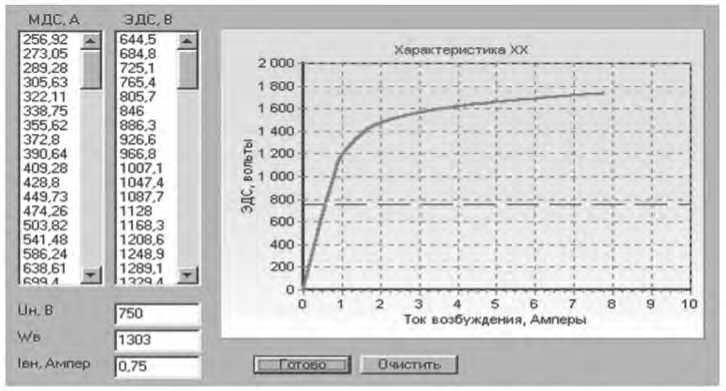
Рисунок 4. Характеристика холостого хода генератора

Код программы формы 2 (рисование характеристик холостого хода):

unit Unit8;

interface uses Windows, Messages, SysUtils, Classes,Graphics, Controls, Forms, Dialogs, StdCtrls, Menus, TeEngine, ExtCtrls, TeeProcs, Series, Chart;

type

Алгоритмическое и программное обеспечение параметрического синтеза ...

TForm8 = class(TForm)

Button1: TButton;

Label1: TLabel;

Edit3: TEdit;

Label5: TLabel;

procedureFormActivate(Sender: TObject);

procedure Button2Click(Sender: TObject);

private

{ Private declarations } public

{ Public declarations } end;

В блоке выбора и расчета обмотки возбуждения на основании определенной МДС и заданного напряжения определяются: сечение меди, число витков, ток возбуждения, диаметр провода без изоляции и с изоляцией. В заключение вычисляется площадь окна, занимаемая изолированными круглыми проводами обмотки возбуждения.

{Расчет обмотки возбуждения}

{Сечение меди обмотки возбуждения}

Sov:=(Fvn*lv*(1+0.004*dtv)*1E-6)/(57*Uv);

{Площадь окна, занимаемая круглыми проводами

ОВ и ОЯ в одном модуле}

{Площадь окна одного модуля}

M16:

После выбора обмоток программа осуществляет проверку размещения изолированных проводов обмоток в модуле окна электромагнитного ядра и при необходимости корректирует ее размеры (см. Рисунок 5), а затем выводит на экран монитора общее графическое изображение машины (см. Рисунок 6).

В блоке определения удельных показателей рассчитывается масса активных материалов электромагнитного ядра и его стоимость по ценам, которые задаются при вводе данных. На основании этих параметров производится вычисление удельных характеристик электромагнитного ядра: удельной массы по мощности G _я.м, кг/кВт; удельной мощности по массе Р _я.в, кВт/кг; удельной стоимости по мощности УЦ_ядра, руб/кВт.

В блоке определения КПД распложены три программы:

• •    программа определения сопротивлений электрических обмоток в функции температуры с учетом эффекта вытеснения тока;

• •    программа определения удельных потерь в функции индукции и частоты;

• •    программа расчета КПД с учетом потерь в меди обмоток и стали электромагнитного ядра.

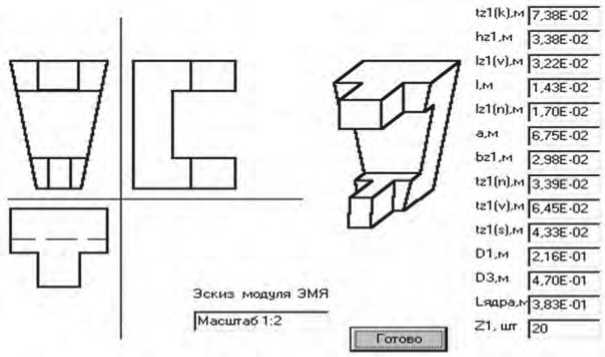
Рисунок 5. Эскиз модуля электромагнитного ядра

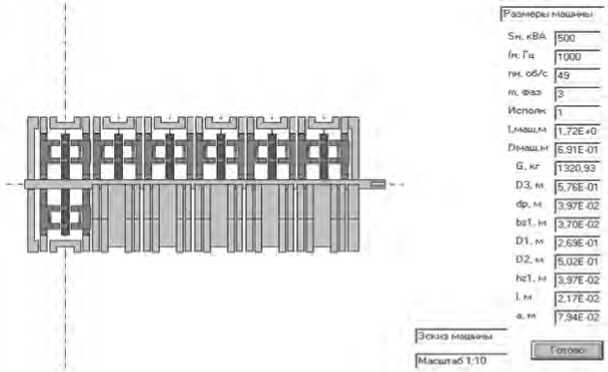
Рисунок 6. Графическое изображение продольного разреза

Код программы формы 7 (рисование эскиза машины).

unit Unit7; interface uses Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, TeEngine, Series, ExtCtrls, TeeProcs, Chart; type TForm7 = class(TForm)

Button1: TButton;

Edit1: TEdit;

Label16: TLabel;

procedureFormActivate(Sender: TObject); private

{ Private declarations } public

{ Publicdeclarations } end;

Алгоритмическое и программное обеспечение параметрического синтеза ...

По завершении работы программы, результаты расчетов заносятся в файл данных и визуализируются на экране монитора, а также осуществляется масштабное графическое изображение продольного разреза эскиза машины. Время решения одного варианта расчета составляет от долей секунды до десятка секунд.

Выводы

Необходимость разработки алгоритмического и программного обеспечения для решения задач параметрического синтеза электромеханических преобразователей с магнитной коммутацией, содержащих сосредоточенные электрические обмотки при распределенной магнитной системе, вызвана их конструктивной особенностью.

Полученные результаты алгоритмического и программного обеспечения ориентированы преимущественно на проектирование модульных синхронно-реактивных индукторных машин с электромагнитным возбуждением.

Результаты применения программного обеспечения позволяют принимать управленческие решения при выборе предпочтительных вариантов из полученного множества исходя из проектировочных заданий и энергетических, массогабаритных и стоимостных показателей электрических машин новых конструкций.

Полученные результаты могут найти применение в электромашиностроительной отрасли и будут полезны исследователям и проектировщикам, не имеющим достаточного опыта в разработке, для последующего комплексного параметрического синтеза машин подобных конструкций.