Алгоритмизация процесса обучения теории вероятностей в вузе

Одна из первых тем в курсе «Теория вероятностей и математическая статистика» – классическое определение вероятности события. Обычно, после прочтения задачи, у студента в голове возникает хаос, все сваливается в одну кучу: событие, исходы, вероятности. Структурировать рассуждения, помочь выстроить логическую цепочку из этих рассуждений помогает следующий алгоритм:

• 1.    Выяснить какой опыт имеет место в рассматриваемой задаче.

• 2.    Сколько существует у данного опыта возможных исходов ( n ).

• 3.    Ввести событие А , вероятность которого требуется найти в задаче.

• 4.    Сколько существует исходов, благоприятствующих этому событию ( m ). Тут тоже важно вслух сформулировать вопрос.

  
  
  

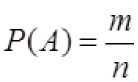
• 5.    Применить формулу классической вероятности

На данном этапе хорошо, когда студенты вслух формулируют вопрос.

На каждом этапе важно предлагать студенту сформулировать тот вопрос, на который требуется на этом этапе дать ответ. При этом следует добиваться от студента абсолютно четкого понимания того, что такое испытание (опыт, эксперимент), что такое событие, и что такое вероятность события.

Алгоритм решения на геометрическую вероятность таков:

• 1.    Выяснить какой опыт имеет место в рассматриваемой задаче. Так как число исходов опыта, описанного условием задачи, бесконечно, то для вычисления вероятности нужно воспользоваться геометрическим способом. Для этого опыт необходимо свести к выбору точки в некоторой области.

• 2.    Определить область G всех возможных исходов опыта и найти его меру (длину, площадь или объем) – mes G .

• 3.    Сформулировать событие А , вероятность которого требуется найти в задаче.

• 4.    Определить область Q , которая является подмножеством множества G и является множеством исходов, благоприятствующих событию А. найти меру множества Q – mes Q .

• 5.    Найти вероятность события А по формуле:        mesG

р(А-)=1^е

Решение задач на геометрическую вероятность вызывает много трудностей. Это связано именно с трудностью интерпретации сюжетной задачи как задачи на бросание точки на некоторую область. При этом преподавателю целесообразно не преподносить сразу студентам идею этой интерпретации, а с помощью серии вопросов спровоцировать появление верной идеи.

Для решения задач на применение теорем сложения и умножения рекомендуется следующий алгоритм:

• 1.    Сформулировать событие, вероятность которого требуется найти в задаче.

• 2.    Сформулировать события, через которые можно выразить искомое событие с помощью операций сложения, умножения и отрицания.

• 3.    Найти вероятности событий, сформулированных в пункте 2.

• 4.    Выразить искомое событие через события, сформулированные в п. 2, с помощью операций сложения, умножения и отрицания.

• 5.    Перейти к вероятности искомого события и применить теоремы сложения и умножения.

Следствием теорем сложения и умножения являются формулы полной вероятности и Байеса. Для этих формул можно предложить студентам следующий алгоритм:

• 1.    Сформулировать событие A , вероятность которого требуется найти в задаче (или, для формулы Байеса, то событие, которое произошло в результате опыта);

• 2.    Сформулировать гипотезы           ^ .

• 3.    Найти вероятности гипотез Р^Н^, P(H₂),...,P(H_lt .

• 4.    Сделать проверку Р(Н1)*Р(Н2)+... + Р(Нп) = 1.

• 5.    Записать    формулу полной    вероятности для данной

• 6.    Найти условные вероятности      . На этом этапе желательно, чтобы

• 7.    Подставить значения найденные в п. 3 и п. 6 в формулу полной вероятности (п. 5).

• 8.    Вычислить вероятность искомой гипотезы по формуле Байеса:

  

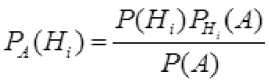
НН н

W^H)-?^

задачи          i=-                .

студенты хотя бы устно проговаривали вероятность какого события и при каком условии находят.

Для формулы Байеса добавляется еще один пункт:

Для задач, в которых происходит серия испытаний по схеме Бернулли, алгоритм таков:

• 1.    Сформулировать событие A , вероятность которого требуется найти в задаче.

• 2.    Составить схему Бернулли:

• 1.    сформулировать, что будем понимать под одним испытанием;

• 2.    определить количество испытаний n ;

• 3.    проверить являются ли испытания независимыми;

• 4.    разбить исход одного испытания на две группы: «успех» и «неудача». «Успех» = {исход, благоприятствующий событию А }, «неудача» = {исход, противоположный «успеху»};

• 5.    Найти вероятности «успеха» – p и «неудачи» – q . Следует убедиться, что p и q не изменяются от испытания к испытанию в данной серии испытаний.

• 3.    Выразить вероятность события А через вероятность m успехов

.

(т»й = С"1 г)тат^т rnV"4-^nP у или, в случае,

если количество испытаний велико, приближенные формулы:

если n велико и p очень мало ( Tip <   )   – формулу

Лте"

РЛ^т) =--- —_; Я = пр

Пуассона:           т.         ;

если n велико и p не очень мало ( пр >  ) – формулу Муавра- ч 1   / ч т-пр

Р(т) ®      ^(х), х =

Лапласа:         ■sjnpq          фрд .

Алгоритмизация процесса решения задач позволяет студентам четко представлять план решения задачи, анализировать условие, учит их аналитически, структурированно мыслить, логически рассуждать. Такой подход способствует более прочному усвоению знаний, более четкому и осознанному применению основных понятий и теорем теории вероятностей.