Алгоритмы быстрого расчета дифракции радиально вихревых лазерных полей на микроапертуре
Автор: Хонина С.Н., Устинов А.В., Волотовский С.Г., Ананьин М.А.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Физика и электроника
Статья в выпуске: 4-1 т.12, 2010 года.
Бесплатный доступ
Рассмотрены алгоритмы непараксиального векторного моделирования распространения ограниченных апертурой лазерных полей, основанных на интегральном преобразовании Релея-Зоммерфельда первого типа и разложении по плоским волнам. Проведено сравнение работы рассмотренных алгоритмов на примере дифракции вихревой конической волны на микроапертуре в ближней зоне. Показана эффективность предложенного алгоритма непараксиального векторного распространения на основе разложения по плоским волнам с учетом радиально-вихревой симметрии по точности и экономии вычислительных ресурсов.
Непараксиальные дифракционные операторы распространения, фазовая вихревая сингулярность, ближняя зона дифракции
Короткий адрес: https://sciup.org/148199350
IDR: 148199350 | УДК: 541.144
Текст научной статьи Алгоритмы быстрого расчета дифракции радиально вихревых лазерных полей на микроапертуре
В связи с уменьшением размеров оптических устройств, а также источников лазерного излучения, большое внимание последнее время уделяется описанию непараксиального распространения световых полей [1–9] и разработке алгоритмов моделирования такого распространения [10–21].
Непараксиальная модель, основанная на теории Релея-Зоммерфельда, позволяет получать согласующиеся с экспериментами результаты на очень близких расстояниях [22, 23]. Однако при уменьшении поперечных размеров светового поля (или его характерных деталей) до размеров порядка длины волны также необходимо учитывать векторный характер светового поля. В этом случае можно воспользоваться векторным вариантом интегралов Релея-Зоммерфельда [24, 2, 25] или методом разложением по плоским волнам [26, 27].
В первом случае сложно воспользоваться какой-либо симметрией световых полей, поэтому для упрощения расчетов или получения аналитических выражений приходится использовать аппроксимации [12, 28]. Во втором случае можно воспользоваться радиальной симметрией или разделением входного поля на радиальную и угловую составляющие и свести двумерные интегралы к одномерным [29, 30].
В данной работе проведено сравнение различных алгоритмов расчета дифракции радиально-вихревых лазерных полей на микроапертуре в приближении бесконечно тонкого идеально проводящего экрана.
Среди рассмотренных алгоритмов: непараксиальная аппроксимация дифракционных интегралов Релея-Зоммерфельда в векторной форме при радиально-вихревой симметрии; обобщение быстрого алгоритма вычисления интегрального преобразования Релея-Зоммерфельда для произвольных полей [21]; быстрый алгоритм, основанный на разложении по плоским волнам при радиально-вихревой симметрии, позволяющий применять преобразование Ханкеля [32] и реализация этого алгоритма для произвольных полей на основе быстрого преобразования Фурье (БПФ). Обсуждаются особенности реализации известных алгоритмов, а также достоинства, недостатки и область применимости предложенных.
1. НЕПАРАКСИАЛЬНАЯ СКАЛЯРНАЯ МОДЕЛЬ
Дифракция световой волны на отверстии в непрозрачном экране обычно описывается на основе теории Гельмгольца-Кирхгофа или Ре-лея-Зоммерфельда (в зависимости от граничных условий), а также с использованием разложения по плоским волнам (углового спектра).
Дифракционный интеграл Релея-Зоммер-фельда первого типа [33] в декартовых координатах имеет следующий вид:
ik l
E ( u , v , z ) = -— [J E X x , y )—
2 n v l
L 0
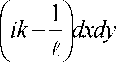
. (1)
где E 0 (x , y ) - входное поле, l = ^ (u - x) + ( v - y)2 + z 2, S 0 - область, в которой задано входное поле, k = 2 п / X — волновое число, l - длина волны.
Скалярный непараксиальный оператор распространения с использованием разложения по плоским волнам записывается следующим образом [34]:
EUVz ) = 72 f EXУ )
Л
^ 0
j J exp ( ikzхХ- Г -П ) exp ( ik Wl - x ) +n ( v - y ] ) d ^ d p' d x d У
где S S : g , < ^/ c 2 + p 2 < o 2 — область учитываемых пространственных частот. При о1 = 0, О 2 = 1 рассматриваются только распространяющиеся волны, а при о1 = 1, О 2 > 1 - только затухающие волны.
Вычисление выражения (2) может быть реализовано через БПФ [10, 17].
Для плоской освещающей волны, ограниченной круглой диафрагмой радиуса R , входное поле в (1) и (2) будет иметь следующий вид:
I 1, r < r 0
E 0 ( x , У ) = E 0 ( r , ф ) = E 0 ( r ) = L (3)
[ 0, r > r 0. v '
В общем случае, когда входное поле представимо в радиально-вихревом виде:
E 0 ( r , ф ) = E 0 ( r ) exp( im ф ), (4)
выражение (2) можно упростить:
ст 0
E ( p , 0 , z ) = - i m + 1 k exp( im O ) j exp ( ikz 1 - ст 2 ) x
f r 0 1
x I j E 0( r ) J m ( k ст r ) rdr I J m ( k стp ) ст d ст
E 0 ( r , ф ) = exp ( - ik a 0 r + гт ф ) , (7) где а 0 - параметр конической волны, определяющий угол конуса и степень непараксиальности, m – порядок фазовой вихревой сингулярности.
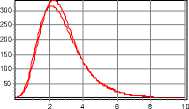
В табл. 1 приведены результаты численного моделирования с помощью выражения (5) дифракции волны (7) на отверстии радиусом 10 X при а 0 =0.5 и а 0 =0.9 для осесимметричного (m=0) и вихревого (m=1) случаев. Размер апертуры выбирался из соображений исследовать область, где еще работает скалярная модель, но уже существенно влияние поляризации.
Параметры расчета: r 0 = 10 X , шаг дискретизации Д r = 0, 01 X , ст 0 = 3 , шаг дискретизации Д ст = 0,01 . Картины интенсивности в поперечных плоскостях показаны в области радиусом p = 2 X .
По результатам моделирования, приведенным в табл. 1 видно, что при увеличении параметра конической волны а 0 для осесимметричного случая (m=0) происходит уменьшение размера центрального светового пятна. При а 0 =0.9 скалярная теория предсказывает преодоление дифракционного предела по полуспаду интенсивности (FWHM=0,39l), равный для линзы 0,51l.
При наличии вихревой составляющей на оптической оси будет нулевое значение интенсивности.
Однако в ближней зоне дифракции нельзя пренебрегать векторным характером электромагнитного поля, поэтому рассмотрим далее влияние поляризации на картину дифракции.
3. НЕПАРАКСИАЛЬНАЯ ВЕКТОРНАЯ МОДЕЛЬ
где r 0 - радиус ограничивающей апертуры, ст 0 -радиус учитываемых пространственных частот, m – порядок фазовой вихревой сингулярности.
При численном интегрировании дискретизация входного поля д r определяет (по теореме Найквиста) максимальное значение ст 0 :
ст 0
2 Д r ’
3.1. Алгоритм реализации векторного варианта интегральной теоремы Рэлея-Зоммерфельда
Интегральная теорема Рэлея-Зоммерфельда первого типа в векторной форме записывается следующим образом [2, 24, 25]:
jj E 0 x ( x , У )
S
E x ( u , v, z ) = -—
2n
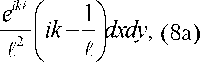
Распространяющимся волнам соответствуют пространственные частоты, расположенные в круге радиусом ст 0 < 1 , чтобы учесть также и затухающие волны, вносящие свой вклад на расстояниях меньше длины волны, необходимо увеличивать до значения, приведенного в выражении (6).
z e ik i f 1 1
E y (u , v , z )=-;- jj E 0 y ( x , yVp I ik -7 dxdy,’ (8б)
2П l V l у
S 0
2. ДИФРАКЦИЯ РАДИАЛЬНО-ВИХРЕВОГО ПОЛЯ В РАМКАХ НЕПАРАКСИАЛЬНОЙ СКАЛЯРНОЙ МОДЕЛИ
Ez (u,v, z) = -^ jj [ E0 x (x, y)(u - x) + E0 y (x, y)(v - y)] x n S0
eii / x— ik — \dddy
Рассмотрим дифракцию на круглом микроотверстии конической волны с вихревой составляющей [35]:
где E 0 x ( x , y ) , E 0 y ( x , y ) - тангенциальные компоненты входного электрического поля.
Алгоритм быстрого вычисления выражения
(1) был описан в работе [21]. Его можно приме-
Таблица 1. Дифракция конической вихревой волны в рамках непараксиальной скалярной модели.
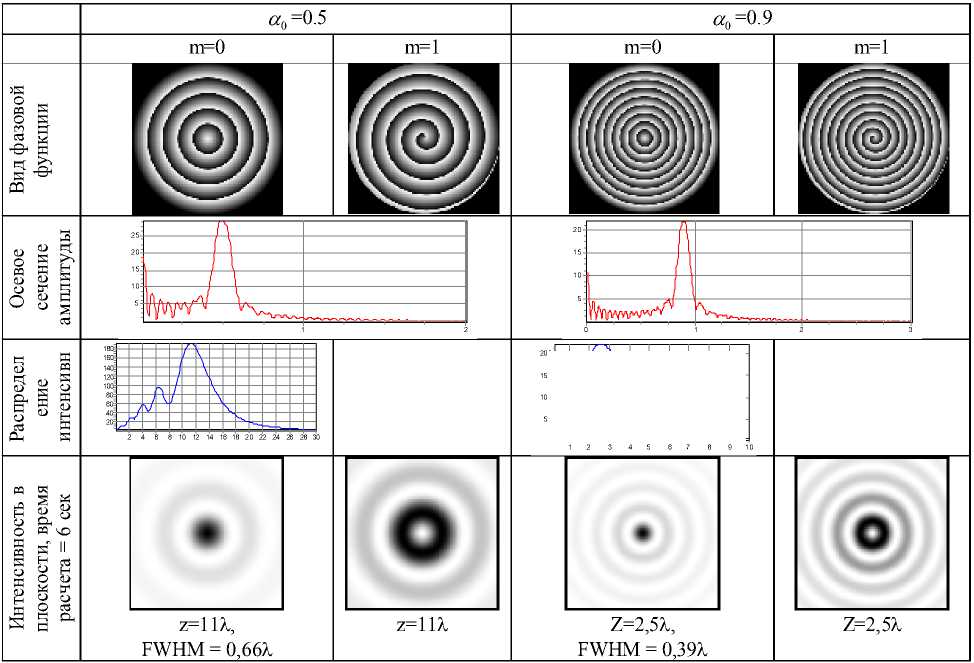
нить для вычисления выражений (8а) и (8б), однако для вычисления выражения (8в) требуется модификация, которая и рассмотрена в данном разделе.
В дальнейшем изложении учтём, что входная амплитуда задана не аналитическим выражением, а дискретным набором точек, и сделаем замену переменных p = u - x ; q = v - y . Так как в пределах каждой ячейки разбиения входная амплитуда является постоянной, то вычисления проводятся по дискретным формулам:
ikZ pm + 1 qM 1
E x ( X , У,z) = “' ^ 0 x [ mn ] J J eXP
2 n m P m q n
F ik^P 2 + q 2 + z2 "h ( P , q)df>dq
Ey ( x , y,z) =- k - Z E y [ mn ] J J exp F zk V p 2 + q 2 + z2hp,q)dpdq
2 n mn P m q .
ik P m + ' q n + 1
E z ( x,y,z) =— Z E x [ mn ] J J exp
2 n m,n P m q .
ik-j p 2 + q 2 + z2 Ph ( P, qyPdq -
ik Pm^qm 1 (9)
-t Z U o y [ m ” 1 J J exp l iksjp2 + q + z qh ( p, q)dpdq
2n m"P hP, q) = 2 2 2 + ,v 2 22x3/2
p2 + q 2 + z 2 k(p 2 + q + z )
где m, n – номера дискретного набора точек, в которых задано входное поле.
Если размер ячейки достаточно мал, в частности A < 0,2z (подробнее условия обсужда- ются в [21]), то можно считать функции h(p, q), ph (p, q), qh (p, q) в пределах ячейки постоянными. В этом случае упомянутые функции заменяются своими значениями в центре ячейки и выносятся за знак интеграла. При этом формулы (9) примут следующий вид:
ikz pm + 1 q n +l |- _________________
Ex(x,y,z)=-7ZEx[m,n]'h'P-,qn) 11 exp kp2+q2+z2 2П m. n Pm qn ikz Pm+l qn+1 |- _________________
E y ( x , y , z ) =-r Z E 0 y [ mn ] - h ( p m , q n ) J I exp l ik/p 2+ q 2 + z2 2n m- n P m q .
E z ( x, У , z ) =- -- Z F E 0x [ m. n ] - p m + U 0y [ m. n ] - q . ) h ( P m , q n ) n m,.
P m + 1 q n + 1
mmH qn+l .- ____________________-, j j explik/p2 + q2 + z2 tpcq где (~m, ~.) - центр ячейки.
Отсюда следует, что вычисления ничем не отличаются от скалярного варианта [21].
Если же вынесение за знак интеграла невозможно, то при вычислении продольной компоненты E z ( x , y , z ) необходимо вычислить два интеграла, которых не было в скалярном варианте.
Обобщение алгоритма на векторный случай
Также как и в скалярном варианте делается переход к полярным координатам, хотя подын- тегральная функция не является радиально симметричной. Тем не менее, по угловой переменной интеграл берётся аналитически, поэтому в результате придём к одномерному интегралу.
Нам необходимо вычислить интегралы следующего вида:
p 2 q 2 p 2 q 2
J J f (p2 + q2)pdpdq, J J f (p2 + q2)qdpdq pi q pi q p1 = um - x p2 = um +1 - x, q = vn - У q 2 = vn +1 - У, в котором область интегрирования – прямоугольник со сторонами, параллельными осям координат. В дальнейшем будем считать, что прямоугольник располагается в I четверти, так как к нему сводятся благодаря свойствам чётности и нечётности подынтегральной функции остальные возможности расположения прямоугольника. После замены переменных получатся интегралы JJ f (r)r2 cos фdrdф и JJ f (r) r2 sin ф drd ф, в кото-DD рых область D – некоторый криволинейный четырёхугольник. Интеграл по переменной ϕ берётся аналитически, но, так как стороны четырёхугольника описываются разными уравнениями, исходный интеграл превращается в сумму интегралов по переменной r. Пределы интегрирования зависят от того, как расположен исходный прямоугольник. Есть четыре варианта:
-
1) прямоугольник не соприкасается с осями координат;
-
2) прямоугольник соприкасается с осью Oq ;
-
3) прямоугольник соприкасается с осью Op ;
-
4) прямоугольник соприкасается с обеими осями.
В отличие от скалярного случая [21] варианты 1 и 4 не разделяются на два подварианта. (Более точно, ход вычислений немного различается, но конечный результат получается одинаковым.) Не будем описывать все варианты, рассмотрим только вариант 1 для интеграла JJ f (r)r2 cos фdrdф в случае, когда правая ниж-D няя вершина ближе левой верхней к началу координат. При вычислениях используются формулы sin(arcsinx) = x, sin(arccos x) = V1 - x2 , cos(arccos x) = x, cos(arcsin x) = V1 - x2 .
При замене переменных p = r cos ф ; q = r sin ф прямоугольник ABCD преобразуется в криволинейный четырёхугольник A’B’C’D’ (см. рис.1). Преобразование границ описывается соотношениями:
AB : p = p 2 ^ A ' B ': r cos ф = p 2 BC : q = q 2 ^ B ' C': r sin ф = q 2 CD : p = p1 ^ C' D': r cos ф = p1 DA : q = q1 ^ D ' A ': r sin ф = q1
Рис. 1 является схематичным: выпуклость или вогнутость границ не анализировалась.
Преобразование интеграла выражается формулами:
p 2 q 2
J J f(p2 + q2)pdpdq = p1 q 1
= JJ f ( r ) r 2 cos ф drd ф = JJ (-) + JJ (-) + JJ (-)
Q Q 1 Q 2 Q 3
r B arcsin( q 2 / r )
JJ f ( r ) r 2 cos ф drd ф = J f ( r ) r 2 dr J cos ф d ф =
П 1
arccos( p 2 / r )
r B 2
= j f (r)r2(q2 - 1-p2-)dr r r rC
F c arccos( p 1 / r )
JJ f ( r ) r 2 cos ф drd ф = J f ( r ) r 2 dr J cos ф d ф =
Q r A arccos( p 2 / r )
rc I Й2"
= J f (r)r2(J1 - p^ -r rA
J 1 - p 2- ) dr V r
r A arccos( p 1 / r )
JJ f ( r ) r 2 cos ф drd ф = J f ( r ) r 2 dr
Q 3 rD arcsin( q 1 / r )
J cos ф d ф =
r A 2
= J f (r) r 2(J1 - p^ - q1) dr r r rD
Если теперь раскрыть скобки и объединить интегралы с одинаковой подынтегральной функцией, то получим, что
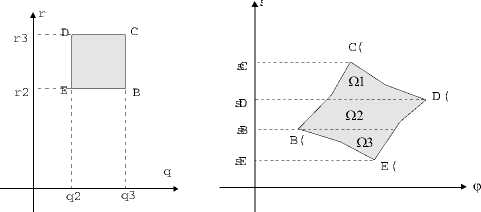
Рис. 1. Пояснения к преобразованию границ области при замене переменных
JJ f ( r ) r 2 cos
Q
rC ф drd ф = J f (r) r2
rD
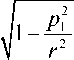
Аналогичное преобразование интеграла (13) имеет вид:
rB
" J f ( r ) r 2^1
2 rBrA
--Y dr + q 2 J f ( r ) rdr - q1 J f ( r ) rdr .
r rCrD
r 2 2 r 2
J f ( r ) r 2 Ji—2" dr = J f (r)r\r 2 - a 2 dr
Аналогично можно доказать, что и в остальных вариантах расположения исходной прямоугольной области интегрирования интеграл преобразуется в линейную комбинацию интегралов вида:
■ J f ( r ) rdr = ^—5 r 1
■ i
f e i'
V t i
eV 1
' 2 7
,(16)
которое применимо при выполнении неравенства
r 2
r 1
r 2
J f ( r ) r 2 dr , r 1
a 2( r 2 - r 1 )2 п 2
( r s 2 - a 2)2 < 384 . (17)
1 - —dr . r 2
r 1
В формулах (11)-(13) r 1, r 2 – полярные радиусы некоторых вершин прямоугольника, a – одно из чисел p 1, p 2, q 1, q 2 , причём гарантировано, что подкоренное выражение неотрицательно. Интеграл вида (5) появляется при соприкосновении области интегрирования с осью координат, что при переходе к полярной системе даёт постоянный предел интегрирования (0 или п /2 ).
Подставим в формулы (11)-(13) функцию
f ( r ) = exp
ik4r^ + Z
f 1 i 1
V r 2 + z2 + k ( r 2 + z T ,
3.2. Аппроксимация интеграла Рэлея-Зоммерфельда для микроапертур
Хотя алгоритм, рассмотренный в предыдущем разделе, значительно уменьшает время расчета выражений (8) по сравнению с прямыми квадратурными формулами, затраты эти все же существенные (см. далее результаты моделирования).
Рассмотрим аппроксимацию интегралов (8) при условии, что расстояние до точки наблюдения достаточно велико по сравнению с размерами апертуры [7, 36]. Такая аппроксимация является более точной, чем хорошо известная параксиальная аппроксимация, рассматривающая лишь область возле оптической оси.
При подстановке в выражениях (8) в подынтегральные экспоненты
Интеграл (11) вычисляется в явном виде: он ра-
l _ R + r 2 - 2( ux + vy ) 2 R ,
вен
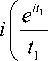
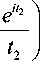
где '1 = k^r2 + z2 ,
где R = V u 2 + v 2 + z 2 , r = -^ x 2 + У2 , а в осталь
ные места l ^ R , а также пренебрегая слагаемым
' 2 = k^jr ^ + z 2 (см. описание скалярного варианта в [21]). Интегралы (12) и (13) вычисляются или по квадратурным формулам, или с применением асимптотических формул, аналогичных скалярному варианту.
Для интеграла (12) преобразование имеет вид:
с 3 , получаем: R
E x ( Р , 6 , z ) = "
iz exp ( ikR ) IR2
r 0
r
J f ( r ) r 2 dr * r s
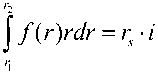
f e it
V t i
e i2 1
T ,(14)
' 2 7
где r s = ( r 1 + r 2)/2 . Оно применимо, если вы-
полняется неравенство
r - r п2—--1 <---
2 rs 384 .
exp ik r
J0 V 2 R
^ j E ox ( r ,*xp r- ikr ^ cos fcf » . 0 L 2V
iz exp ikR
E y ( P , 9 , z ) = '( )
I R
r 0
(19а)
4 ф> rdr ,
r
.2 7
f -1 r exp ik
0 V 2 R
^ \ E o , ( r , p )ex, Г- ik W- f ) o
X
(19б) rdr ,
E z ( P , 9 , z )
i exp ( ikR ) A R 2
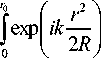
2 n
J[E0 x (r, 0)( Pcos9 - r cos ^)+ E0 y (r, ^ ( Psin9 - r sin ^)]X exp ^'"Т *' ] Urd
(19в)
Если тангенциальные компоненты входного поля представимы в радиально-вихревом виде (4) (например, для линейной и эллиптической поляризаций) и учитывая, что
2 n J 0
^2 c exp( im ф ) exp [ i a cos( ф 0 ) ] d ф = ]
Под интенсивностью здесь и далее понимается сумма модулей в кв 2 адрате 2 всех к 2 омпон 2 ент электрического поля: I E l2 =1 E x l2 +1 E y l +1 E z f •
-
3.3. Быстрый алгоритм расчета распространения радиально-вихревых полей на основе разложения по плоским волнам
Полученные в предыдущем разделе формулы (21) просты в реализации и обеспечивают высокую скорость вычислений, но они являются приближенными в соответствии с (18), и при уменьшении расстояния от входной плоскости, т.е. в ближней зоне дифракции, будут давать неверный результат.
Для получения более точных выражений рассмотрим векторный вариант оператора распространения, использующего разложение по плоским волнам [26, 27]:
= 2 nE c q i m exP(im q 0Jmq ( « ) . (20)
q
Выражения (19) можно упростить:
f E x ( X , y , z ) ]
E ( x , y , z )
z im + 1 zk exp ( ikR ) z z
E x ( P , 9 , z ) =------ exp( im9 ) X
R
E y ( X , y , z )
V E z ( x , y , z ) J
= JJ M ( ^ , П )
S s
f F x ( ^ , П ) "x v F y ( ^ , П ) У"
x exp Г ikz^ 1 - ( ^ 2 + n 2) ] exp [ ik ( ^ x + n y ) ] d ^ d n
, (22)
r 0
X
r
J exp ikrA E 0 X ( r ) J, 0 V 2 R J
. f kr p ] (2 1a)
m I T Г ,
E y ( P* , z )
im + 1 zk exp ( ikR )
R 2
exp( im 9 ) x
r 0
X
r
J exp ik^ E 0 y ( r ) J 0 V 2 R J
. ( kr p ] (216)
m I T Г,
где fFx (^, П) ] 1 rrf E0 x (x, y) ] г ,
I F y ( ^ , n ) J = A 2 '■ E 0 y ( x , y ) J exp [" ik ( ^ x + n y ) ] d x d y (23) y S o x y
-
- спектры тангенциальных компонент входного электрического поля определенного в области S o , и матрица преобразования:
г k exp ( ikR) z
E z ( P,9 . z ) =---- ^—" exp im *:
R
M E ( ^Л ) =
n
r- r 2
P exp к [E x ( r )C0S 9 + E y ( r )™ 9 ] J m
. 0 V 2 R J
<
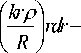
Ti- c i ^ + n^ V 1 - ( ^ 2 + n 2)
i r »i f k P] - * f kr P )! 2
^Jexp V ik2R J E 0X ( r) \ e J m + 1 V R J" e J m - 1 V R J\ rdr - (21в)
-
1 f r 2 V f J * r f krPV " i * т f k" P )1 2
" 2 J exp | ik 2 R J E l y ( r ) | e J m + 1 V R J+ e J m1 V R J r dr ‘
В полярных координатах выражения (22)(24) принимают следующий вид:
Из выражений (21) видно, что при учете векторного характера электромагнитного поля для |m | = 1 возможно ненулевое значение интенсивности на оптической оси, причем за счет z-компоненты. Данный факт также отмечался при рассмотрении высокоапертурных фокусирующих систем [31].
1 ° ] 2 n
E ( p , 0 , z ) = -y J J P ( o , Ф ) exp [ ik op cos( 0 - ф ) ] Л
° 1 0
x exp Г ikz V1 -o 2 ]o d o d ф
P ( o , ф ) =
o cos ф
4 1 - o 2
o sin ф
4 1 - o 2
X
, (25)
Г F x ) )
V F y ( o , ф ) J . (26)
( F x ( о ; ф ) ) r iV E x ( г , ф )) r
, х = и ( А exp [ k no°4 ф) ] ddN, (27)
V F '0'» 00 ( E у l r n> ,( )
Учитывая радиально-вихревой вид компонент входного поля:
r 0
= im exp( im ф ) j
^ F x ( ^ ф ) ' V F y (°’ ф ) >
= 2 n im exp( im ф )
( P x ( o ) )
V P 4
( E ( r ) ^
0 x J m ( kr o )rdr =
V E 0 у (r) )
, (28)
выражения (16)-(18) также можно упростить:
E ( P,O ; Z )
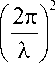
i2 m exp(imO) x o2
x
j exp ikz^ 1 —o 2 Q m ( k op , O ) □ d □
□i где
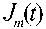
Q t O ) =
J m (t)
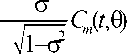
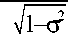
S X t O)
\ P x "
V P (4(30)
где C , ( t . в ) = 2 [ У - J m + 1 ( t ) - e -” J m . , ( t ) ] , S m ( t . в ) = 2 [ eJ + , ( t ) + e -4 - 1 ( t ) ] , t = k ep .
В дальней зоне дифракции можно получить аналитический вид выражений (29) методом стационарной фазы [37], но в ближней зоне их использовать некорректно.
В табл. 2 приведены сравнительные результаты численного моделирования с помощью векторных дифракционных интегралов Релея-Зом-мерфельда (8), аппроксимирующих формул (21) и разложения по плоским волнам с учетом радиально-вихревой симметрии (28)-(30) дифракции линейно-поляризованной волны (7) на отверстии радиусом 10Л при a0 =0.5 для осесимметричного (m=0) и вихревого (m=1) случаев. Параметры расчета для выражений (8): шаг дискретизации на входе и выходе Ах = Ау = 0; 12 ; для выражений (12): шаг дискретизации на входе и выходе Аr = 0;012 ; для выражений (19)-(21) шаг дискретизации в объектной плоскости Аr = 0;012 , шаг дискретизации в спектральной области Ае = 0; 01, e0 = 3. Картины интенсивно- сти в поперечных плоскостях показаны в области радиусом p = 22 .
Время расчета приведено для персонального компьютера Pentium®4, CPU 2,40GHz.
Как видно из табл. 2, применение аппроксимационных формул (21) в ближней зоне дифракции некорректно, в то время как выражения (28)(30) позволяют получить с меньшими временными затратами результат, практически совпадающий с вычислениями по формулам Ре-лея-Зоммерфельда.
Также видно, что учет поляризационных эффектов сказывается на картине дифракции: за счет вклада продольной компоненты теряется радиальная симметрия. При этом в случае отсутствия фазовой вихревой сингулярности (m=0) центральное световое пятно вытягивается (уширяется) вдоль оси поляризации, а при наличии фазовой вихревой сингулярности первого порядка (|m|=1) появляется ненулевое значение интенсивности на оптической оси. При увеличении параметра конической волны а 0 вклад продольной компоненты будет расти, и описанные явления будут проявляться с большей очевидностью.
В табл. 3 приведены сравнительные результаты численного моделирования с помощью векторных дифракционных интегралов Релея-Зом-мерфельда (8) и разложения по плоским волнам с учетом радиально-вихревой симметрии (28)(30) дифракции линейно-поляризованной волны (7) на отверстии радиусом 10 2 при а 0 =0,9 для осесимметричного (m=0) и вихревого (m=1) случаев. Параметры расчета такие же, как в предыдущем эксперименте.
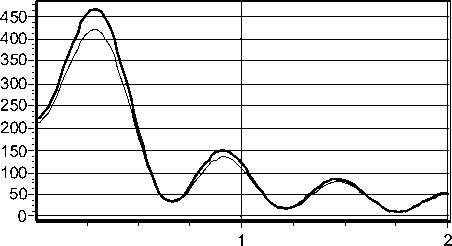
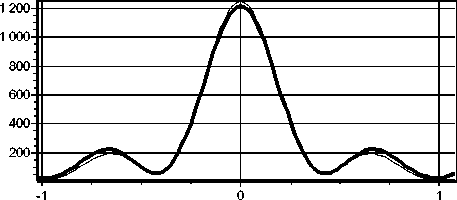
На рис. 2 показаны сравнительные графики радиальных сечений распределений суммарной интенсивности в поперечных плоскостях, соответствующих максимальному значению интенсивности на оптической оси. Среднеквадратичное отклонение полученных результатов при m=0 составило 7,4%, а при m=1 – 3,5%.
Из табл. 3 видно, что при увеличении значения параметра конической волны а 0 в ближней зоне дифракции происходит усиление продольной компоненты, что приводит к существенному изменению картины суммарной интенсивности. В этом случае при линейной поляризации наличие вихревой составляющей первого порядка позволяет существенно сузить размер центрального светового пятна вдоль направления оси поляризации. Данный эффект был также рассмотрен в [31].
Аналогичные результаты получаются при реализации формул (22)-(24) с использованием алгоритма БПФ. В этом случае при меньших временных затратах (несколько секунд) требуются значительные ресурсы оперативной памяти (при рассмотренных параметрах понадоби-
Таблица 2. Дифракция линейно-поляризованной конической вихревой волны при α 0 =0.5 в рамках непараксиальной векторной модели (интенсивность x-компоненты показана светло-серым цветом, z-компонента – тонкой линией, суммарная интенсивность – толстой)
лось более 400 Мб). Этот недостаток компенсируется универсальностью, т.е. возможностью применения данного алгоритма для задач, не обладающих радиальной симметрией.
В табл. 4 приведены сравнительные результаты численного моделирования с помощью векторных дифракционных интегралов Релея-Зом-мерфельда (8) и разложения по плоским волнам
(22)-(24) с использованием БПФ дифракции радиально-поляризованной волны (7) на отверстии радиусом 10 λ при α 0 =0,9 для осесимметричного (m=0) и вихревого (m=1) случаев.
На рис. 3 показаны сравнительные графики радиальных сечений распределений суммарной интенсивности в поперечных плоскостях, соответствующих максимальному значению интен-
Таблица 3. Дифракция линейно-поляризованной конической вихревой волны при α 0 =0,9 в рамках непараксиальной векторной модели, рассчитанная по выражениям (8) (тонкая линия) и (28)-(30) (толстая линия)
'Г,
Интенсивность на оптической оси
Распределение в плоскости z0,
ρ
∈
[0, 2
λ
]
Ex
,
arg
Ex
FWHM = 0,39λ E FWHM ( | ) = 0,39λ FWHM (-) = 0,31λ FWHM (-) = 0,37λ (а)
Рис. 2.
Сравнительные графики радиальных сечений распределений суммарной интенсивности в поперечных плоскостях на расстоянии z0=2,6
λ
для m=0 (а) и расстоянии z0=2,25
λ
для m=1 (б):
тонкая линия соответствует расчетам с помощью выражения (8), а толстая – с помощью (28)-(30) (б)
Таблица 4.
Дифракция радиально-поляризованной конической вихревой волны при
α
0
=0,9 в рамках непараксиальной векторной модели, рассчитанная по выражениям (8) и с использованием БПФ в формулах (22)-(24)
Распределение в плоскости z0,
ρ
∈
[0, 2
λ
]
E
x
,
arg
E
x
,
arg
E
y
,
y
E
z
,
arg
E
z
E FWHM (-)= 0,32λ
------ l
’^■e^'
j
FWHM = 0,39λ FWHM = 0,41λ сивности на оптической оси. Среднеквадратичное отклонение полученных результатов при m=0 составило 4,9%, а при m=1 – 7,5%. Заметим, что в отличие от скалярного случая, рассмотренного в [10, 17, 19, 20], в векторном варианте разложения по плоским волнам (а)
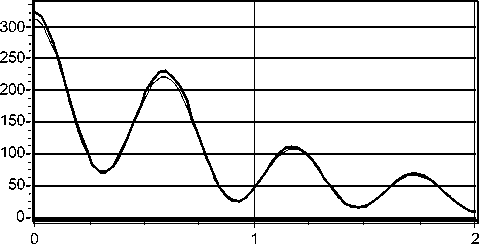
Рис. 3.
Сравнительные графики радиальных сечений распределений суммарной интенсивности в поперечных плоскостях на расстоянии z0=2,15l для m=0 (а) и расстоянии z0=2,6l для m=1 (б): тонкая линия соответствует расчетам с помощью выражения (8); толстая – с использованием БПФ в формулах (22)-(24).
имеется особенность при вычислении продольной компоненты. Как следует из поляризационной матрицы (24) и соответствующей матрицы (26) при достижении спектральных частот радиуса, близкого к единице ^
2
+ п
2
= с
2
= 1, что соответствует для конической волны а
0
= 1 предельному наклону лучей, возникает особенность. Данная особенность не соответствует входному распределению, т.к. приводит к резкому росту продольной компоненты при z=0, поэтому в разработанных алгоритмах в спектральной плоскости игнорируется узкая кольцевая область, средний радиус которой
с
2
=
1
, а ширина Ас = 0,01.
ЗАКЛЮЧЕНИЕ В данной работе рассмотрены:
- обобщение быстрого алгоритма вычисления интегрального преобразования Релея-Зоммер-фельда первого типа в векторной форме;
- непараксиальная аппроксимация дифракционных интегралов Релея-Зоммерфельда при радиально-вихревой симметрии;
- быстрый алгоритм моделирования непараксиального распространения на основе разложения по плоским волнам при радиально-вихревой симметрии;
- особенности реализации векторного оператора распространения на основе разложения по плоским волнам.
Проведено сравнение работы рассмотренных алгоритмов на примере моделирования дифракции вихревой конической волны на микроапертуре в ближней зоне. Показана эффективность в ближней зоне дифракции предложенного алгоритма непараксиального векторного распространения на основе разложения по плоским волнам с учетом радиально-вихревой симметрии по точности и экономии вычислительных ресурсов: при погрешности 4-8% обеспечивается сокращение времени вычислений в 7 раз. Если в задаче не имеется радиальной симметрии, целесообразно использовать метод разложения по плоским волнам, реализованный через БПФ. Векторный вариант данного метода име- ет особенность, возникающую в продольной компоненте при стремлении числовой апертуры оптической системы к предельному значению. В этом случае можно игнорировать в спектральной плоскости узкую кольцевую область или применять быстрый алгоритм, разработанный для вычисления дифракционных интегралов Рэлея-Зоммерфельда в векторной форме. Работа выполнена при поддержке российско-американской программы “Фундаментальные исследования и высшее образование” (грант CRDF PG08-014-1), грантов РФФИ 10-07-00109-а, 10-07-00438-а и гранта Президента РФ поддержки ведущих научных школ НШ-7414.2010.





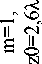







Список литературы Алгоритмы быстрого расчета дифракции радиально вихревых лазерных полей на микроапертуре
- Martinez-Herrero R., Mejias P.M., Bosch S., Carnicer A. Vectorial structure of nonparaxial electromagnetic beams, J. Opt. Soc. Am. A. 2001. Vol. 18. Pp. 1678-1680.
- Ciattoni A., Crosignani B., and Porto P.D. Vectorial analytical description of propagation of a highly nonparaxial beam//Opt. Commun. 2002. Vol. 202. Pp. 17-20.
- Shekhar Guha, Glen D. Gillen. Description of light propagation through a circular aperture using nonparaxial vector diffraction theory//OPTICS EXPRESS. 2005. Vol. 13. No. 5. Pp. 1424-1447.
- Hanming Guo, Jiabi Chen, Songlin Zhuang. Vector plane wave spectrum of an arbitrary polarized electromagnetic wave//OPTICS EXPRESS. 2006. Vol. 14, No. 6.
- Dongmei Deng and Qi Guo. Analytical vectorial structure of radially polarized light beams//OPTICS LETTERS. 2007. Vol. 32. No.18. Pp. 2711-2713.
- Anokhov S.P. Plane wave diffraction by a perfectly transparent half-plane//J. Opt. Soc. Am. A. 2007. Vol.24. No.9, Pp. 2493-2498.
- Ковалев А.А., Котляр В.В. Непараксиальная векторная дифракция гауссового пучка на спиральной фазовой пластинке//Компьютерная оптика. 2007. T. 31. №4. Pp.19-22.
- Guohua Wu, Qihong Lou, Jun Zhou. Analytical vectorial structure of hollow Gaussian beams in the far field//OPTICS EXPRESS. 2008. Vol. 16. No. 9. Pp. 6417-6424.
- Guoquan Zhou. The analytical vectorial structure of a nonparaxial Gaussian beam close to the source, OPTICS EXPRESS. 2008. Vol. 16. No. 6. Pp. 3504-3514.
- Nuri Delen and Brian Hooker. Verification and comparison of a fast Fourier transform)based full diffraction method for tilted and offset planes, APPLIED OPTICS//2001. Vol. 40. No. 21. Pp. 3525-3531.
- Cooper I.J., Sheppard C.J.R., Sharma M. Numerical integration of diffraction integrals for a circular aperture//Optik. 2002. Vol. 113. No.7. Pp. 293-298.
- Kailiang Duan, Baida Lu. A comparison of the vectorial nonparaxial approach with Fresnel and Fraunhofer approximations//Optik. Vol. 115. No.5. Pp. 218-222.
- Cooper I.J., Sheppard C.J.R., Roy M. The numerical integration of fundamental difraction integrals for converging polarized spherical waves using a two-dimensional form of Simpson's 1/3 Rule//Journal of Modern Optics. 2005. Vol. 52. No. 8. Pp. 1123-1134.
- Jan A. C. Veerman, Jurgen J. Rusch and H. Paul Urbach. Calculation of the Rayleigh-Sommerfeld diffraction integral by exact integration of the fast oscillating factor//J. Opt. Soc. Am. A. 2005. Vol. 22. No. 4. Pp. 636-646.
- Zhiguo Zhao, Kailiang Duan, Baida Lu. Focusing and diffraction by an optical lens and a small circular aperture//Optik. 2006. Vol. 117. Pp. 253-258.
- Xueen Wang, Zhaozhong Fan and Tiantong Tang. Numerical calculation of a converging vector electromagnetic wave diffracted by an aperture by using Borgnis potentials. I. General theory//J. Opt. Soc. Am. A. 2006. Vol.23. No.4. Pp. 872-877.
- Fabin Shen and Anbo Wang. Fast-Fourier-transform based numerical integration method for the Rayleigh-Sommerfeld diffraction formula, APPLIED OPTICS//Vol. 45. No. 6. Pp. 1102-1110.
- Sharp focus area of radially-polarized Gaussian beam by propagation through an axicon/Kotlyar V.V., Kovalev A.A., Stafeev S.S.//Prog. In Electr. Res. C. 2008. Vol. 5. Pp.35-43.
- Victor Nascov and Petre Cãtãlin Logofãtu. Fast computation algorithm for the Rayleigh-Sommerfeld diffraction formula using a type of scaled convolution//APPLIED OPTICS. 2009. Vol. 48. No. 22. Pp. 4310-4319.
- Kyoji Matsushima, Tomoyoshi Shimobaba. Band-Limited Angular Spectrum Method for Numerical Simulation of Free-Space Propagation in Far and Near Fields//OPTICS EXPRESS. 2009. Vol. 17. No. 22. Pp.19662-19673.
- Устинов А.В. Быстрый способ вычисления интеграла Рэлея)Зоммерфельда первого типа,//Компьютерная оптика. 2009. Т. 33, № 4. С. 412-419.
- Totzeck M. Validity of the scalar Kirchhoff and Rayleigh-Sommerfeld diffraction theories in the near field of small phase objects//J. Opt. Soc. Am. A. 1991. V. 8. No. 1. Pp. 27-32.
- Tsoy V.I., Melnikov L.A. The use of Kirchhof approach for the calculation of the near feld amplitudes of electromagnetic feld//Optics Communications. 2005. V. 256. Pp. 1-9.
- Luneburg R.K. Mathematical Theory of Optics, University of California Press, Berkeley, California, 1966.
- Lü B.D., Duan K.L. Nonparaxial propagation of vectorial Gaussian beams diffracted at a circular aperture//Opt. Lett. 2003. No. 28. Pp. 2440-2442.
- Carter W.H. Electromagnetic Field of a Gaussian Beam with an Elliptical Cross Section//J. Opt. Soc. Am. A. Vol. 62. No.10. Pp. 1195-1201.
- Agrawal G.P., Pattanayak D.N. Gaussian beam propagation beyond the paraxial approximation//J. Opt. Soc. Am. A. vol.69, No.4, 575-578 (1979).
- Ковалев А.А., Котляр В.В. Дифракция плоской волны на ограниченной спиральной фазовой пластинке: параксиальная векторная теория//Компьютерная оптика. 2007. T. 31. №2, Pp. 4-8.
- Khonina S.N., Kotlyar V.V., Soifer V.A., Shinkaryev M.V., Uspleniev G.V./Trochoson//Optics Communications 1992. No. 91 (3)4), Pp.158-162.
- Павельев В.С., Хонина С.Н. Быстрый итерационный расчет фазовых формирователей мод Гаусса-Лагерра//Компьютерная оптика. 1997. Вып. 17. С. 15-20.
- Хонина С.Н., Волотовский С.Г. Исследование применения аксиконов в высокоапертурной фокусирующей системе//Компьютерная оптика. 2010. Т. 34. №1. С. 35-51.
- Khonina S.N., Kotlyar V.V., Soifer V.A. Fast Hankel transform for focusator synthesis//Optik. 1991. No. 88 (4). Pp. 182-184.
- Goodman J.W. Introduction to Fourier Optics (McGraw-Hill, 1968), Chap. 3.
- Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука. Главная редакция физико-математической литературы, 1979. 384 с.
- Victor V. Kotlyar, Alexey A. Kovalev, Svetlana N. Khonina, Roman V. Skidanov, Victor A. Soifer, Henna Elfstrom, Noora Tossavainen, and Jari Turunen. Diffraction of conic and Gaussian beams by a spiral phase plate//APPLIED OPTICS. 2006. Vol. 45. No.12. Pp. 2656-2665.
- Yaoju Zhang, Ling Wang, Chongwei Zheng. Vector propagation of radially polarized Gaussian beams diffracted by an axicon//J. Opt. Soc. Am. A. 2005. Vol. 22, No. 11. 2542-2542.
- Guoquan Zhou. Analytical vectorial structure of controllable dark-hollow beams in the far field//J. Opt. Soc. Am. A. 2009. Vol. 26, No. 7. 1654-1660.


