Алгоритмы двумерного гиперкомплексного дискретного преобразования Фурье

Многомерное гиперкомплексное дискретное преобразования Фурье (ГДПФ) [1] вещественного сигнала:

N -1

F ( m i ,...,m d ) = Е f ( n n-, n d ) W <^m,n> ,

" 1.-. n d =0

d w=n wmknk, wN =1,                  (i)

k =1

привлекает все больше внимания специалистов в области обработки изображений и многомерных сигналов. Его приложениям посвящен целый ряд работ российских и зарубежных ученых (см., например, [3, 4, 5]).

Особенностью преобразования (1) является то, что корни w_k N -ой степени из единицы лежат в различных подалгебрах, изоморфных алгебре комплексных чисел C, некоторой 2 ^d -мерной коммутативной алгебры B d . Соответственно и значения спектра F ( т 1 ,..., m d ) лежат в алгебре B d . В двумерном случае ( d =2) преобразование (1) принимает вид:

N -1 N -1

F ( m_b m 2 ) = Е Е f ( ⁿ 1 , n 2 ) w m ¹ n ¹ w m ^{2 n 2} ,     ⁽²⁾

n =0 n 2 =0

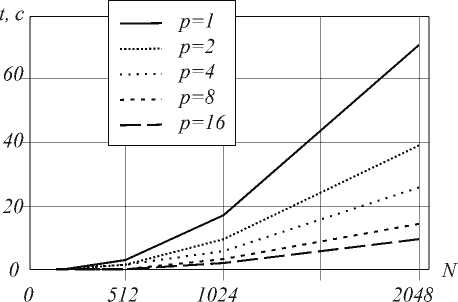
0

z=a+Ps₁+ys₂+3s1s₂.                        (3)

Заметим, что классическое многомерное дискретное преобразование Фурье является частным случаем преобразования (1) при s1 =...=sd = ieC . Это позволяет утверждать, что, кроме целого ряда специальных приложений, рассмотренных в [3], [4], [5], преобразование (1) позволяет эффективно решать весь круг задач цифровой обработки сигналов, для решения которых используется дискретное преобразование

Фурье (быстрое вычисление дискретной свертки, фильтрация, компрессия сигналов и т.д.).

Как отмечено в [1], принципиальным свойством, определяющим эффективность применения ГДПФ в прикладных задачах, является не конкретная структура гиперкомплексной алгебры B_d , а только существование в ней достаточного количества изоморфных копий комплексной алгебры. В работе [1] доказано, что минимальное количество вещественных операций, необходимых для сложения/умножения элементов B_d , достигается при:

в d = сесв...® с.                         (4)

'V'

2 d-1

Кроме того, в [1], [2] построена система автоморфизмов, разработан алгоритм быстрого умножения элементов алгебры Bd , синтезированы «последовательные» алгоритмы ГДПФ.

Параллельный алгоритм ГДПФ, основанный на структуре гиперкомплексной алгебры

Основная проблема при реализации многомерного преобразования - это увеличение объема вычислений с ростом размерности. Одним из наиболее естественных путей решения этой проблемы является параллельная реализация преобразования (1). Очевидно, что в представлении (4) заложена принципиальная возможность такой реализации. Кроме того, дополнительные возможности для повышения степени распараллеливания и эффективности алгоритма предоставляет внутренний параллелизм многомерной схемы Кули-Тьюки, аналог которой используется для формирования гиперкомплексного спектра.

Рассмотрим принципы формирования такого параллельного алгоритма на примере двумерного преобразования. Пусть произвольный элемент z четырехмерной алгебры В₂определен соотношением (3).

Введем замену переменных:

Uо —1 + S1S2 , U1 —1 S1S2 ,

U2 —S1 S2 , U3 —S1 +S2 .

Тогда гиперкомплексное число z запишется в виде:

• z =2 ((а+З) u 0 +(а-5) u₁ +(P-y) u₂+(P+y) u 3). (5)

Очевидно, что для произвольного z eB₂переход к представлению (5) потребует четырех вещественных сложений. Однако для вещественных (входной сигнал) и комплексных (корни w_k ) чисел этот переход не потребует выполнения нетривиальных арифметических операций.

Обратный переход к исходному представлению так же требует четырех вещественных сложений на отсчет гиперкомплексного спектра.

Правило умножения новых базисных элементов представлено в таблице 1.

Таблица 1. Правило умножения базисных элементов

Необходимо отметить, что в таком представлении произведения элементов u₀и u₂с элементами u₁и u₃равны нулю. Это означает, что вычисление произведения двух произвольных гиперкомплексных чисел состоит в таком представлении из двух совершенно независимых частей. Вместо произведения:

(xu0 + yu₁ + zu₂+ vu3 )(аu₀+ Pu₁ +yu₂+Зu3)

достаточно независимо вычислить два произведения:

(xu₀+ zu₂) (а u₀+y u₂ )=

• = 2 ((x а-zy) u₀+(x y + z а) u₂)

(yu₁ + vu3 )(pu₁ +Зu3 )=

=2((yP—vЗ)u₁ +(yЗ+vP)u3).

Таким образом, наиболее трудоемкая операция алгоритма – вычисление произведения гиперкомплексных чисел может быть распараллелена на две независимые ветви, не требующие обмена данными.

Структура последовательного быстрого алгоритма ГДПФ [1] такова, что при использовании представления (5) возможно полное разделение вычислений по тому же принципу. В результате, мы приходим к следующему параллельному алгоритму двумерного ГДПФ:

• -    переход от исходного представления (3) к представлению (5);

• -    распределение данных по двум процессорам;

• -    расчет преобразования (2) с использованием алгоритмов типа Кули-Тьюки [2];

• -    реконструкция гиперкомплексного спектра.

Загрузка процессоров проиллюстрирована на рис. 1.

К достоинствам такого метода распараллеливания двумерного гиперкомплексного ДПФ можно отнести:

• -    снижение сложности операций сложения гиперкомплексных чисел и умножения комплексного корня на гиперкомплексное число в 2 раза;

• -    снижение сложности умножения двух произвольных гиперкомплексных чисел более чем в 3 раза;

• -    сохранение возможности учета симметрий гиперкомплексного спектра вещественного сигнала [1, 2].

Номер процессора

I

II

Время

Передача данных

Работа процессора

Простой

Рис.1. Иллюстрация загрузки процессоров при распараллеливании за счет структуры алгебры

Однако для учета симметрий потребуется дополнительный обмен данными, что несколько снизит общую эффективность распараллеливания.

Распараллеливание за счет структуры декомпозиции

Описанный выше подход уже позволяет синтезировать параллельный алгоритм d-мерного ГДПФ с распараллеливанием на 2d-1 процессоров. Соответственно и ускорение алгоритма не превысит величины 2d^-1. При наличии большего числа процессоров целесообразно провести дополнительное распараллеливание за счет структуры многомерной декомпозиции Кули-Тьюки. Принцип распределения данных и вычислений показан ниже на примере двумерного преобразования.

Основное соотношение декомпозиции ГДПФ (2) «по основанию 2» [2] имеет вид:

F (ml, m2 )= £ F'ab (ml,m2 ) wam¹wm²,       (6)

• a, b=0

где

Fab ( ml, m 2 ) =

N

• ²                        mn mn

E f ( ²”1 ^{+ a ,2}n 2 ^{+ b} )( ^W2 )   ( w2 )    .

П1, n 2 =0

Ключевой операцией в таком алгоритме является реконструкция (6) полного спектра F (m1, m2) по известным (найденным) значениям частичных спектров Fab (m1, m2). Предположим, что каждый частичный спектр рассчитан на отдельном процессоре, причем время работы процессоров будет примерно одинаковым (так как одинаковы размеры массивов вычисляемых спектров и алгоритм их вычисления). Далее, на каждом процессоре выполняется умножение элементов частичного спектра на степени кор- ней w1, w2. Затем полученные значения пересылаются на один из процессоров, где окончательно формируется гиперкомплексный спектр.

Ясно, что таким способом процесс может быть распараллелен на любое число процессоров кратное четырем за счет нескольких шагов декомпозиции типа (6). Предполагаемое время вычисления гиперкомплексного спектра обратно пропорционально числу процессоров, так как основные вычислительные затраты приходятся на расчет набора ГДПФ уменьшенного размера. В случае размерности данных d>2 может быть применена аналогичная схема с распараллеливанием на каждом шаге на 2^d процессов.

Иллюстрация загрузки процессоров при реализации описанного подхода для двумерного случая приведена на рис. 2.

Номер процессора

I

II ■ ■ ■ ■ ^  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^ee ■ i ■■■■■■■■■■■■■■■■■■■■■■■i

III • ■ • ■ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^™e el ■■■■••■■•■■•■■•■■•■■•■■<

IV ■ ■ ■ ■ g=^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™ ^^^^^^™ ■■■■■■■■■■■■■■■■■■■■■■■i

Время

Передача данных

^^^^^^ Работа процессора

Простой

Рис. 2. Иллюстрация загрузки процессоров при распараллеливании за счет структуры декомпозиции

Достоинством такого подхода является уменьшенный объем пересылаемых данных за счет учета симметрий гиперкомплексного спектра вещественного сигнала (свойства гиперкомплексного спектра вещественного сигнала описаны, например, в [1, 2]).

Экспериментальное исследование

К настоящему времени реализован и исследован параллельный алгоритм двумерного гиперкомплексного дискретного преобразования Фурье на основе использования структуры алгебры, схемы декомпозиции, а также комбинированный алгоритм, использующий оба подхода одновременно.

В соответствии с этим ниже приведены результаты распараллеливания алгоритма преобразования для ситуаций, перечисленных в таблице 2 (p – количество процессоров).

Таблица 2. Исследованные случаи

Исследования проводились на кластере научноисследовательского вычислительного центра МГУ (НИВЦ МГУ), который состоит из 16 двухпроцес- сорных узлов с процессорами Pentium III, соединенных высокоскоростной сетью SCI.

На рис.3 приведено время Tp (в секундах) выполнения программы в зависимости от N, где N×N – размер двумерного ГДПФ.

В таблицах 3 и 4 приведены значения ускорения алгоритма U= T₁jT_p и эффективности E=T₁I pT_p , полученные по экспериментальным данным.

Рис.3. Время вычисления N×N – ГДПФ

Таблица 3. Ускорение алгоритма

Таблица 4. Эффективность алгоритма

Заключение

В статье рассмотрены принципы синтеза параллельных алгоритмов двумерного гиперкомплексного дискретного преобразования Фурье. Предложены два способа распараллеливания преобразования. Наилучшая эффективность достигнута при использовании алгоритма, основанного на структурных свойствах алгебры (около 90%). Эффективность использования для распараллеливания свойств многомерной схемы Кули-Тьюки и комбинированного алгоритма составляет 40-73%. Снижение эффектив- ности с ростом числа процессоров связано с тем, что снижается доля одновременного вычисления частичных спектров, за счет которого и достигается основной эффект. Полученные результаты позволяют сделать вывод о том, что с ростом размерности преобразования при ограниченном числе процессоров, предпочтение должно отдаваться подходу, использующему структуру многомерной гиперкомплексной алгебры.

Работа выполнена при поддержке Министерства образования РФ, Администрации Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE); а также при поддержке Российского фонда фундаментальных исследований (РФФИ), проекты №№ 03-01-00736, 05-01-96501.