Алгоритмы фильтрации звуковых сигналов на основе U-преобразования

Задача очистки сигнала от шума с целью восстановления смысла сообщения, улучшения качества сигнала является одной из актуальных задач обработки сигналов. Часто предполагается, что на исходный сигнал действует аддитивная или мультипликативная помеха. В работе предлагается несколько алгоритмов фильтрации помех, основанных на U -преобразовании. Обзор алгоритмов фильтрации речевых сигналов приведен в [1].

Свойства U-преобразования

U -преобразование заключается в формировании многоуровневого (грубо-точного) представления сигнала с помощью фильтров Уолша системы Хармута [2-3], причем:

• -    для построения каждого уровня разложения используются фильтры одинаковой длины, которые масштабируются до размера анализируемого участка сигнала;

• -    сначала фильтры применяются ко всему сигналу, затем – к его частям.

Прямое U -преобразование записывается следующим образом: D = U ( S ), где D = { D_ij }, D_ij – j -ый спектр, находящийся на i -ом уровне разложения, i Е [0; J – 1], J – число уровней разложения, j е [0; M_i – 1], M_i – число элементов на i -ом уровне разложения.

Предлагаются следующие алгоритмы построения U -разложения исходного сигнала.

• 1.    Алгоритм формирования K -ичного дерева разложения сигнала (параметры алгоритма: J – число уровней разложения, K – число сегментов на i уровне, на которые разбивается сигнал на ( i – 1)-ом уровне), в вершине дерева расположено разложение исходного сигнала, M_i = Kⁱ – 1.

• 2.    Алгоритм построения разложения сигнала на одном уровне с использованием сегмента произвольной длины (параметры алгоритма: L – длина сегмента).

• 3.    Алгоритм построения разложения сигнала на одном уровне, при формировании которого сигнал разбивается на заданное число сегментов

(параметры алгоритма: M – число сегментов, на которое разбивается сигнал).

Вычисление спектрального представления каждого сегмента дерева H (или одного уровня разложения):

DM=T‘I1HMG»’»G [°;w-^

где G ' – набор фильтров, сгенерированный по фильтрам Уолша, W – число используемых фильтров, H_i = { H_i1 , …, H_{i Mi} } – множество сегментов, полученных из исходного сигнала S с шагом L на i -ом уровне разложения, H_ij – j -ый сегмент сигнала на i -ом уровне разложения, H_ij ( k ) – k -ый отсчет сегмента.

Обратное U -преобразование записывается как S' = U -1 [ D ], где S' – сигнал, полученный после выполнения обратного преобразования, U ^-1 – оператор обратного преобразования. Вычислить обратное преобразование можно следующим образом:

^-1

H^kVyMWY

4=0

где G – набор фильтров Уолша системы Хармута (см. рис. 1). Амплитуда анализируемого сигнала для выполнения операции восстановления должна быть нормирована к отрезку [0, 1] до построения разложения сигнала.

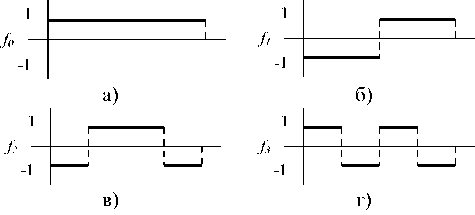
Рис. 1. Фильтры Уолша системы Хармута

Алгоритмы фильтрации данных

Рассмотрим предлагаемые алгоритмы очистки сигнала от шума. Алгоритм фильтрации №1 основан на обнулении коэффициентов разложения и состоит из следующих шагов.

• 1.    Построение U -разложения D сигнала S (формируется один уровень разложения, длина сегмента – L , L = W , W – число используемых фильтров).

• 2.    Модификация разложения D : обнуление в каждом спектре разложения указанных коэффициентов.

• 3.    Применение к модифицированному разложению D обратного преобразования: генерация сигнала S' .

Таблица 1. Варианты обнуления коэффициентов

№	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	0	0	0	0	1	1	1
2	0	0	1	1	0	0	1
3	0	1	0	1	0	1	0

8	9	10	11	12	13	14	15
0	1	1	1	1	1	1	1
1	0	0	0	0	1	1	1
1	0	0	1	1	0	0	1
1	0	1	0	1	0	1	0

Предположим, что разложение сигнала формируется с использованием 4 фильтров, тогда существует 15 (2 ⁴ – 1) комбинаций вариантов обнуления коэффициентов фильтров (см. таблицу 1).

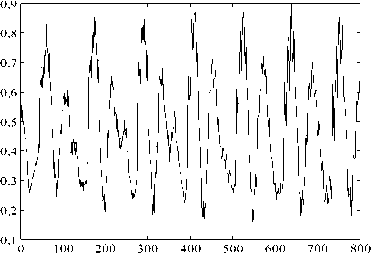
Рис. 2. Исследуемый сигнал

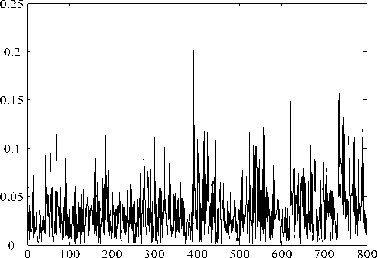
Рис. 3. Результат обнуления нулевого коэффициента

На рис. 3 показан сигнал S' (исходный сигнал показан на рис. 2), в каждом спектре которого обнулен нулевой коэффициент. Выполнение данной операции привело к потере информации о фор- ме сигнала (после обнуления сохраняется только высокочастотная составляющая сигнала).

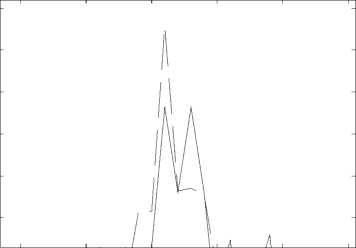
Таким образом, при решении задачи фильтрации обнулением коэффициентов нельзя использовать комбинации с первой по восьмую (см. таблицу 1). При использовании 10; 11 и 12 комбинаций в получаемые сигналы вносятся артефакты (см. рис. 3 и рис. 4, где сплошной линией показан восстановленный сигнал, пунктирной линией – исходный сигнал, отображается только часть сигнала). В данных комбинациях обнуляется первый спектральный коэффициент (см. рис. 1б).

0.6

0,5

0.4

0.3

0.2

0,1

50       55       60       65        70       75

Рис. 4. Результат восстановления сигнала с использованием комбинации 1001 (10)

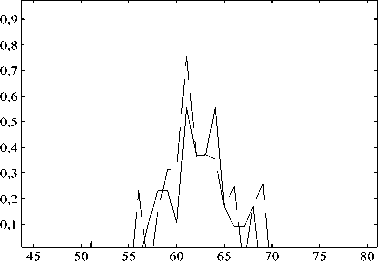
Рис. 5. Результат восстановления сигнала с использованием комбинации 1010 (11)

Можно отметить, что чем больше число знако-перемен(переходов черезноль)уфильтра,тембо-лее высокочастотную составляющую он позволяет выделить из сигнала. Количество информации о форме сигнала, находящейся в коэффициентах, уменьшается с увеличением числа знакоперемен в фильтре, генерирующем коэффициент. В связи с этим не рекомендуется обнулять спектральные коэффициенты, полученные с применением нулевого и первого фильтров, в противном случае это приведет не только к огрублению формы сигнала и сглаживанию шумовой составляющей, но и к внесению в сигнал различных артефактов.

Обнуление коэффициентов, полученных с применением второго и третьего фильтров, приводит только к «огрублению» сигнала после выполнения обратного преобразования. Сравнивая сигналы, полученные после применения 9 и 13, 14 и 15 комбинаций, можно отметить, что для 9 комбинации генерируется более грубый сигнал, чем для других комбинаций.

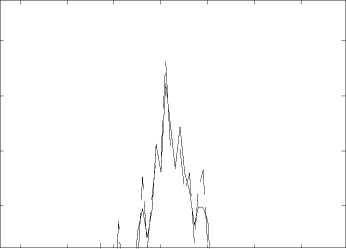
30     40     50     60     70     80     90

Рис. 6. Результат восстановления сигнала с использованием комбинации 1110 (15)

Таким образом, для фильтрации сигнала можно использовать следующие комбинации спектральных коэффициентов: 1000 (9), 1100 (13), 1101 (14), 1110 (15).

Выше проведен анализ результатов обнуления коэффициентов для 4 фильтров. При использовании большего числа фильтров будет доступно больше вариантов комбинаций обнуляемых коэффициентов. В результате выполнения алгоритма уровень шума в сигнале S' должен быть меньше уровня шума в исходном сигнале S . Указанный результат достигается за счет обнуления коэффициентов разложения, несущих информацию о высокочастотной составляющей сигнала, а следовательно, и о шуме.