Алгоритмы формирования интегральной OLAP-модели предметной области

Эффективность оперативной аналитической обработки данных на основе технологии OLAP (On-Line Analytical Processing) во многом определяется адекватностью модели предметной области [1]. Как правило, для оперативной аналитической обработки данных создается набор локальных OLAP-моделей, представляющий собой фрагментарную аналитическую модель предметной области [2–4]. С точки зрения теории и практики интересно построение интегральной аналитической модели, объединяющей множество частных OLAP-моделей, позволяющей манипулировать всеми аспектами и характеристиками анализируемого процесса и охватывающей максимальное число решаемых аналитических задач.

Для построения интегральной аналитической модели предметной области предложен метод концептуального OLAP-моделирования на основе анализа формальных концептов, позволяющий строить интегральную OLAP-модель предметной области в виде формальной решетки многомерных кубов [5]. Реализация предложенного метода требует разработки алгоритмов поиска кубов-концептов на основе контекста предметной области и построения концептуальной решетки OLAP-кубов.

Существующие на сегодняшний день алгоритмы генерации формальных концептов подробно рассмотрены в работах [6–9]. Как правило, эти алгоритмы разработаны без учета требований быстродействия и не ориентированы на обработку объектов OLAP-анализа.

В данной работе предлагаются алгоритм поиска кубов-концептов и алгоритм построения концептуальной решетки кубов, позволяющие формировать интегральную OLAP-модель предметной области на множестве всех объектов анализа. Свойства концептуальной решетки дают возможность оперировать всеми объектами анализа и выявлять аналитические зависимости, что повышает эффективность оперативной аналитической обработки данных.

Метод концептуального OLAP-моделирования предметной области. Метод концептуального OLAP-моделирования основан на интеграции технологии оперативной аналитической обработки многомерных данных и анализа формальных концептов [5; 10; 11].

Согласно предложенному методу, интегральная OLAP-модель предметной области представляет собой концептуальную решетку многомерных кубов. Основу интегральной модели составляет множество объектов оперативной аналитической обработки данных: множество показателей F = { f 1 , f 2 , …, f m } и множество измерений D = { d 1 , d 2 , …, d n }. Количественные характеристики анализируемого процесса образуют множество показателей, аспекты анализа предметной области образуют множество измерений.

Между элементами множеств F и D определяется отношение сопоставимости R – возможность совместной аналитической обработки показателей и измерений; R с F х D , (f , d j ) e R , если показатель f i может быть проанализирован по измерению d j . Тройка ( F , D , R ), в соответствии с методами анализа формальных концептов [12], представляет собой формальный контекст K . Формальный контекст отражает знания эксперта об объектах анализа предметной области и о возможности их совместной аналитической обработки.

На основе формального контекста K определяется множество кубов-концептов по признаку сопоставимости объектов анализа.

Для произвольных X с F и Y с D определяется операция «штрих» следующим образом:

X' = { d e D | V f e X(fRd)};

• Y' = { f e F | V d e Y(fRd)}.

Пара ( A , B ), где A с F , B с D такие, что A = B' и B = A' , называется кубом-концептом контекста K . Множество A состоит из показателей одинаковой размерности, которые могут быть проанализированы по всем измерениям из B. Пара ( A , B ) – многомерный куб, полный относительно добавления показателей той же размерности и состава измерений. Это означает, что невозможно включить в такой OLAP-куб дополнительный показатель без уменьшения числа измерений, т. е. в рамках построенного формального контекста не существует других показателей, сопоставимых с тем же набором измерений. Множество показателей A представляет объем куба-концепта, а множество измерений B – содержание куба-концепта.

Множество всех кубов-концептов частично упорядочено отношением подкуб-надкуб: ( A 1 , B 1 ) < ( A 2 , B 2 ) если A 1 с A 2 и B 2 с B 1 . В этом случае будем говорить, что ( A ₁, B ₁) – подкуб ( A ₂, B ₂), а ( A ₂, B ₂) – надкуб ( A ₁, B ₁). Множество показателей надкуба включает множество показателей подкуба, а, в свою очередь, множество измерений подкуба включает множество измерений надкуба. Упорядоченное отношением подкуб-надкуб множество всех кубов-концептов образует решетку OLAP-кубов, которая представляет собой интегральную OLAP-модель предметной области.

Для реализации метода концептуального OLAP-моделирования разработаны алгоритмы поиска кубов-концептов на основе контекста предметной области и построения концептуальной решетки OLAP-кубов.

Алгоритм поиска кубов-концептов на основе контекста предметной области. Алгоритм поиска кубов-концептов на основе контекста предметной области представляет собой итеративную реализацию метода Крайеса [6].

Алгоритм поиска кубов-концептов заключается в пошаговом сравнении объемов ранее обнаруженных кубов-концептов с множеством показателей, доступных для совместной аналитической обработки с каждым из измерений контекста. Рассмотрим блок-схему алгоритма поиска кубов-концептов на основе контекста предметной области (рис. 1).

На первом шаге алгоритма множество кубов-концептов B ( K ) содержит точную верхнюю границу множества кубов-концептов (супремум) – куб-концепт ( F , Ø), где F – множество всех показателей контекста K.

Затем путем перебора измерений d j из D определяется множество показателей { d j } ' , доступных для совместной аналитической обработки с каждым измерением d j , и сравнивается с объемом A k куба-концепта ( A k , B k ) из B ( K ), где k = 1,| B ( K )|, где | B ( K )| – мощность множества B ( K ). При этом индекс j определяется, как max { j' | d j e B k } + 1 - следующий за максимальным индексом измерений из содержания B k куба-концепта ( A_k , B_k ).

Если сформированный объем { d j } ' и объем A_k существующего куба-концепта не пересекаются ({ d j } ' n A k = 0), то рассматривается следующее измерение. Если объемы совпадают ({ d j } ' n A k = A k ), то содержание B k куба-концепта ( A k , B k ) дополняется измерением d j и алгоритм переходит к рассмотрению следующего измерения. Процесс добавления измерений к содержанию ранее обнаруженного куба-концепта называется наполнением куба-концепта.

В случае когда объемы не совпадают и их пересечение не пусто, формируется потенциально новый куб-концепт ( A new , B new ), где A new = { d j } ' n A k , B new = d j и алгоритм переходит к проверке уникальности найденного куба-концепта.

Для проверки уникальности куба-концепта, путем перебора d_i из D определяется множество показателей { d i } ' , доступных для совместной аналитической обработки с каждым измерением d i , и сравнивается с объемом A new потенциально нового куба-концепта. Индекс i = 1, j - 1 при условии, что d i t B k .

Если все показатели A new могут быть совместно проанализированы с измерением d i , то объем A new найденного куба-концепта ( A new , B new ) не является уникальным и алгоритм переходит к сравнению объема A k куба-концепта ( A k , B k ) с множеством показателей { d j + 1 } ' .

Если A _new содержит хотя бы один показатель, который не может быть совместно проанализирован с измерением d_i , то объем A _new найденного куба-концепта ( A new , B new ) является уникальным относительно измерения d i и алгоритм продолжает проверку уникальности объема потенциально нового куба-концепта относительно измерения d i + 1 .

Уникальность объема A new потенциально нового куба-концепта относительно всех проверенных измерений d i означает, что B ( K ) не содержит куба-концепта с таким набором показателей.

Далее для найденного уникального объема A new определяется B _new, как объединение содержания B_k и измерений d_i . Проверенный новый куб-концепт ( A _new, B _new) добавляется в B ( K ) и алгоритм переходит к сравнению объема A k куба-концепта ( A k , B k ) с множеством показателей { d j + 1 } ' .

В ходе работы алгоритма осуществляется наполнение ранее найденных кубов-концептов и обнаружение новых кубов-концептов, которые подлежат дальнейшему наполнению.

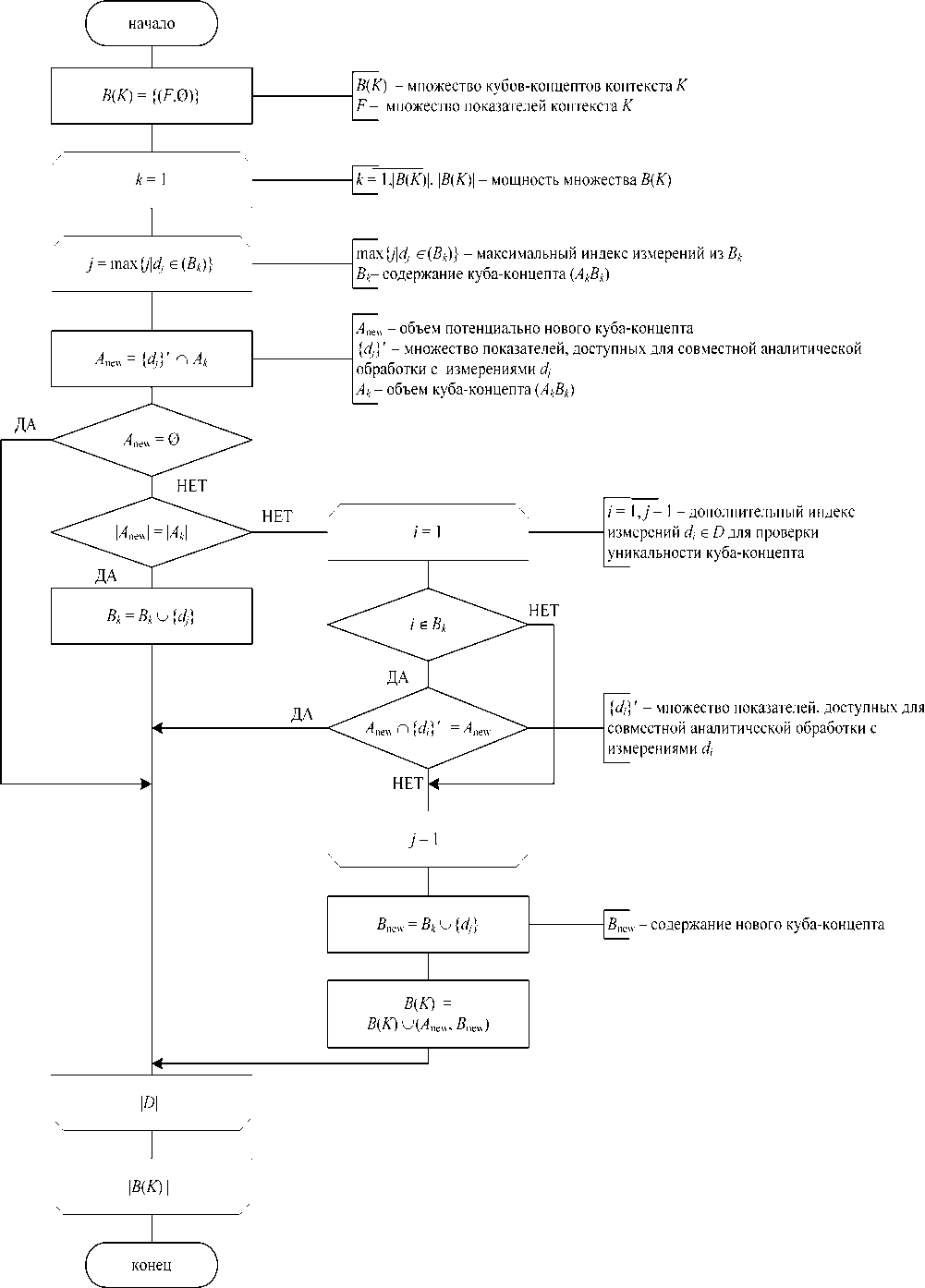
Рис. 1. Алгоритм поиска кубов-концептов на основе контекста предметной области

Все кубы-концепты контекста K считаются полными только по завершении работы алгоритма.

Таким образом, просматривая множество показателей и измерений формального контекста предметной области, формируется множество кубов-концептов .

Алгоритм построения концептуальной решетки OLAP-кубов. Алгоритм построения концептуальной решетки OLAP-кубов основан на алгоритме формирования концептуальной решетки NEIGHBORS [7 - 9] (рис. 2).

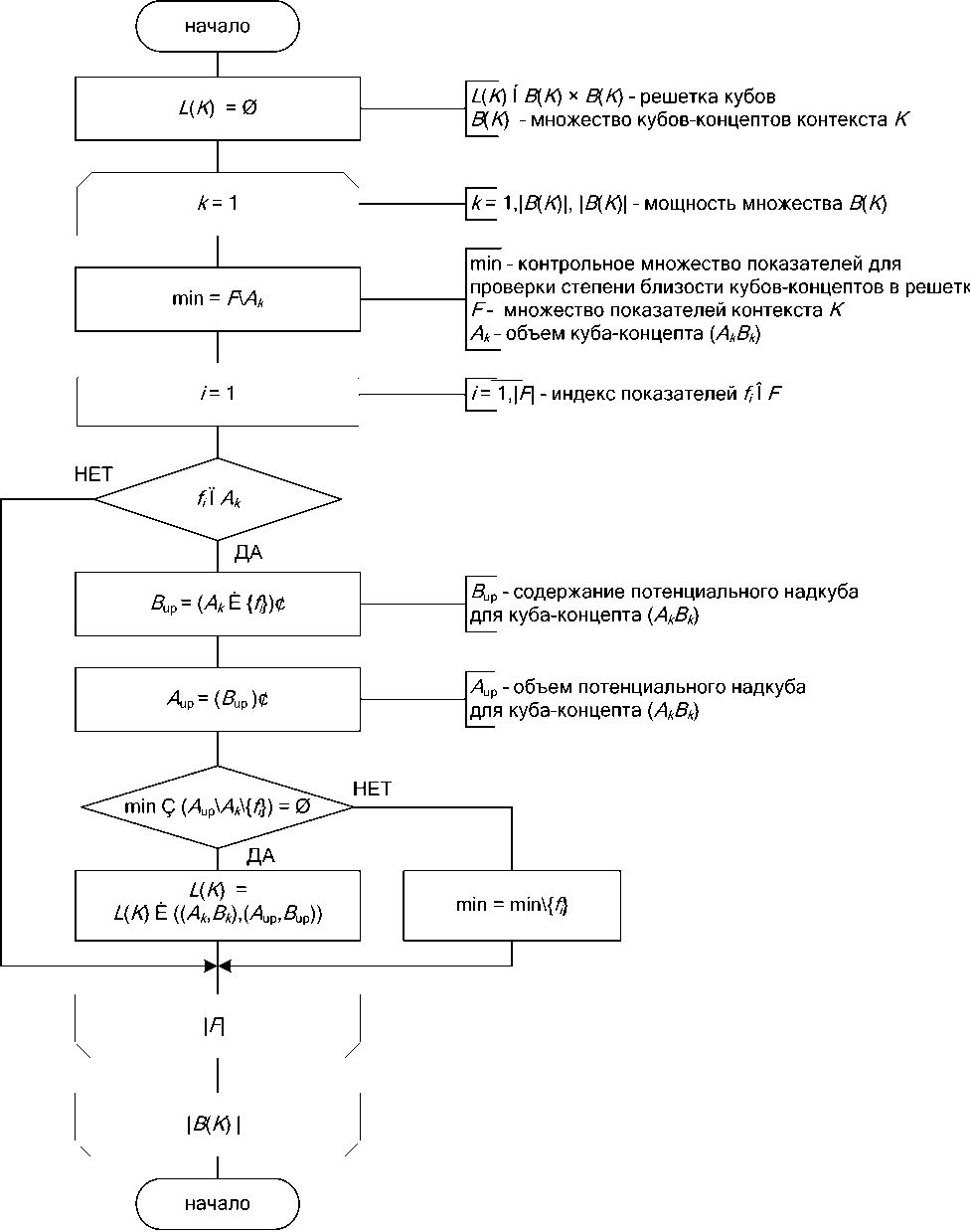
Рис. 2. Алгоритм построения концептуальной решетки OLAP-кубов

Задача данного алгоритма заключается в формировании пар кубов-концептов, находящихся в отношении частичного порядка подкуб-надкуб. Множество пар кубов-концептов из B ( K ) × B ( K ), упорядоченное отношением подкуб-надкуб, образует решетку OLAP-кубов L ( K ) ⊆ B ( K ) × B ( K ). Согласно методам анализа формальных концептов, свойства решетки такие, что если кубы-концепты X = ( A x , B x ) и Y = ( A_y , B_y ) находятся в отношении подкуб-надкуб X <  Y , то A_x ⊆ A_y и B_y ⊆ B_x . Исходя из данного свойства решетки, точная нижняя граница множества B ( K ) (инфимум) не имеет подкуба. Следовательно, алгоритм заключается в поиске надкубов для каждого куба-концепта ( A k , B k ) из множества B ( K ), начиная с инфимума и определении ближайшего надкуба, путем сопоставления объемов кубов-концептов.

На первом шаге алгоритма решетка кубов L ( K ) не содержит ни одной пары кубов-концептов из B ( K ) × B ( K ).

Затем для каждого куба-концепта ( A_k , B_k ) из множества B ( K ) определяется min = F\A k – контрольное множество показателей для проверки степени близости текущего куба-концепта и его потенциального надкуба.

Путем перебора показателей f i ∈ F , где i = 1,| F | при условии, что f_i ∉ A_k , формируется потенциальный надкуб ( A up , B up ) по следующему принципу: B up = ( A k ∪ { f i }) ' , A up = ( B up ) ' .

На следующем шаге с помощью контрольного множества min проверяется степень близости найденного потенциального надкуба к текущему кубу-концепту. Если объем A up потенциального надкуба помимо показателей из A k ∪ { f i } содержит другие показатели из множества min, то из контрольного множества исключается показатель f i , найденный потенциальный надкуб не является ближайшим для куба-концепта ( A k , B k ) и алгоритм переходит к рассмотрению следующего показателя f i + 1 ∈ F . Иначе, найденный куб-концепт ( A up , B up ) считается надкубом для ( A k , B k ) и пара (( A up , B up ), ( A k , B k )) добавляется в решетку L ( K ) и алгоритм переходит к рассмотрению следующего показателя f i + 1 ∈ F .

После рассмотрения всех показателей f i ∈ F алгоритм переходит к обработке следующего куба-концепта ( A k + 1 , B k + 1 ) из множества B ( K ).

Таким образом, перебирая все кубы-концепты и сопоставляя их объемы, определяются ближайшие надкуб и подкуб, которые образуют ребро концептуальной решетки кубов.

При изменении контекста предметной области, связанного с добавлением (удалением) объектов анализа или добавлением (удалением) отношения сопоставимости между показателями и измерениями, выполняется адаптация концептуальной решетки кубов по описанным выше алгоритмам поиска кубов-концептов и формирования решетки OLAP-кубов.

Формирование интегральной OLAP-модели научной деятельности организации. Разработанные алгоритмы поиска формальных кубов-концептов и построения концептуальной решетки кубов применены для формирования интегральной OLAP-модели научной деятельности организации.

Исследование отчетных форм и решаемых аналитических задач позволяет эксперту сформировать множество терминов предметной области и на их основе определить объекты анализа:

– множество показателей – число публикаций; число патентов; число статей; число учебных пособий; число грантов; число проведенных конференций; количество сотрудников и т. д.;

– множество измерений – год; подразделение; тип пособия; город; название журнала; тип публикации; тип патента; статус конференции; автор и т. д.

С учетом сопоставимости показателей и измерений построен формальный контекст научной деятельности, который отражает знания эксперта об объектах анализа и возможности их совместной аналитической обработки. В контексте определены следующие элементы множества F = { число публикаций , число проведенных конференций , число патентов , число стат е й , число учебных пособий } и элементы множества D = { год , подразделение , тип пособия , город , название журнала , тип публикации , тип патента , статус конференции , автор }. Используя сокращенные обозначения, получены соответственно: F = { f ₁, f ₂, f ₃, f ₄, f ₅} и D = { d 1 , d 2 , d 3 , d 4 , d 5 , d 6 , d 7 , d 8 , d 9 }.

С помощью алгоритма поиска формальных кубов-концептов на основе построенного контекста определены кубы-концепты. Для рассматриваемого контекста найдено 8 кубов-концептов (рис. 3).

Концептуальная решетка OLAP-кубов, построенная с помощью разработанного алгоритма, представляет собой интегральную OLAP-модель научной деятельности организации (рис. 4).

Разработанные алгоритмы поиска кубов-концептов на основе контекста предметной области и алгоритм построения концептуальной решетки кубов позволяют реализовать метод концептуального OLAP-моделирования и формировать интегральную OLAP-модель предметной области на множестве всех объектов анализа. Свойства концептуальной решетки обеспечивают возможность оперировать одновременно всеми объектами анализа и выявлять аналитические зависимости, что позволяет повысить эффективность оперативной аналитической обработки многомерных данных. Практическим результатом работы стало построение интегральной OLAP-модели научной деятельности организации на основе разработанных алгоритмов.

lib

PrX*lV

[По"у-*1Т6 K0f«4«1’Ы j

g    <*>*ал    oi    Ее     di   м    и     oto»1 г0*   Fb»M?*f'*e**«e Г^гахзбиа Гфс» Mi«#*v -УТ^Ч Tm r?|r<.-Mrev* Г*1 п->7*чт.1 iLf^rnjy * i  4w#i>6w»vt)    £     Е      Q     О      О       0      О      О # 2  чк. •»;•%•;«■ д<^«х ■ к> л  Е     £      □     И      О         П      СИ # 3  чс^б^геи'йй      £     £      □     □      С        □      И      □ R Чклойгвмм                £ ►    И '-ЙЕ чо 5леб№1. r>x :/'*»^^^J    £        И      й        П         Pl        П        П

в F1

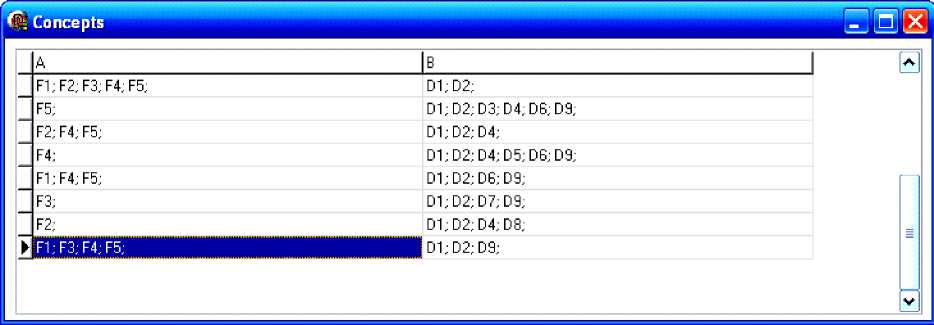
Рис. 3. Редактор формального контекста и сформированные кубы-концепты научной деятельности организации

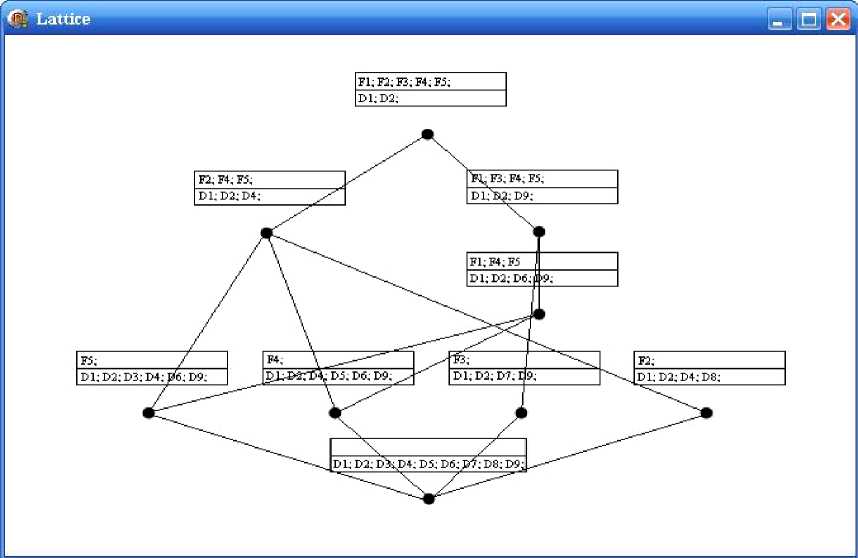
Рис. 4. Решетка кубов-концептов научной деятельности организации