Алгоритмы идентификации объектов в системах видеонаблюдения с использованием статистических методов

Некоторые задачи распознавания образов являются задачами статистической проверки гипотез. При этом аналитические решения получены для тех задач, вероятностные характеристики которых описываются с помощью членов экспоненциального семейства. В их число входят нормальное, экспоненциальное, релеевское, пуассоновское и многие другие известные распределения [1]. Однако во многих случаях члены экспоненциального семейства с их плавными изменениями и однообразием формы не дают хорошего приближения реально встречающихся плотностей. Использование не приближенных, а действительных плотностей распределения приводит к ситуации, что полученный алгоритм сложно реализовать на практике, так как он может потребовать больших объемов памяти и высокого быстродействия. Для преодоления этой сложности условную плотность вероятности предложено задавать не в аналитической форме, а в виде таблицы.

Алгоритм максимального правдоподобия

Алгоритм максимального правдоподобия (МП) очень часто используется для классифика-

ции и для оценки неизвестных параметров. Он

имеет вид [2]:

к = arg max p(x | H,)

где Hi – гипотеза, соответствующая классу l ; P^- | H, ) – плотность вероятности наблюдаемого сигнала x при условии, что справедлива гипотеза Я,; H- – решение, которое выносит классификатор.

P^ I ^Hi ) = p(-^Yi, ^x2-^xd I ^Hi ) = П p(^xi \Н,\ (2)

С учетом выражений (2) и (3) алгоритм МП примет вид:

к = arg max

пХ1, Iя/) ■

Если ^!я/) не является членом экспоненциального семейства, то аналитическое выражение для П*,1Я/) будет иметь достаточно сложный вид. Кроме того, вычисление произведения представляет собой операцию, которая требует высокого быстродействия. Для решения этой проблемы воспользуемся двумя приемами.

Во-первых, вместо произведения будем вычислять логарифм от него, поскольку логарифм – это монотонная возрастающая функция, которая не влияет на операцию вычисления аргумента максимума:

к = arg max П p^Xj \Ht) , к = arg max

/

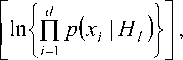
21п[р(-х, Iя/)] •

к = arg max

Во-вторых, если переменная X может принимать только дискретные значения (такое предположение верно при использовании цифровых

сигналов), то функцию 1п[Цл:|Я/)] для каждого из l классов можно задавать не в аналитическом виде, а в виде таблицы. Тогда, принимая последовательность *1^2-^ , можно вычислить выражения ЬпШя,)] и принимать решения 7=1

согласно алгоритму МП. Ниже приведены примеры задач, которые решаются с использованием алгоритма МП. В первой задаче производится классификация объектов (см. рис. 1), а во второй – оценка неизвестного параметра (см. рис. 5).

2 Идентификация дорожной разметки

На автомобиле установлена видеокамера, которая производит съемку автотрассы. Необходимо по полученному изображению идентифицировать дорожную разметку, которая нанесена белой краской (см. рис. 1а). Эту задачу можно рассматривать как различение двух классов: первый класс соответствует «белой» разметке на дороге, второй класс соответствует «серому» асфальту дороги. Соответственно, можно анализировать фрагмент изображения, рассматривая яркость пикселей этого фрагмента, и принимать решение, к какому классу принадлежит этот фрагмент.

Для вывода алгоритма можно воспользоваться следующей моделью:

x = 6,-b + (l-6>)-f + n, (5)

где X – это значения яркостей пикселей внутри фрагмента изображения; b – это значения яркостей пикселей, которые соответствуют «серому» асфальту; f – это значения яркостей пикселей, которые соответствуют «белой» разметке; 0 = 1, если верна гипотеза H 5 соответствующая «серому» асфальту; 0 = 0, если верна гипотеза H j , соответствующая «белой» разметке; n – помеха.

Рис. 1. Автомобильная трасса (а), результат идентификации дорожной разметки (б)

Положим, что фрагмент содержит d пикселей, то есть х = Ц_|,л:₂..^)^т, b = (Z?₁,Z>₂..^)^T, f Ч/рЛ-Л/Г, n = (»P«2-«J . Из-за воздействия внешней среды не все пиксели фрагмента будут одинаковой яркости. Так, краска, которой отмечают разметка, облупляется и выгорает на солнце. Отдельные фрагменты асфальта отличаются оттенками серого, кроме того, они могут изменить оттенок цвета из-за грязи и мусора.

Исходя из этих предположений, можно предположить, что яркость одного пикселя, который соответствует асфальту, может принимать значение из некоторого диапазона яркости [^min ’ bb L который соответствует «серым» оттенкам цвета с вероятностью Pb ’ близкой к единице, и может принимать значение из некоторого диапазона яркости \^b ’ ^max ] ’ который не соответствует «серым» оттенкам с вероятностью 1 - pb . Это выражается записью gb^='

r-^TT’^^’ ^max ^b

TT^’^^-

^b ^min

^’ ^b ^ [^min ’ ^max J

График §b (^) представлен на рис. 2.

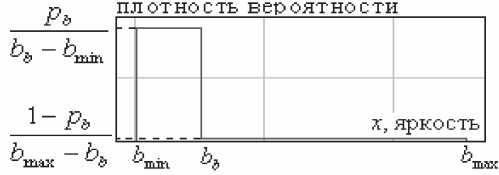
Рис. 2. Плотность вероятности §b

Аналогичные рассуждения можно повести для фрагмента изображения, соответствующего белой разметке: яркость одного пикселя, который соот- ветствует разметке, может принимать значение из некоторого диапазона яркости [.//? ) .Утах ] ’ который соответствует «белым» оттенкам цвета с вероятностью р f, близкой к единице, и может принимать значение из некоторого диапазона яркости V™.Jb\ который не соответствует «белым» оттенкам с вероятностью ^-рпчто выражается записью:

Pf

ф

ф

-ф

<7„

-ф

Pf

§М=‘

\-pf

Графики плотностей вероятностей рД I ^Hi,) и Дх | H_f ) представлены на рис.4.

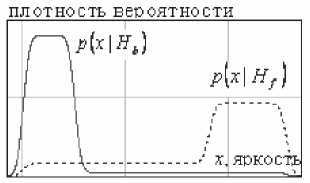
Рис. 4. Плотности вероятности P(^X\^Hb)

График функции g / О ) представлен на рис.3.

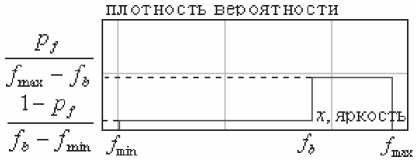
Рис. 3. Плотность вероятности g f^P

Плотность вероятности помехи n на одном пикселе изображения положим нормально распределенным:

и

Так как решение принимается не по яркости одного пикселя, а по всем яркостям пикселей фрагмента ^x^^^xl•■^xd, то

d

р(х,,х₂ ,.x_d Iя_й) = П Р^ \нД,

\=—exp - 2л-(7„      „

n- '

2ф; .

Аналитическое выражение для вычисления

П^к |я6) усложняется уже при (7 = 2:

где CF_H – среднеквадратическое отклонение (СКО) помехи. Найдем плотность вероятности pk^x I H_b) для значения яркости одного пикселя X при условии, что справедлива гипотеза Я_b, то есть если x = b + n . Чтобы найти плотность вероятности суммы случайных величин, положим, что величины являются независимыми, и воспользуемся соотношением [4]:

V

х²(^тах "^ЪЬ>

Ф

x2 - bb

-Ф

Pb ^bb -b_m™

.2 Л

'"Рь

Pb

Ж - Z>_min)

exp -

2(7,;

dz +

Ф

Ф

-Ф

2(^тах -ЬД

Ф

Ь

-Ф

-Ф

2^max - ЬЬ )

Ьь ^ma,x ^b

exV^.

dz =

Pb

2(^6 - ^min )

Ф

•^1 ^min

-Ф

^1 -b_b

где

²(^тах -ЬД

Pb

2(^6 -^тт)

ф

Ф

ь

-ф

x-bmm

t

• jexp-- \dt o 2 I

Аналогично для Р^^Х I ^H f )

-V-^max

-Ф

– функция Крампа.

можно получить

Ф

Pb

^Ьь -^min)

Ф

-Ф

Ф

-Ф

-Ф

Упростить это выражение не удается, а при d = 3 оно становится еще более громоздким. Похожий результат можно получить и для пН^1^я/)- Поэтому можно воспользоваться м табличным методом.

На рис. 1б представлен результат идентификации дорожной разметки, где черным цветом помечены области, которые были идентифицированы как «разметка».

Оценка фона для обнаружения движущихся объектов

Жестко закрепленная камера снимает участок автомобильной трассы для определения местоположения движущихся объектов на изображении. Эта задача является известной, и алгоритмы, решающие ее, получили название «background subtraction», то есть в буквальном переводе «вычитание фона», так как, перед тем как определить местоположение движущихся объектов, необходимо предварительно оценить фон.

В некоторые моменты времени отдельный пиксель изображения отображает фон, в другие моменты времени он заслонен проезжающими автомобилями. Можно заметить, что яркость фона представляет собой медленно меняющуюся во времени величину, но если пиксель заслонен автомобилем, то яркость его будет определяться цветом проезжающего автомобиля (см.

рис. 5а). Если оценка яркости фона происходит по последовательности кадров, на протяжении которой яркость фона практически не меняется, то статистические характеристики яркости фона можно описать дельта-функцией.

Проезжающие автомобили могут быть различных оттенков яркости, и ни одному из градаций яркости нельзя отдать предпочтения. В этом случае плотность вероятности яркости движущихся объектов близка к равномерному распределению. События, что пиксель отображает фон или движущийся объект, являются случайными, и каждому из этих двух событий можно поставить в соответствие вероятности: р{Яу| – вероятность, что пиксель заслонен движущимся объектом; pH) – вероятность, что пиксель отображается фон. Положим, что шум на изображении является гауссовым. Исходя из этих предположений, можно записать, что модель наблюдаемого сигнала яркости X будет:

х^е-ь^^-оу ji+n, (10)

х^ – яркость пикселя изображения в момент времени i; 0 = \, если верна гипотеза Нь ? соответствующая фону; 0 = 0 если верна гипотеза Н у , соответствующая движущемуся объекту; n – помеха. Соответствующие вероятностные характеристики:

Рис. 5. На последовательности кадров пиксель изображения отображает то фон, то заслонен автомобилем (а), результат оценивания фона видеоизображения (б)

p(b)=S(b-mb);

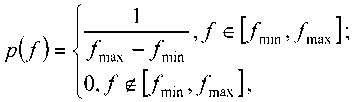
Как и в первом примере, аналитическое выражение для вычисления П/’U \ть усложняется уже при d = 2. Поэтому можно воспользоваться табличным методом для оценки значения mb согласно выражению mb = arg max

£1п(Р{я6}-/>(.7 \Hb,

mb

где m_b – яркость фона, которую необходимо оценить; cr – СКО шума; – минимальное и максимальное значение яркости, которые способна фиксировать видеокамера, соответственно.

Плотности вероятности при этом:

pV I ^нъ - ^ть ) = "7=— ^exP \2тга

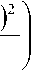
2(7,;

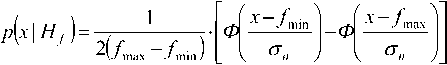
Плотность вероятности P^^x I ^mb ) представляет собой смесь двух распределений: рк^х\^нъ^Ч^ и p{^X\^Hb) и определяется выражением [1]:

PU I ™b ) = ^PK } • P^^x I ^ны ^mb ) + ^Р{^я/}¹ X^х I^я/)

График плотность вероятности P^^x I m_b ) представлен на рис. 6.

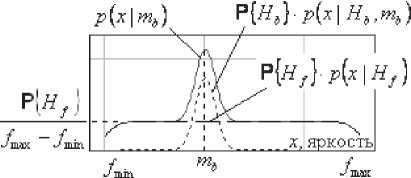
Рис.6. Плотности вероятности P\^x I m_b

Задачу оценки яркости фона mb для пикселя изображения нельзя решить, если использовать только одно значение яркости с одного кадра видеоизображения, так как результаты оценки будут недостоверными. Поэтому для оценки яркости элемента изображения заднего плана используют несколько кадров (d кадров), когда для каждого пикселя изображения известны d предыдущих значений яркости XVX2-Xd, тогда алгоритм МП для оценки яркости фона mb запишется в виде mb = argmaxfp^j,.^.^ | mJ} =

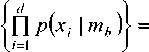
= arg max ^mb

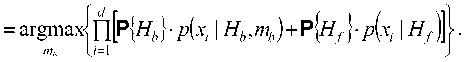
+ ^р(^я/ }• pk^xi I ^H f))]

^^ньУ P^x\Hb^mb

)+р{я/}-/?(л-|Я/)]

для каждого из mmP«b2-^mbL значения. По

^Х1 ’ ^X2 v^xd вычисляются значения

X 1п(р{я_б} • p^Xj I H_b, m_b ) + р{я _f }• p^Xj \H_f^. /=1

Выбирается такое значение m_b = ^ть (где ^mb принимает одно из значений m_bX,m_b,..m_bL ), для которого выражение

^\х\^^Н_ьУ р^хДН_ь,т_ь^^\н _f\ P^i I^я J) /=1

будет принимать максимальное значение. Полученное значение ^b берется в качестве оценки яркости фона для одного пикселя изображения. Результат оценки фона представлен на рис. 5б.

Заключение

Для решения задач распознавания образов могут быть использованы статистические методы, при этом те решения, которые не могут быть получены аналитически, могут быть получены с использованием табличных методов.