Алгоритмы координационного управления комплексной безопасностью объектов критического применения

Одно их основных направлений развития народного хозяйства Российской Федерации связано с ужесточением требований к обеспечению безопасности объектов критического применения (ОКП). Типичными примерами таких объектов являются атомные энергетические комплексы, химически-опасные производства, учреждения министерства обороны, внутренних дел и уголовно-исполнительной системы, отраслевые, территориальные и общегосударственные коммуникационные и логистические системы. При этом надлежащий уровень их безопасности должен обеспечиваться не только «силовыми» способами, но главным образом за счет повышения эффективности управления по всем аспектам вероятных угроз [1; 3; 12; 13].

Как показывает анализ, эта проблема пока не получила должного решения. Как и ранее, управление безопасностью этих объектов осуществляется преимущественно по отдельным составляющим (техническим, экологическим, технологическим, информационным и др.), без учета их взаимосвязей и, практически, без применения математических средств интеллектуальной поддержки принимаемых решений. Вместе с тем системы управления безопасностью ОКП все в большей мере приобретают черты интегрированных территориально распределенных человеко-машинных комплексов с постоянно расширяющимся набором функциональных подсистем, в частности таких, как контроль доступа; пожарная сигнализация и пожаротушение; обеспечение жизнедеятельности и информационной безопасности. Эти подсистемы, будучи вероятными объектами деструктивных воздействий со стороны разного рода правонарушителей, оказываются связанными через технические, электронные, инфраструктурные, территориальные и иные ресурсы. Возникают конфликты интересов, применительно к которым традиционные методы поиска оптимальных решений теряют свою конструктивность.

Следует отметить, что общетеоретические вопросы управления многоуровневыми иерархическими системами с многоаспектными связами компонентов получили освещение в исследованиях как зарубежных (М. Месарович, Д. Мако, И. Такахара), так и отечественных ученых: В.Н. Бурков, Д.А. Новиков, Д.С. Конторов, В.И. Новосельцев. Вместе с тем конкретные вопросы оптимизации управления комплексной безопасностью ОКП, доведенные до уровня их алгоритмизации, пока остаются нерешенными.

Цель статьи заключается в разработке алгоритмов оптимизации процессов управления комплексной безопасностью ОКП, обладающих указанными выше свойствами. Исследования базируются на положениях теории управления организационными системами [5; 7], дополненных элементами теории конфликта [2; 6; 8; 12] и методами координационного управления [4; 10; 14].

Формулировка задачи управления комплексной безопасностью ОКП

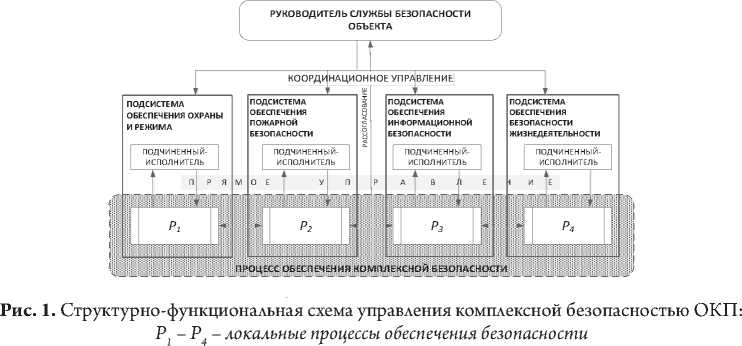
В качестве исходной примем структурно-функциональную схему управления комплексной безопасностью ОКП (рис. 1).

Как видно из этой схемы, безопасность в ОКП представляет собой комплексную категорию, включающую: безопасность режима и охраны, пожарную безопасность, информационную безопасность, безопасность жизнедеятельности (в том числе безопасность инженерных сооружений, здоровья и жизни людей). При этом специфика управления заключается в том, что лица, принимающие управленческие решения по названным локальным аспектам безопасности, наделены определенной самостоятельно-

88 в ыпуск 2/2020

стью. Не только исключение, но любое ущемление этой самостоятельности снижает уровень безопасности объекта, поскольку сопровождается снятием ответственности с подчиненных при выполнении ими своих функциональных обязанностей. Вместе с тем самостоятельность в принятии решений приводит к конфликтам «руководитель – подчиненный» и «подчиненный – подчиненный», что также отрицательно сказывается на безопасности объекта.

Для описания качества функционирования функциональных подсистем введем систему локальных показателей (табл. 1).

Таблица 1

Локальные показатели, используемые при управлении функциональными подсистемами безопасности ОКП

Показатели	Описание
Показатели режима и охраны ( h )	q 11 – уровень безопасности при проведении специальных мероприятий; q 12 – уровень охраны объекта; q 13 – уровень личной безопасности сотрудников и спец. контингента; q 14 – своевременность выявления и ликвидации критических ситуаций, связанных с действиями злоумышленников и террористов; q 15 – уровень контроля режима секретности и допуска
Показатели пожарной безопасности ( ^ 2 )	q 21 – уровень соблюдения требований пожарной безопасности; q 22 – уровень обеспеченности объектов средствами пожаротушения; q 23 – уровень обученности личного состава действиям на пожаре; q 24 – уровень противопожарного состояния объектов; q 25 – уровень организации и управления пожарной безопасности; q 26 – уровень потенциальной опасности возгорания объектов; q 27 – своевременность выявления и ликвидации пожаров
Показатели информационной безопасности ( q 3 )	q 31 – надежность предоставления информации; q 32 – полнота выходной информации; q 33 – своевременность предоставления информации; q 34 – достоверность выходной информации; q 35 – сохранение конфиденциальности информации; q 36 – уровень защищенности от несанкционированного доступа; q 37 – своевременность выявления и ликвидации критических ситуаций, связанных с информационной безопасностью

Орлова Д.Е. Алгоритмы координационного управления...

Окончание табл. 1

Показатели	Описание
Показатели безопасности жизнедеятельности ( ^ 4 )	q 41 – уровень экологической безопасности; q 42 – уровень безопасности инженерных сооружений; q 43 – уровень гигиены и оказания медицинской помощи; q 44 – уровень обеспечения питанием; q 45 – своевременность выявления и ликвидации критических ситуаций, связанных с опасностью жизнедеятельности

( i = 1,4 ) - векторы

Введем в рассмотрение вектор-функции qt = <|i (mi, yt, t), где mi управлений внутри функциональных подсистем, а yt (i = 1,4) -

векторы управления

функциональными подсистемами. Предположим, что все векторные пространства линейные, а оси их координат нормированы в диапазоне [0,1]. Также будем предполагать, что все показатели безопасности находятся в интервале [0,1], а их максимальные значения равны единице.

Тогда задачу управления комплексной безопасностью ОКП можно сформулировать в виде совокупности взаимосвязанных оптимизационных задач следующего вида:

Tr

A ( t ) = 1 J i ¹ - G [ § i ( t ) ,^§ 2 ( t ) , § з ( t ) , § 4 ( t ) ] } dt

_ T 0

^ min;

й e Y ‘

f [Si (t), §2 (t), S3 (t) ,§4 (t )] = 0, где Gr — годограф вектор-функции Г = ^[81 (t) ,82 (t), 83 (t), 84 (t)]; f [81 (t),82 (t), 83 (t), 84 (t)] = 0 - функция, отражающая связи между переменными 81 (t), 82 (t), 83 (t), 84 (t); T - интервал времени.

Г 1 rr                     )

S i ( t ) = -J[ ^{i -} G/^m i , y , t ) ] dt

V ¹ 0                         7

F i ⁽ q ii , ..., q 15 ) = ^0.

^ min;

m ^ e M _i

8 2 ( t ) =	( i Г г г                         ' - fl^ - G q y( m 2 , У 2 , t ) ] dt V 1 0                             z	^ ,^;
F 2 ( q 2i , .	.., q 27 ) = 0. ( i Ггг                  , ) m f [ i- G q 3 ( m 3 , y 3 , t ) ] dt v 1 0                          7 ., q 37 ) = 0. ( i Г г - J[ i — G q 4 ( m 4 , У 4 , t ) ] dt V 1 0
8 3 ( t ) = F 3 ( q 3i , .		^ min ; m 3 e M 3
8 4 ( t ) =		^ Д’
F 4 ( q 4i ,	.., q 45 ) = 0,	.

где G - ( i = 1,4 ) - годографы вектор-функций q i = q i ( rn _i , y , t ) ; i = 1, 4; F ij ( q ij ) = 0 функции, отражающие связи между q _ij .

–

90 в ыпуск 2/2020

Содержательная сторона задач (1)–(2) сводится к тому, чтобы руководитель слу жб ы безопасности объекта выработал и довел до подчиненных такие управления y _t ( i = 1,4 ) , которые, с одной стороны, обеспечивали бы максимально возможный интегральный эффект на уровне безопасност и объекта в целом, а с другой стороны, позволяли оптимизировать управления m. ({ = 1,4 ) локальными процессами обеспечения безопасности.

Основная трудность решения такой задачи заключается в наличие связей между переменными 8 1 ( t ) , 8 2 ( t ) , 8 3 ( t ) , 8 4 ( t ) . Это означает, что, приступая к решению любой из задач поиска оптимума, нужно иметь результаты решения всех других задач. В итоге получается замкнутый круг, для выхода из которого предлагается:

• а)    перейти от решений чисто оптимизационных задач к задачам координационного типа, в которых вместо детального учета связей между переменными 8 1 ( t ) , 8 2 ( t ) , 8 3 ( t ) , 8 4 ( t ) используется интегральная оценка связей, задаваемая матри-

• цей αij ,

компоненты которой характеризуют уровень взаимовлияния i -го и j -го аспекта

безопасности ( i , j = 1,4 ) ;

• б)    произвести типизацию моделей координационного управления по признаку

опасности ситуации и перейти к разработке не универсального, а типовых алгоритмов координационного управления.

Из сказанного следует, что задача управления комплексной безопасностью ОКП сводится к решению трех задач:

• •    оценка уровня рассогласованности локальных аспектов безопасности;

• •    типизация и выбор модели координационного управления, соответствующей степени опасности ситуации вокруг защищаемого объекта;

• •    разработка алгоритмов координационного управления ОКП, сообразуясь с выбранной моделью и трактуя ^ ( i = 1, 4 ) как вектор не прямых, а координирующих управлений.

Оценка уровня рассогласованности локальных аспектов безопасности

Рассогласованность будем трактовать как результат конфликта интересов между функциональными подсистемами, образующими систему обеспечения комплексной безопасности ОКП [2]. Тогда в качестве исходной базы такой оценки можно использовать следующую типологию (табл. 2).

Таблица 2

(d G, ) (a G ) |—qi- < о|л qj < 01 I agя_ I I agя J

—У ( a j — — 1,о ) — для «НТ»;

Типология рассогласований локальных аспектов безопасности

Тип	Форма проявления
Негативное («НТ»)	Подсистемы оказывают отрицательное влияние на функционирование друг друга
Позитивное («ПЗ»)	Подсистемы оказывают положительное влияние на функционирование друг друга
Позитивно негативное («ПН»)	Подсистемы оказывают как положительное, так и отрицательное влияние на функционирование друг друга
Нейтральное («Н»)	Подсистемы не оказывают влияние друг на друга

Тогда для оценки α _ij можно использовать следующие импликации:

Орлова Д.Е. Алгоритмы координационного управления...    91

⁽ d G,

1 ^™

) (6 G q.

)

a j = 1,0 ) ^- Для «ПЗ»;

^f d G,

^™

) fd G q

)! ГГd G

^™

) f d G q     )

a j =- 0,5 ) ^- Для «ПН»;

( ⁸ G ⁴

I — ^q- = 0

I d G ч

1 ( d Gq. 1 ( 8 G ) |л — j = 0 v I —-^J (d G_qi ^J (d G q

^™

1 ^{r 5} S

= 0 |л — j = 0

J Id G _q ..

qi

a ij = 0 ) — Для «Н».

Используя результаты расчетов по формулам (3)–(6), составляем матрицу 4×4 α _ij ; a ii = 0, по которой определяем средний, максимальный и минимальный уровень рассогласованности локальных аспектов безопасности:

--^'

4 (  4

a=^Z Z«

_ i = 1 V j = ¹ ( i * j )

ji

YI J;

a = min I min a .., min a .. I ; max                            ij ,

V ij a min = max max a , max a ji

.

V ij

Выбор модели координационного управления

При решении этой задачи будем исходить из того, что в ОКП принято выделять три типа ситуаций [11; 15]: критические, штатные и угрожающие. Соответственно, будем выделять три типовые модели координационного управления: в критических ситуациях (КС); в штатных ситуациях (ШС) и в угрожающих ситуациях (УС). Различие между этими моделями состоит в следующем. При координационном управлении в КС руководитель службы безопасности объекта берет на себя всю ответственность по обеспечению безопасности учреждения, отдает команды исполнителям, а они принимают эти команды к неукоснительному исполнению. При координационном управлении в ШС руководитель разграничивает полномочия исполнителей, а последние управляют процессами локальной безопасности в рамках отпущенных им полномочий. При координационном управлении в УС часть функций руководитель берет на себя, а другую часть делегирует подчиненным. Выбор типа модели координационного управления будем увязывать с оценками α , a max и a min . Для этого оценочное пространство [ - 1,0 ^+ 1,0 ] разобьем на интервалы [ - 1,0 ^- 0,33 ) ; [ - 0,33 ^+ 0,33 ) ; [ + 0,33 ^+ 1,0 ] , а для выбора модели координационного управления будем использовать импликации:

• а)    для гарантированной оценки:

[ - 1,0 ^a max <— 0,33 ) ^ модель координационного управления в КС ;

• < [ - 0,33 ^a max <+ 0,33 ) ^ модель координационного управления в УС ;    (10)

[ + 0,6 ^ a _max ^ + 1,0 ] ^ модель координационного управления в ШС ;

92 в ыпуск 2/2020

• б)    для оптимистической оценки:

[ - 1,0 min <— 0,33 ) ^ модель координационного управления в КС ;

• - [ - 0,33 min <+ 0,33 ) ^ модель координационного управления в УС ;

  
  
  
  

[ + 0,6 < a min < + 1,0 ] ^ модель координационного управления в ШС ;

• в)    для средневзвешенной оценки:

[ - 1,0 <СС<— 0,33 ) ^ модель координационного управления в КС ;

• * [ - 0,33 <СС <+ 0,33 ) ^ модель координационного управления в УС ;

[ + 0,6 <Й <+ 1,0 ] ^ модель координационного управления в ШС .

Для учета фактора воздействия на систему безопасности со стороны злоумышленников будем руководствоваться следующим эвристическим правилом, неоднократно проверенным на практике: чем выше угроза безопасности, тем ответственнее должно быть решение по управлению системой обеспечения безопасности. Такому правилу соответствует импликация в высокий уровень угроз') ^ (гарантированная оценка^;

с средний уровень угроз^ ^ ( средневзвешенная оценка^ ;

(низкий уровень угроз) ^ ( оптимистическая оценка') .

С учетом сказанного алгоритм выбора модели координационного управления комплексной безопасностью ОКП выглядит так:

Шаг 1. Используя формулы (3)-(6), заполняем матрицу ||a J |; а_й = 0.

Шаг 2. По формулам (7)-(9) рассчитываем величины a , a max , a min и, основываясь на эвристических соображениях, оцениваем уровень угроз безопасности по градациям: 〈 высокий 〉 ; 〈 средний 〉 ; 〈 низкий 〉 .

Шаг 3. Используя импликацию (13), определяем разновидность оценки рассогласованности локальных аспектов безопасности: 〈 гарантированная 〉 ; 〈 средневзвешенная 〉 ; 〈 оптимистическая 〉 .

Шаг 4. Используя соответствующую импликацию (10)–(12), выбираем подходящую модель координационного управления, соответствующую степени рассогласованности локальных аспектов безопасности и уровню угроз со стороны злоумышленников.

Такой подход позволяет уйти от детального учета связей между локальными аспектами безопасности, что усложняло решение поставленной задачи, и перейти к типовым алгоритмам координационного управления.

Алгоритм координационного управления в критических ситуациях

В этом случае критерий принятия решений выражается целевой функцией (1), а алгоритм сводится к следующей итерационной процедуре:

Шаг 1. Задаем стартовый вектор ; р ^{( 0 )} е Y; ( i = 1,4 ) .

Шаг 2. Решаем (2), полученные m i * ^{( 0 )} и 5 ( ^{0 )} ( i = 1,4 ) запоминаем.

Шаг 3. Для 5^{( 0 )} ( i = 1,4 ) решаем (1), ; р * ^{( 0 )} ( i = 1,4 ) и А^{( 0 )} запоминаем.

Орлова Д.Е. Алгоритмы координационного управления... 93

Шаг 4. Если А ( 0 ) = 0 - задача решена, m * ^{( 0 )} и J * ( ° ) ( i = 1,4 ) признаются оптимальными. При А^{( 0 )} >  0 продолжаем решение задачи.

Шаг 5. Выбираем новый случайный вектор у ^{( 1 )} е Y ; ( i = 1,4 ) .

Шаг 6. Решаем (2), полученные m * ^{( 1 )} и 5 ( 1 ) ( i = 1,4 ) запоминаем.

Шаг 7. Для 5^{( 1 )} ( i = 1,4 ) решаем (1), у *^ ( i = 1,4 ) и А^{( 1 )} запоминаем.

Шаг 8. Если А^{( 1 )} = 0 - задача решена, m * ^{( 1 )} и y * ^{( 1 )} ( i = 1,4 ) признаются оптимальными. При А^{( 1 )} >  0 попытку считаем безуспешной и переходим к шагу 5. Поиск прекращаем после р безуспешных итераций добиться А^(ц) = 0, а задачу достижения требуемых уровней безопасности при имеющихся исходных данных считаем невыполнимой.

( ц ) U^A )

Величины А = min А и 3 i Ч i = 1,4 ) фиксируем и вместе с величинами q ij высвечиваем в соответствующих окнах выходного интерфейса (рис. 2) [9].

94 в ыпуск 2/2020

Алгоритм координационного управленияв штатных ситуациях

В этом случае критерий принятия решений выражается совокупностью целевых функций (2), а алгоритм сводится к итерационной процедуре:

Шаг 1. Решаем (2) в предположении, что координирующие управления отсутствуют.

Полученные m * ^{( о )} и 8 ^{( о )} ( i = 1,4 ) запоминаем.

Шаг 2. Если V_ ( 8^{( о )} = о ) - задача решена, m * ^{( о )} ( i = 1,4 ) признаются оптимальными.

В противном случае продолжаем решение задачи.

Шаг 3. Задаем стартовый вектор у ^{( о )} е Y ; ( i = 1,4 ) .

Шаг 4. Для 8^{( о )} ( i = 1,4 ) решаем (1), "у * ^{( о}^ ( i = 1,4 ) запоминаем.

Шаг 5. Для у*^ ( i = 1,4 ) решаем (2), m * ^{( 1 )}

Шаг 6. Если ^ ( З^{( о )} = о )

и

^ *(

– задача решена, m _i

5 ( 1 ) ( i = 1,4 ) запоминаем.

'^{(1 )} ( i = 1,4 ) при у * ^{( о )} ( i = 1,4 ) признаются

оптимальными. Если указанное условие не выполняется, переходим к шагу 1. Поиск прекращается после ^ безуспешных итераций добиться выполнения условия Y ( 8 ^(ц) = о ) , а задача достижения требуемых уровней безопасности при имеющихся исходных данных считается невыполнимой. Величины 8 i = min 8 ^(ц) ; ( i = 1, 4 ) и Д фиксируются, и вместе

ц с величинами qij высвечивается в соответствующих окнах выходного интерфейса, аналогичного рисунку 2.

Алгоритм координационного управления в угрожающих ситуациях

В этом случае критерий принятия решений выражается как целевой функцией (1), так и целевыми функциями (2), а алгоритм сводится к следующей итерационной процедуре:

Шаг 1. Задаем стартовый вектор ; у ^{( о )} е Y ; ( i = 1,4 ) .

Шаг 2. Решаем (2). Полученные mi^ и 8 ( ^{о )} ( i = 1,4 ) запоминаем.

Шаг 3. Для 8^{( о )} ( i = 1,4 ) решаем (1), у * ^{( о )} ( i = 1,4 ) и Д^{( о )} запоминаем.

Шаг 4. Если [д^{( о )} = о ] л ^ ( б ( ° ) = о )

- задача решена, у * ^{( 0 )} ( i = 1,4 ) признаются

оптимальными. Если указанное условие не выполняется, то продолжаем решение задачи.

Шаг 5. Выбираем новый случайный вектор у ^{( 1 )} е Y ; ( i = 1,4 ) .

Шаг 6. Решаем (2), Полученные п г * ^{( 1 )} и 5 ( 1 ) ( i = 1,4 ) запоминаем.

Шаг 7. Для 8^{( 1 )} ( i = 1,4 ) решаем (1), у * * ¹ ( i = 1,4 ) и А^{( 1 )} запоминаем.

Шаг 8. Если [д^{( 1 )} = о ] л V_ ( 8 ( 1 ) = о )

- задача решена, у ^ ¹ ) ( i = 1,4 ) признаются

оптимальными. В противном случае переходим к шагу 5. Поиск прекращается после

^ безуспешных итераций добиться выполнения условия |^А ^(ц) = о ^л

Г^ ( " ^{) =} о ) ,

а задача достижения требуемых уровней безопасности при имеющихся исходных данных считается невыполнимой. Величины 8 i = min 8 ^(ц) ; ( i = 1,4 ) и А = min А ^(ц) фиксируются,

Ц                              ц и вместе с величинами qij высвечивается в соответствующих окнах выходного интерфейса, аналогичного рисунку 2.

Орлова Д.Е. Алгоритмы координационного управления...    95

Определение количества итераций

Величину µ , фигурирующую в алгоритмах координационного управления, будем связывать с вероятностью пропуска глобального экстремума целевых функций (1) и (2). Пусть априори известно, что эти целевые функции имеют β минимумов, из которых (β – 1) принадлежит области ∆_ρ ∈ Y (ρ = 1, 2,.., β – 1), а один – ∆_β ∈ Y . Согласно приведенным выше алгоритмам произведем моделирование равномерно распределенной в области Y случайной точки µ раз. Обозначим через P вероятность попадания точки в область притяжения ∆_ρ , а через α Р (0 <  α < 1) – вероятность попадания в область притяжения ∆_β. Тогда, справедливо (β – 1) Р + α Р = 1, а вероятность пропуска глобального экстремума P ' = ( 1 -a P ) ^ч = ( 1 -а/р- 1 + а ) ^ . Задавая требуемое значение P ‘ , можно оценить величину ^*. В нашем случае при P' = 0,9 и в = 2 оказалось, что ^ = 150 - 200.

Тестирование алгоритмов координационного управления

Тестирование производилось путем проведения вычислительного эксперимента в предположении, что вектор-функции y _i = y i ( m i , y i , t ) и г = r [ 8 1 ( t ) , 8 2 ( t ) , 8 3 ( t ) , 8 4 ( t ) ] линейны по отношению ко всем своим переменным. При этом считалось, что алгоритм работоспособен, если за 150–200 итеративных циклов (µ), он позволяет получить устойчивые результаты, то есть результаты, имеющие не более чем 15% отклонение от среднего значения. Результаты вычислительного эксперимента представлены в таблице 3.

Таблица 3

Результаты тестирования алгоритмов координационного управления

Разновидность алгоритма	Минимум итераций для обеспечения сходимости	Отклонение от среднего при десятикратном повторении циклов, %
В критических ситуациях	100–110	9–12
В штатных ситуациях	80–90	8–10
В угрожающих ситуациях	120–130	10–12

Из анализа приведенных данных видно, что описанные алгоритмы работоспособны в указанном выше смысле. Причем выявлена следующая закономерность: чем проще алгоритм, тем за меньшее количество итераций получаются устойчивые результаты. Так, например, для самого простого алгоритма координационного управления в штатных ситуациях устойчивые результаты получаются примерно за 80–90 циклов, а случае самого сложного алгоритма координации в угрожающих ситуациях – за 120–130 циклов.

Заключение

Предложенныеалгоритмы координационного управления комплексной безопасностью объектов критического применения отличаются от существующих аналогов тем, что в них наряду с классическими оптимизационными моделями используются типовые модели координации в критических, угрожающих и штатных ситуациях. Они позволяют решать задачу в условиях, когда лица, принимающие управленческие решения по локальным аспектам безопасности, наделены определенной самостоятельностью и в то же время их решения взаимозависимы. Для эффективного применения предлагаемых алгоритмов необходимо соблюдение двух условий. Во-первых, исходная модель комп-

96 в ыпуск 2/2020

лексной безопасности должна отражать иерархическую структуру управления с взаимосвязанными локальными подсистемами безопасности, а сами локальные подсистемы должны представляться совокупностью частных показателей, подобных таблице 1. Во-вторых, при их реализации необходимо использовать линейные пространства и операторы преобразования, в противном случае их сходимость не гарантируется.