Алгоритмы маршрутизации для многоагентной системы

В классической теории искусственного интеллекта (ИИ) решение какой-либо задачи сводится к созданию интеллектуальной системы, называемой агентом, которая, имея в своем распоряжении все необходимые знания, способности и вычислительные ресурсы, способна решить некоторую глобальную проблему.

Многоагентные системы (МАС) – это направление искусственного интеллекта, которое для решения сложной задачи или проблемы использует системы, состоящие из множества взаимодействующих агентов. В таких системах агент владеет лишь частичным представлением о глобальной проблеме, ограниченными ресурсами и выполняет лишь конкретные, возложенные на него обязанности. Для решения сложной задачи необходимо использовать множество таких агентов и организовать эффективное взаимодействие между ними. Такой подход позволяет построить из отдельных агентов единую многоагентную систему. Затем требуется произвести декомпозицию задачи и распределить ее части между агентами. Распределение задач означает присвоение каждому агенту роли, сложность которой определяется возможностями агента [1].

Обзор существующих моделей построения распределенного ИИ

Одним из подмножеств распределенного искусственного интеллекта являются роевые алгоритмы. Под данным определением подразумевается целый ряд моделей, в которых агенты являются достаточно простыми по своему устройству. В основном, данные алгоритмы решают задачи многокритериальной оптимизации. К числу роевых алгоритмов можно отнести такие алгоритмы как:

• -    алгоритм стаи птиц;

• -    муравьиный алгоритм;

• -    метод роя частиц;

• -    пчелиный алгоритм;

• -    оптимизация передвижением бактерий;

• -    алгоритм светлячков.

Далее рассмотрим наиболее интересные для нашей задачи алгоритмы более детально.

Алгоритм стаи птиц

Стая птиц является хорошим примером роевого поведения. Стая движется плавно и скоординировано, как единое целое. В стае отсутствует лидер, и стая является интеллектуальной системой. Каждого члена стаи можно полагать агентом в МАС. Для каждого агента действует небольшой набор правил, соблюдая которые, система приобретает характер интеллектуальной. В стае птиц как раз-таки существует такой набор базовых правил. Стая кружит в небе. При этом птицы стараются находиться на определенном расстоянии друг от друга, чтобы с одной стороны избегать столкновений и, с другой стороны, не потеряться из виду. В случае если какая-либо птица находит пищу, она оповещает об этом всю стаю.

Последний тезис может показаться противоречивым, но в то же время является одним из важнейших для данного метода оптимизации. С точки зрения отдельной птицы, самостоятельное насыщение эффективнее, чем борьба за пропитание с сородичами. Данным вопросом занимаются многие социобиологи по всему миру. Наиболее популярным объяснением этому служит то, что такое поведение каждой особи в стае способствует лучшему выживанию стаи в целом. Именно на эту идею опираются алгоритмы, построенные по данной схеме.

В основном, источники пищи разбросаны случайно. В одиночку птицам гораздо труднее находить их, из-за чего часть популяции может погибнуть. Если же члены стаи сообщают друг другу об источниках пищи, шансы на выживание стаи в целом существенно повышаются. Таким образом, будучи неэффективным с точки зрения одной особи, такой алгоритм является наиболее приемлемым для стаи в целом.

Первым, кто реализовал модель поведения стаи птиц, был Крейг Рейнольдс. В 1986 году он создал компьютерную модель, которую назвал Boids. Для того, чтобы его модель имитировала поведение стаи птиц, он заложил в нее три простых принципа. Во-первых, каждая птица старалась избегать столкновения. Во-вторых, птицы старались находиться на одинаковом расстоянии друг от друга и следовать в одном направлении. В-третьих, если птицы находили источник пищи, то они старались известить своих собратьев об этом [3].

Изначально Крейг предполагал использовать свою модель в качестве визуальной имитации. Тем не менее, он также отметил, что модель может быть расширена добавлением в нее возможности поисков пищи и уклонения от хищников. Тем самым, модель может быть использована в имитационном моделировании.

Классический алгоритм роя частиц

Джеймс Кеннеди и Рассел Эберхарт были вдохновлены идеей Крейга и в 1995 году предложили алгоритм для оптимизации непрерывных нелинейных функций, который они назвали методом роя частиц (МРЧ).

Разработанный ими алгоритм моделирует многоагентную систему, где агенты-частицы двигаются к оптимальным решениям, обмениваясь при этом информацией с соседями.

Каждая частица хранит в себе локальное, собственное наилучшее, значение и глобальное, найденное группой в целом, имитируя тем самым мгновенный обмен сообщениями. Частицы равномерно распределяются по плоскости, в которой производится поиск решений. Направление и скорость каждой частицы на каждой итерации зависит от найденных оптимумов и выглядит так:

v n ⁺ 1 = v n ⁺ c 1 • rnd • ( P n - x n ) ⁺ c 2 • rnd • ( g - x n ),                                ⁽¹⁾

где v – вектор скорости частицы, c 1 , c 2 – постоянные ускорения, – лучшая позиция, найденная частицей, g – лучшая точка из пройденных всеми частицами, – текущее положение частицы, а rnd – случайное число от 0 до 1 включительно.

После перемещения в новую точку, в случае надобности, частица обновляет свои значения лучших глобальных и локальных точек. Далее алгоритм повторяется [4].

Помимо классического алгоритма роя частиц существует масса его модификаций. В настоящее время можно выделить несколько основных путей улучшения алгоритма.

Предложенные модели систем распределенного ИИ

Рассмотренные выше алгоритмы напрямую не решают задачи маршрутизации. Тем не менее, принципы их работы могут использовать в модели ИИ, решающей эту проблему. На основе проведённого анализа было решено создать модели МАС, решающие следующие задачи:

• 1.    нахождение маршрута из точки старта в точку выхода при неизвестном ландшафте;

• 2.    нахождение самой точки выхода и маршрута к ней.

Далее приведены две модели, решающие поставленные задачи.

Модель №1 «Обучаемая модель МАС»

Данная модель направлена на решение первой задачи. Использует принципы горизонтального переноса генов (ГПГ) и продукционную базу знаний с весами для обучения.

Параметры модели

• 1.    p1 – вероятность того, что агент выберет действие из БЗ, а не сгенерирует случайное действие;

• 2.    p2 – максимальная приемлемая разница между состояниями, вычисляемая следующим образом. Все схожие ячейки состояния убираются, а остальные суммируются. Каждая разница между ячейками имеет вес 1. Неизведанные ячейки принимаются за занятые;

• 3.    p3 – количество итераций до обмена агентами информацией;

• 4.    p4 – количество итераций до параллельного переноса ген агентами;

• 5.    p5 – радиус видимости агентов;

• 6.    p6 – вероятность мутации.

Память

• 1.    Каждый агент хранит свою текущую позицию.

• 2.    Каждый агент хранит исследованную им карту в виде списка координат и значений ячейки (пустая/занятая). В случае если ячейка неизвестна, она не находится в карте агента.

База знаний

База знаний (БЗ) хранит в себе слепки состояния окружающей среды и реакции на них в виде продукционной модели с весами. Каждому состоянию соответствует определенное действие, и у каждой такой записи есть свой вес. База знаний делится на три подгруппы:

• 1.    «Правила здравого смысла» – это правила, которые останавливают агента от совершения бессмысленных действий, например, попыток идти в стену и т.д.

• 2.    Правила, заложенные моделью поведения роевого интеллекта. Например, в подобную часть базы знаний можно заложить поведение классического роя частиц.

• 3.    Эмпирическая часть. Часть БЗ, в которую агент заносит свои, приобретенные во время функционирования, знания.

Логика работы эмпирической части базы знаний во многом зависит от функции, определяющей успешность проведенного хода. В данном случае, успешность проведенного хода зависит от количества новых, изведанных, клеток и эвристической оценки близости выхода.

Алгоритм действий

У каждого агента существует три основных цикла работы.

• 1.    Цикл хода;

• 2.    Цикл обмена информацией;

• 3.    Цикл параллельного переноса.

На каждой итерации цикла хода агент производит следующие действия:

• 1.    При помощи рецепторов снимает состояние среды. Состояние среды представляется в виде ячейки, содержащей в себе агента, и ее соседей. Количество этих соседей зависит от радиуса видимости агента.

• 2.    На основе полученного состояния агент выбирает наиболее подходящую реакцию. Здесь существует два варианта развития событий, каждый из которых может случиться, исходя из заданной величины случайности p1 .

• a)    Агент выбирает реакцию из БЗ. В этом случае, агент берет состояние, снятое рецепторами на текущем шаге, сравнивает с присутствующими в БЗ, и, если оно не превышает p2 , то применяет действие, соответствующее этому состоянию, если это возможно. В противном случае, ищет следующее совпадение.

• b)    Агент генерирует случайную реакцию и выполняет действие.

• 3.    Если последнее действие было успешно (например, улучшило фитнес-функцию или раскрыло много неизведанных ячеек), то снятое состояние и реакция на него записываются в БЗ.

На каждой итерации цикла обмена информацией агент:

• 1.    Просматривает, присутствуют ли в радиусе его видимости другие агенты.

• 2.    Если агенты есть, то отсылает им свою карту и получает карты соседей.

• 3.    Карты складываются, дополняя друг друга.

На каждой итерации цикла параллельного переноса гена агент:

• 1.    Просматривает, присутствуют ли в радиусе его видимости другие агенты.

• 2.    Если агенты есть, то агент выбирает партнера, кодирует свою эмпирическую часть БЗ и производит скрещивание.

Пример

Описание процесса параллельного переноса ген на примере модели с p5 = 2.

• 1.    У агентов выбираются записи из эмпирической части БЗ с наибольшим весом.

2. Для случая с радиусом видимости, равным двойке, соседних клеток будет 18.

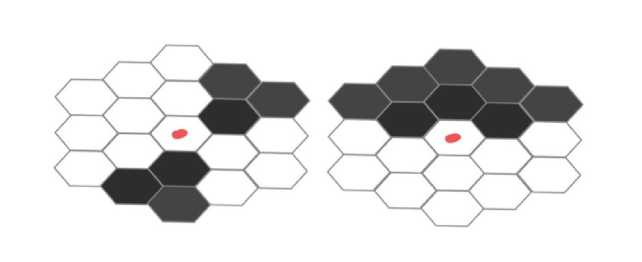
Рис. 1. Пример состояния, хранимого в БЗ

Далее происходит двоичное кодирование состояния из БЗ, и для данного случая будет использовано 18 бит. Ячейки считаются по часовой стрелке, начиная с самого дальнего уровня. В итоге получаются записи вида: 011000110000010100 и 111000000011110001. Затем случайно выбирается точка кроссинговера, и происходит скрещивание. Для полученных хромосом потомков из действий в БЗ, соответствующих родителям, выбирается действие. Происходит проверка допустимости выбранного перехода для данного состояния. В случае недопустимости происходит переход к шагу 1.

Выводы

Сложным местом данной модели является выбор фитнес-функции. От этого напрямую зависит успешность работы системы. Так, для достижения наиболее хороших результатов параметры радиуса видимости должны быть больше или равны 3, что обеспечит более адекватный результат. Еще одной интересной особенностью модели является привязанность обученной модели к топологии ландшафта, на котором она обучена. Поэтому при генерации ландшафта случайным образом обученная модель практически не имеет смысла. По-другому дело обстоит в случае, когда топология, хотя заранее и неизвестна, строится по подобным признакам. Благодаря этому можно считать, что обученная система уже изучила топологию, и исходя из этого проверять другие топологии на соответствие.

Модель №2 «Роевой алгоритм с координирующим агентом»

Данный алгоритм направлен на решение второй задачи – о поиске точки выхода и обладает простым поведением, присущим роевому интеллекту.

Описание

В данной модели задача поиска точки выхода декомпозирована на подзадачи, которые распределены между агентами. Агенты разделены на два типа. Первые – это агенты, собирающие информацию о неизведанной территории. Вторые – агенты-координаторы, их в модели может быть более одного. Последние являются статичными (неподвижными) агентами, выполняющими роль накопителей данных. Агенты, собирающие информацию, периодически возвращаются к агентам-координаторам и передают им всю накопленную информацию. От координаторов они, в свою очередь, получают всю имеющуюся у тех информацию. Тем самым обеспечивается постоянное наращение объема собранной информации. В данной модели присутствует специфичный термин «точка желания». «Точка желания» – это ячейка на локальной карте агента, при достижении которой агент может открыть какое-либо количество неизведанных ячеек.

Параметры

• 1.    p1 – количество исследованной территории до возвращения к координирующему агенту;

• 2.    p2 – вероятность выбора агентом непредпочтительной (по расстоянию до нее) следующей «точки желания»;

• 3.    p3 – радиус видимости агентов.

Память

• 1.    Каждый агент хранит свою текущую позицию.

• 2.    Каждый агент хранит исследованную им карту в виде списка координат и значений ячейки (пустая/занятая). В случае, если ячейка неизвестна, она не находится в карте агента.

• 3.    Каждый агент хранит в себе число пройденных достигнутых «точек желания».

Алгоритм действий

У каждого агента существует три основных цикла работы.

• 1.    цикл хода;

• 2.    цикл выбора новой «точки желания»;

• 3.    цикл обмена информацией с агентом-координатором.

На каждой итерации выбора новой «точки желания»:

• 1.    Агент перебирает все возможные области, граничные неизведанной территории, на локальной карте и из них случайным образом выбирает «точку желания». При этом каждый путь характеризуется весом, который зависит от расстояния между «точкой желания» и координатами агента. Поэтому, чем больше расстояние, тем менее предпочтительна «точка желания», но выбор ее все же возможен.

• 2.    Агент прокладывает путь от своей позиции до «точки желания» при помощи встроенного алгоритма поиска пути на известной карте (A*).

На каждой итерации цикла хода агент производит следующие действия:

• 1.    Из очереди шагов выбирается первый шаг, и производится переход.

• 2.    При помощи рецепторов снимает состояние среды. Состояние среды представляется в виде ячейки, содержащей в себе агента и ее соседей. Количество этих соседей зависит от радиуса видимости агента.

• 3.    Если агент встречается с каким-либо другим агентом, они делятся разведанной картой друг с другом. В случае если текущая «точка желания» агента уже была разведана другим агентом, он выбирает себе новую.

Существует два варианта развития событий, если агент нашел точку выхода:

• 1.    Если в точке выхода нет других агентов, то агент считает, что он первым нашел точку выхода, и возвращается в точку входа, чтобы сообщить координирующему агенту о найденной точке выхода.

• 2.    Если в точке выхода уже находятся другие агенты, то агент предполагает, что агенту-координатору уже известно о точке выхода, и агент встает в точку выхода.

Выводы

Данная модель показала достаточно хорошие результаты по количеству затрачиваемых итераций и способна в 100% случаев решить поставленную перед ней задачу. Модель может быть расширена и оптимизирована с помощью внесения динамически изменяемых параметров, таких, как p1 или же других изменений, обеспечивающих более высокую сходимость.

Заключение

МАС часто используются в задачах оптимизации, но в данной работе была проведена попытка применить аппарат МАС для решения задачи поиска выхода на неизвестном ландшафте (лабиринте).

В данной статье приведен обзор и сравнительный анализ существующих методов моделирования систем с распределенным ИИ, а также созданных на их основе собственных моделей. Модель, показавшая наиболее хорошие результаты – модель №2 с координирующим агентом. Алгоритмы, реализованные в данной модели, позволяют отыскать точку выхода и путь к ней, в случае существования пути. Достоинства данного метода:

• -  100% вероятность нахождения точки выхода и кратчайшего пути к ней, в случае ее достижи

мости;

• -    высокая скорость работы благодаря периодическому обмену информацией с координирующим агентом, что обеспечивает своевременное распространение суммарной информации;

• -    алгоритмы базируются на простых принципах, что не требует сложной аппаратной архитектуры в случае осуществления физической модели в реальном мире.

Недостатком данного метода является ограниченная область использования.

Для реализации предложенного метода была разработана программная система. Данная система позволяет:

• -    моделировать различные ландшафты;

• -    генерировать популяции МАС;

• -    наблюдать за ходом моделирования в реальном времени при помощи графического отображения модели.

Реализованная программная система может применяться в тестировании других методов и алгоритмов маршрутизации. Алгоритмы, созданные в данной работе, могут быть применены в работе медицинских «нанороботов», обнаруживающих, к примеру, холестериновые бляшки в кровеносной системе или в улучшенной навигационной системе для автоматизированных машин. В таком контексте предлагаемая разработка может пригодиться в военной промышленности, так как исключает обмен данными, а, соответственно, возможность какой-либо уязвимости в момент полевой инициации связи.