Алгоритмы математического моделирования трехмерных нестационарных температурных полей прецизионных приборов авиакосмического назначения

Задача исследования тепловых процессов, возникающих в приборе при его эксплуатации в реальных условиях, является одной из важнейших задач, требующих решения при проектировании авиакосмических датчиков, приборов и систем [1]. Условия эксплуатации таких устройств могут быть довольно жесткими. Так, они могут испытывать вибрации с амплитудами до 10 g и с частотами до 2 кГц, ударные нагрузки до 90–100 g, перепады температуры от –50 до +85 ºС, электромагнитные и радиационные воздействия. Помимо этого необходимо принимать во внимание, что датчики и системы, использующиеся в космических аппаратах, могут работать в условиях вакуума и невесомости. При этом тепловые воздействия в подобных условиях могут оказать существенное влияние на эксплуатационные характеристики прибора и, следовательно, на его выходные данные [2–4]. Поэтому необходимо еще на этапе проектирования прибора исследовать возникающие в нем трехмерные неоднородные нестационарные температурные поля с учетом условий его эксплуатации и особенностей его конструкции. При этом особый интерес вызывают именно нестационарные и переходные тепловые процессы.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И АЛГОРИТМ РАСЧЕТА ТЕМПЕРАТУРНЫХ ПОЛЕЙ

Для исследования трехмерных нестационарных температурных полей в различных типах датчи-

ков, приборах и системах на их основе был разработан модифицированный метод тепловых элементарных балансов (МЭБ) [1], который к настоящему времени достаточно хорошо зарекомендовал себя при исследовании температурных полей в различных датчиках и устройствах. Смысл МЭБ заключается в разбиении исследуемого объекта на "элементарные" тепловые объемы, представляющие собой элементы конструкции. В "элементарном" объеме могут находиться источники и стоки тепла. "Элементарные" объемы могут контактировать как между собой, так и с окружающей внешней и внутренней средой, также имеющую температуру. Отличием МЭБ от других методов конечно-элементного моделирования является то, что, во-первых, он сводится к разностной схеме и не требует составлять дифференциальные уравнения, а, во-вторых, рассчитывается средняя температура элементарного объема. При этом приближенное решение, полученное с помощью основного разностного алгоритма МЭБ, сходится к точному решению соответствующей дифференциальной краевой задачи с погрешностью

O ( A t + A x ² + А у ² + A z 2 ).

Математическая модель, выражающая МЭБ, имеет вид [1]:

N

T ⁽ t ^{+ А} t ) = ¹       Z ^Q j ⁺ Qu

_      ci V j = 1

i c

T ( t ) + )_

A t + —

Г N

Z Q j T j ( t ) + Q cT_a (t ) + Q i (t ) , c i V J = 1                                   7

где T (t), T (t + At) — температуры i-го "элементарного" объема (ЭО) в настоящий и последующий момент времени; ci (i = 1, …, M) — теплоемкость ЭО; qij — термопроводимости между i-м и j-м ЭО; qic — термопроводимость между i-м ЭО и окружающей средой; Tсi (t) — температура среды; Qi (t) — мощность источника тепла; M — общее количество ЭО в модели; N — количество ЭО, имеющих тепловой контакт с i-м ЭО; At — шаг расчета.

в

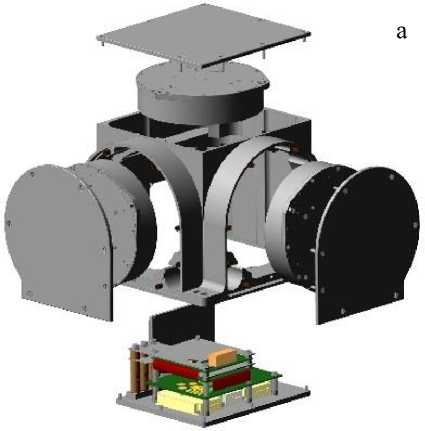
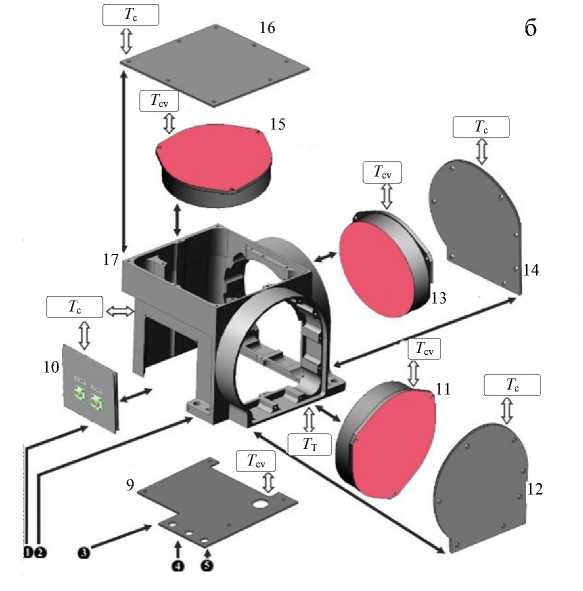
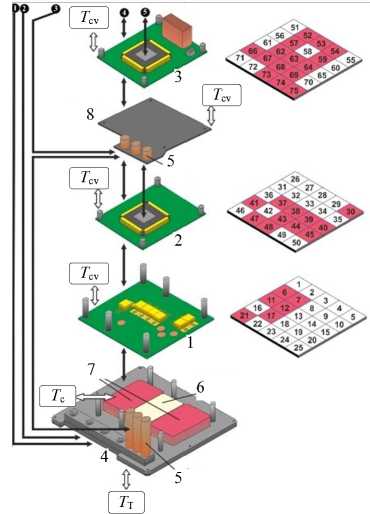
Рис. 1. Компоновка прибора БИУС-М-1 (а) и основные элементы тепловой модели БИУС-М-1 (б, в).

1 — плата 1; 2 — плата 2; 3 — плата 3; 4 — основание; 5 — стойки теплоотвода (низ, верх); 6 — элемент ФПС; 7 — источники питания; 8 — пластина радиатора 1; 9 — пластина радиатора 2; 10 — держатель; 11 — гироскоп 1; 12 — крышка 1; 13 — гироскоп 2; 14 — крышка 2; 15 — гироскоп 3; 16 — крышка 3; 17 — корпус; Т С —температура наружной окружающей среды; Т СV — температура внутренней окружающей среды; Т Т —температура термоплаты

Величина суммарной тепловой проводимости, характеризующаяся входящими в (1) коэффициентами термопроводимости q , может быть представлена в виде q — qТ + qК + qИ — ат fT + акf + aИf ,      (2)

где q _Т , q _К , q _И — коэффициенты термопроводимости, учитывающие теплообмен соответственно теплопроводностью, конвекцией и излучением; α _T , α _K , α _И — функции геометрических и теплофизических параметров ЭО; f _Т , f _К , f _И — функции температур ЭО.

Математическую модель (1) следует дополнить начальными условиями:

T iL — о — t o .     T c L— о — T co .                    (3)

и задача сведется к определению функций T_i ( t ) .

Алгоритм вычисления температурного поля с помощью МЭБ сводится к следующим шагам.

• 1.    Разбиение модели на ЭО. Структура разбиения модели на ЭО представляет собой одну из важнейших проблем при использовании МЭБ. ЭО не обязательно должны быть одного размера, но их величина должна быть достаточно малой, чтобы можно было пренебречь изменением температуры внутри объема.

• 2.    Расчет коэффициентов термопроводимости ЭО между другими ЭО и средой по формуле (2). Расчет этих коэффициентов может представлять определенные трудности, т. к. их значения, вообще говоря, зависят от формы ЭО, площади и формы их контакта между собой и средой, параметров среды, неоднородности материалов конструктивных элементов прибора и т. д.

• 3.    Расчет удельных значений мощностей тепловыделения ЭО.

• 4.    Расчет начальной температуры, согласно начальным условиям (3).

• 5.    Вычисляются значения температур T_i в следующий момент времени по формуле (1).

Математическая модель (1) с условиями (2)–(3) позволяет учитывать многокомпонентность конструктивной схемы прибора, нестационарные источники и стоки тепла в ЭО, тепловое взаимовлияние ЭО, изменение температуры внешней и внутренней окружающей среды по различным законам, в том числе и случайным. К настоящему времени модифицированный метод тепловых элементарных балансов опробован и хорошо себя зарекомендовал при моделировании температурных полей различных приборов и систем, например инерциальных навигационных систем, наноспутников, а также их компонентов.

На основе описанного выше алгоритма были разработаны и зарегистрированы в Федеральном институте промышленной собственности [5, 6] специализированные программные комплексы для моделирования температурных полей в различных приборах и устройствах.

МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНЫХ ПОЛЕЙ В БЛОКЕ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ

Рассмотрим специфику применения МЭБ к исследованию температурных полей в прецизионном приборе на примере блока измерения угловых скоростей БИУС-М-1 на волоконно-оптических гироскопах производства ООО НПП "Антарес", Саратов.

На рис. 1 показана компоновка и тепловая модель прибора [7]. Стрелками на рис. 1, б, в, показаны тепловые связи между элементами БИУС-М-1 друг с другом и окружающей средой.

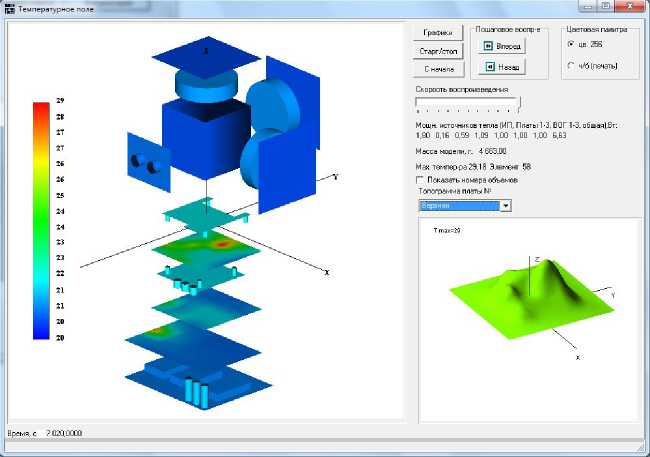
Для расчета температурного поля БИУС-М-1 было создано специализированное программное обеспечение (ПО). В Приложении на рис. П1 представлены диалоговые окна комплекса. Разработанное ПО позволяет в полном объеме управлять параметрами тепловой модели, обрабатывать полученные числовые данные, включая их визуализацию путем построения графиков нестационарных значений температур в расчетных точках, их производных по времени и пространственных топограмм температурных полей плат электроники.

Кроме того, возможно наблюдать динамику изменения конфигурации температурного поля исследуемого прибора в схематически изображенных элементах конструкции, которые в свою очередь возможно копировать в буфер обмена. Возможен также вывод и запоминание в текстовом файле числовых матриц температурных полей с течением времени (протокол расчета).

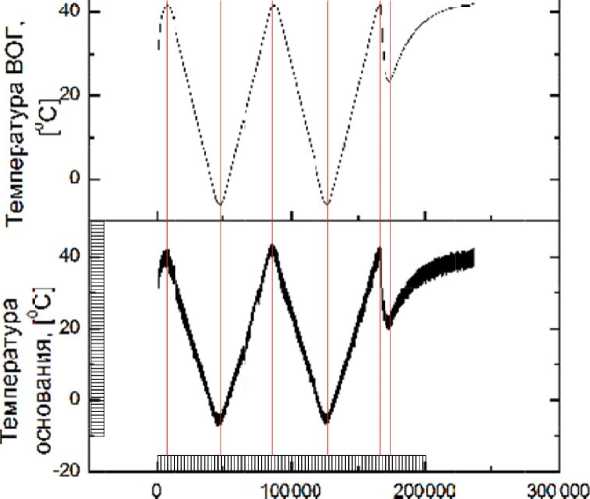
Для проверки адекватности результатов, получаемых в программном комплексе, реализующем математическую модель (1), был проведен ряд экспериментов с БИУС-М-1 в термокамере (рис. 2). На рис. 2, а, приведены данные с термодатчика, установленного на одном из ВОГ при испытаниях БИУС-М-1 в термокамере, на рис. 2, б, результаты моделирования при параметрах, имитирующих такие же условия, что и на испытательном стенде.

Из рис. 2 видно, что экспериментальные данные и данные моделирования с помощью предлагаемого метода практически совпадают, что доказывает адекватность получаемых с помощью МЭБ результатов.

Время, [cj

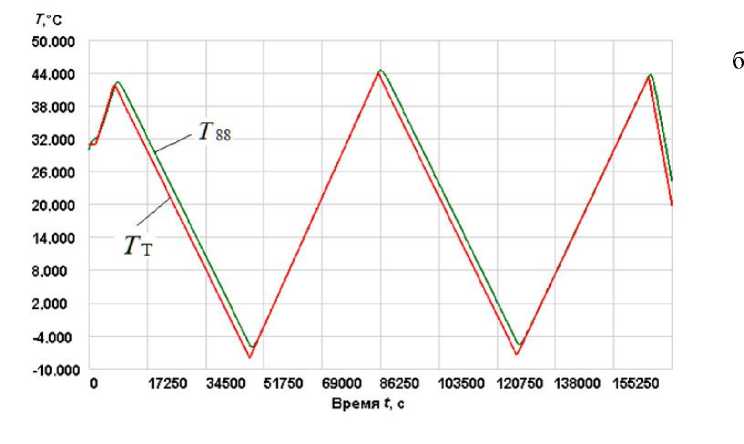
Рис. 2 . Экспериментальные данные (а) и температура термоплаты ( T T ) и ВОГ ( T 88 ) по данным моделирования (б)

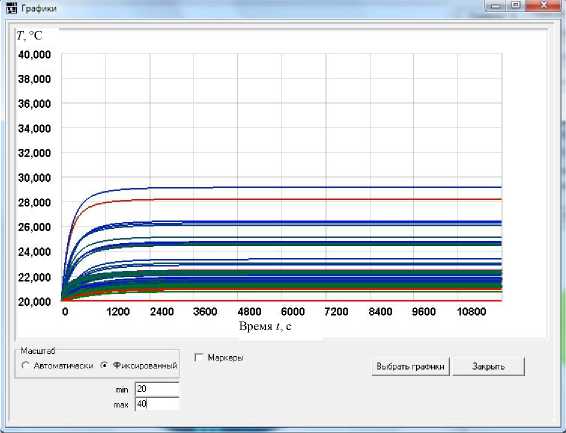
Для исследования температурного поля БИУС-1-М с помощью разработанного ПО проведен ряд компьютерных экспериментов, в которых моделировались различные тепловые режимы в нормальных "земных" условиях и условиях вакуума и невесомости. При этом использовались различные типы возмущающего теплового воздействия: постоянное; гармоническое, имитирующее движение по круговой орбите; по заданной циклограмме; случайное. В Приложении на рис. П2, П3 приве- дены некоторые графики текущих температур в расчетных точках БИУС-1-М, полученные с помощью разработанного ПО.

МЭБ также хорошо себя зарекомендовал при моделировании и исследовании нестационарных температурных полей электронных плат, предназначенных для работы в условиях космического пространства. Например, в электронных платах

а

б

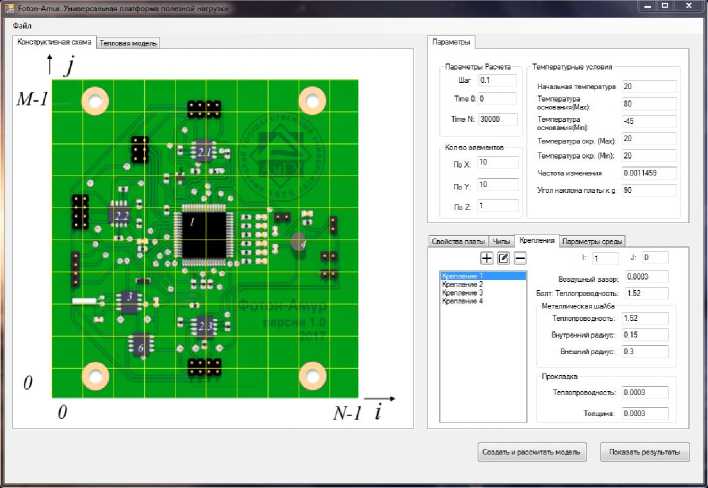
Рис. 3. Моделирование электронных плат наноспутника.

а — общий вид платы модуля полезной нагрузки Фотон-Амур; б — главное окно приложения ФА-Термо 1.0; 1 — корпус наноспутника; 2 — операционный усилитель; 3 — микроконтроллер

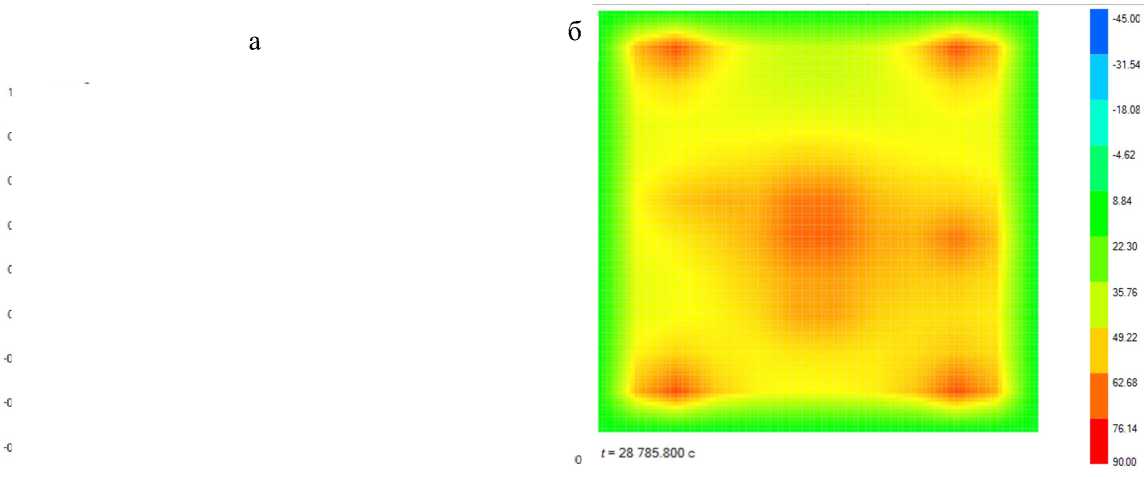
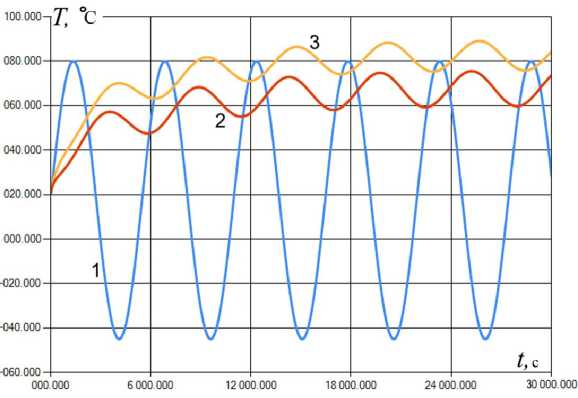
Рис. 4. Графики изменения температуры в элементах модуля полезной нагрузки (а) и его температурное поле в момент времени t = 28785.8 с (б).

1 — корпус наноспутника; 2 — операционный усилитель; 3 — микроконтроллер

наноспутников. На рис. 3 показана электронная плата — модуль полезной нагрузки Фотон-Амур [8] и главное окно программы для моделирования его температурных полей.

Результаты моделирования теплового поля, возникающего на плате при движении спутника по орбите Земли в условиях сильно разреженной атмосферы показаны на рис. 4.

Как видно из рис. 4, температура на электронной плате может достигать 90 ○С при эксплуатации наноспутника в условиях космоса, что может быть небезопасно для его электронных компонен- тов. Поэтому следует еще на этапе компоновки и разработки наноспутника продумать возможность применения пассивных и активных методов снижения тепловой нагрузки на электронные компоненты наноспутника, в том числе применением различных методов термостабилизации.

ЗАКЛЮЧЕНИЕ

На основе проведенных исследований можно сказать, что используемый модифицированный метод элементарных тепловых балансов носит достаточно универсальный характер и может быть использован для исследования трехмерных, неоднородных, нестационарных температурных полей различных типов датчиков, приборов и систем на их основе. Также этот метод применим для исследования многокомпонентных систем, в том числе прецизионных приборов. Использование МЭБ и реализующих его программных комплексов не требует проведения дорогостоящих натурных экспериментов, но при этом позволяет уже на этапе проектирования прибора узнать, насколько он будет подвержен тепловым воздействиям в реальных условиях эксплуатации и при необходимости внести в конструкцию изменения для уменьшения негативного теплового влияния на компоненты и элементы исследуемого устройства или системы.

ПРИЛОЖЕНИЕ

а

б

Рис. П1. Диалоговые окна исходных (а) и выходных данных (б) программного комплекса

б

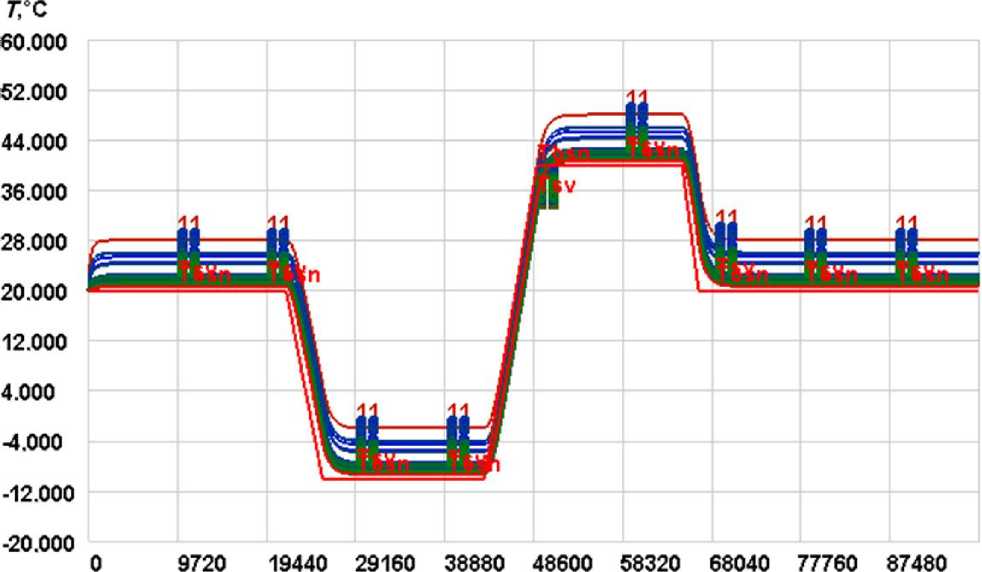
Рис. П2. Текущие температуры T i во всех расчетных точках БИУС-М-1 при температуре среды и термоплаты +40 ^оС при нормальной силе тяжести и нормальном давлении (а) и при невесомости и вакууме (б)

r/c

50 000

44.000

38.000

32.000

26.000

20.000

14.000

8.000

2.000

4.000

-10.000

0      1200   2400   3600   4800   6000   7200   8400   9600   10800

Время t, с

Время t, с

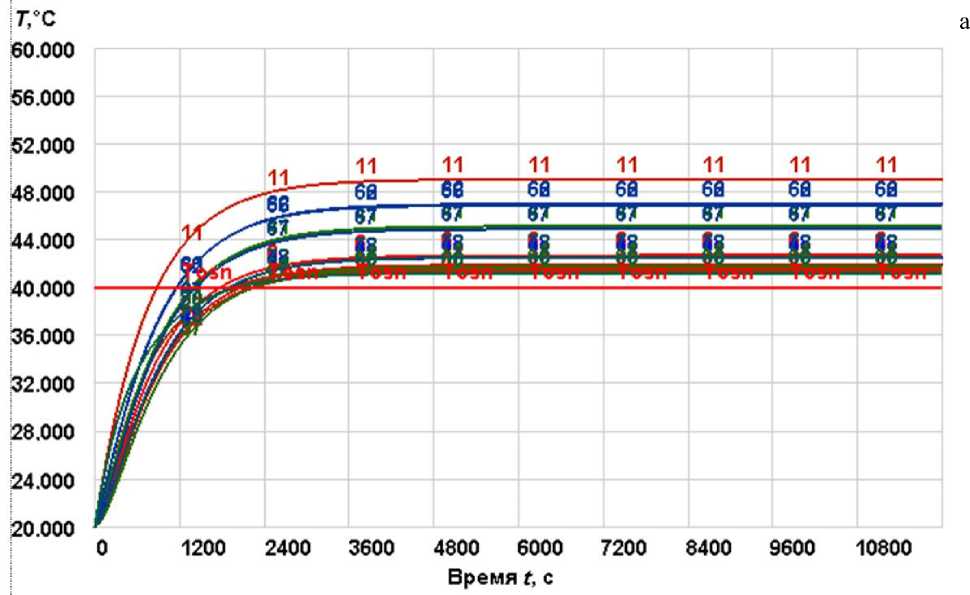
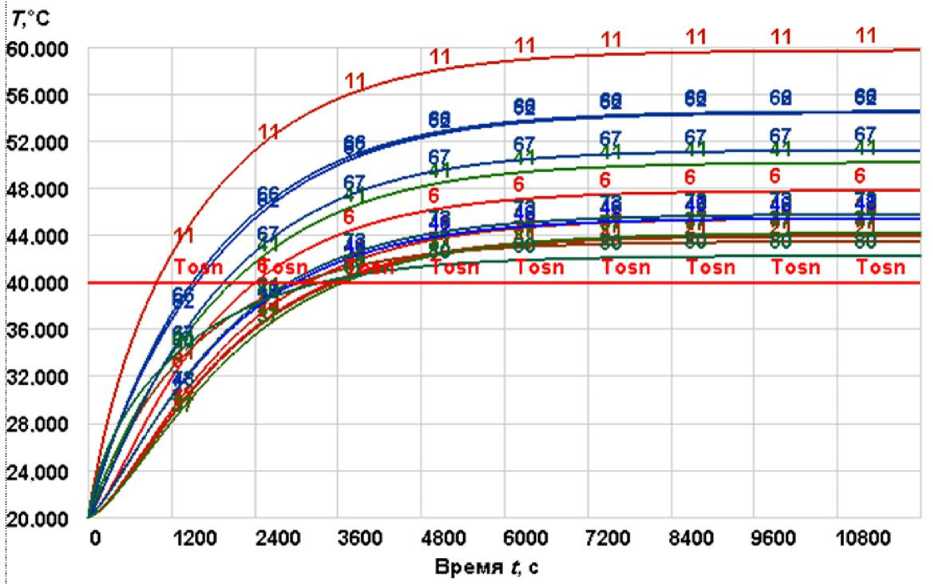
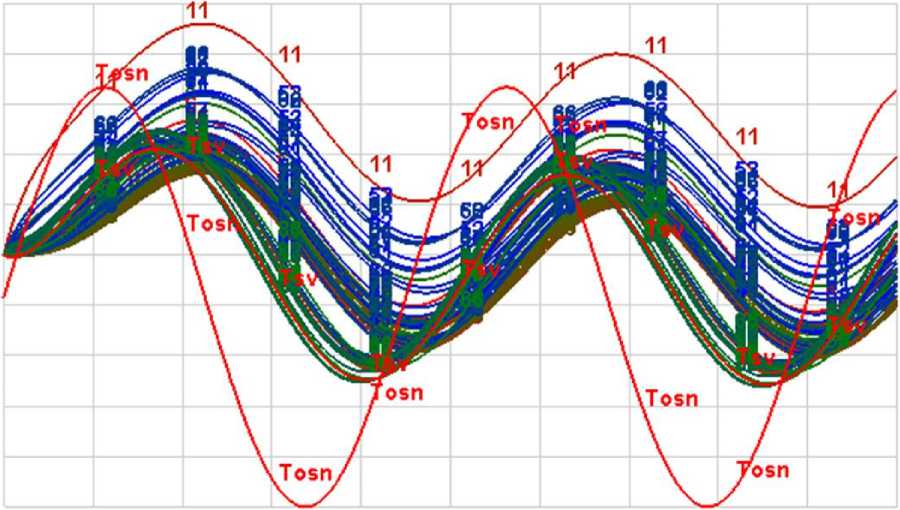
Рис. П3. Текущие температуры T i во всех расчетных точках БИУС-М-1.

а — при гармоническом внешнем температурном возмущении в условиях вакуума и невесомости с периодом 90 мин; б — по заданному термоциклу