Алгоритмы метода усреднения координат при поиске главных минимумов многоэкстремальных функций

При решении проблемы многокритериальной оптимизации часто основываются на одном из показателей эффективности и минимизируют (или максимизируют) его, а остальные показатели выдерживают не хуже заданных (так появляются дополнительные ограничения неравенства). В ограничения неравенства входят также ресурсные и конструктивные ограничения. При такой оптимизации исследователя интересу- ет не только положение глобального минимума выбранного показателя эффективности, но и положение близлежащих (по величине минимизируемой функции) минимумов. Указанные минимумы назовем главными.

В работе [1] предложен алгоритм поиска главных минимумов без ограничений неравенств, в [2, с. 139–143] были проведены испытания алгоритма на простейших численных. В работе [3] предложено три эвристических способа учета ограничений, основанных на последовательном выборе наилучшей точки в области поиска и выделении окрестности вокруг нее.

В предлагаемой работе рассматривается еще один способ выделения подобластей, соответствующих главным минимумам, путем многократного запуска алгоритмов, основанных на методе усреднения координат, по всей области поиска с исключением найденных областей с помощью добавления дополнительных ограничений неравенств.

Постановка задачи. Необходимо найти заданное количество главных минимумов функции многих переменных:

I ( x ) = гл мин, x = ( x 1 ,..., X m ) T . (1) x е X

Допустимая область X определяется системой ограничений неравенств фу(x) ^ 0, j = 1, m1 • (2)

Минимизируемая функция качества I ( x ) имеет широкий диапазон свойств. Она может быть многоэкстремальной, разрывной, недифференцируемой, искажена помехой. Ограничения (2) сужают область поиска экстремума. Функции ограничений ф j ( x ), j = 1, m₁ также могут быть невыпуклыми и недифференцируемыми. Допустимая область может иметь вид «узкого жгута». Поиск минимумов осуществляется только на основе измерений или вычислений указанных функций: I ( x ); ф j ( x ), j = 1, m₁ .

Алгоритмы. Три представленных ниже алгоритма включают в себя два этапа: первый этап – это разбиение исходной области на подобласти, второй – поиск глобального минимума в каждой из найденных подобластей. Особенность предлагаемых алгоритмов заключается в том, что на первом и втором этапе используются одни и те же алгоритмы усреднения координат, но запускаемые в разных областях и с разными наборами ограничений. Учет ограничений производится так же, как и в работе [3].

Исследователь задает:

• -    исходную гиперпрямоугольную область П ⁰ (с центром e x ⁰ и интервалами A x ⁰), которая должна содержать в себе искомые главные экстремумы;

• –    количество исходных пробных точек n ⁰ , равномерно распределенных внутри области П ⁰;

• –    количество искомых главных минимумов n _глмин ;

  – количество пробных точек n , вид ядра и степень s его селективности, используемых при поиске глобального минимума в каждой подобласти.

Первый алгоритм (с использованием пробных точек внутри допустимой области).

В заданной прямоугольной области поиска П ⁰ последовательно равномерно размещаются пробные точки, и из них формируется n ⁰ точек, попадающих в допустимую область (2). Разбиение пробных точек

x(1), i = 1, n0 на группы точек, тяготеющих к главным минимумам, производится следующим образом. В пробных точках вычисляется функция качества I(x(1)) = I(1), i = 1, n0 , и на основе алгоритма глобальной оптимизации (описанного ниже) в области П1 = П0 х X отыскивается такая точка xмин, которая соответствует наименьшей величине исходной функции качества I= мин I(x). Затем вокруг этой x е{П0 х X} точки выделяется подобласть некоторого размера, например Ax0 / c, v = 1, m . Обозначим эту подобласть как П0р и добавим ее к списку ограничений (2), тем самым исключив ее из области П0. Далее, аналогичным способом, ведется поиск в области П2 = П1 \ П0р и получается область Ппр с центром в xмин и т. д. Выделение подобластей осуществляем до тех пор, пока их количество не станет равным заданному количеству nглмин главных минимумов или алгоритм не сможет выполнить поиск xмин для очередной подобласти.

Параметр c >  1 определяет размеры подобластей и задается исследователем пока интуитивно на основе размеров исходной области П ⁰ , априорной информации о функции качества и требуемого количества главных минимумов n _глмин .

На этом первый этап – разбиение исходной области на подобласти – считается завершенным.

На втором этапе производится отыскание экстремумов в каждой найденной подобласти. При этом к неравенствам (2), которые входят в исходную постановку задачи, добавляются неравенства, определяющие прямоугольные подобласти, найденные на этапе разбиения исходной области на подобласти. Добавление таких неравенств не дает алгоритму выходить за границы этих подобластей и исключает многократные попадания в один и тот же экстремум.

Опишем алгоритм движения к минимуму на ( l + 1)-м шаге, если на предыдущем шаге был получен вектор искомых переменных x^l :

n хl+1 = xl + /Хх1 и ; и     = У и)i)р(i) , v = 1, т;

V     ^V   '-^v ^нУ,мин ^; ^V,MИH / 1 v p s ,мин ,        ,   ^;

i =1

( i ) p s , мин

p ( g ^{( i )} ) s мин

n ;

( j )

s gмин j=1

( i ) g мин

_I ( i )

I мин

I макс

I мин

Л n                Л ^{1 q} _____

Ахl+1 = у -Axl  VAi) |qp(i)      _ v = Lm *

v Y q ^Vv I / v I v   I ps,мин I ,          ,,

V i=1

l = 0, 1, 2, - ;

x ^{0 =} x п ⁰ одобл , ^{A x 0 = A x} п ⁰ одобл ; ^[0 < Y q , 4 ^ ^{{1, 2} ^ }, ⁰ <  ^{S ]},

где I мин = ^мин{ I ⁽ⁱ\ i = 1, n ^}, I макс = ^макс{ I ^<0, i = 1, n ^}; Y _q - коэффициент растяжения области варьирования; s - коэффициент селективности ядра p s ( ■ ); в пере-

менных u V i ) , p S М _ин, I⁽ i ) для упрощения записи опущен номер итерации l ; всегда 0 <  g мин <  1. Ядра p _s ⁽ _, ⁱ _м⁾_ин нормированы на системе n пробных точек:

Ф _у -,мин = ^мин{ Ф _у ⁽ x ^Х i ^: 0 < Ф ⁽ x ^{( i ))}} , Ф у -макс = ^MаКс{ Ф j ⁽ x^Ч i ^:0 < Ф _У ⁽ x ^{(0 )}} .

Если при некотором j = l множество

n

p(i) s,мин i=1

= 1.

Перед совершением ( l + 1) -го рабочего шага для

получения пробных точек x ⁽ i ) , i = 1, n , последовательно генерируются точки (равномерно распределенные) в прямоугольной области A x¹ с центром в точке x^l :

{ i :0 <ф l ( x ⁽ i ) )} пустое, то этот номер l не входит во множество J ^{( i )} (для каждого фиксированного i ). Для пробных точек, в которых ни одно неравенство не нарушено (т. е. множество J ^{( i )} пустое) штрафная добавка берется равной нулю.

Если при некотором j = l множество

x V i ) = x V + A x V ■ u V i ) , u V e [ - 1; 1], v = 1, m , i = 1, 2,

Из них оставляется n точек, попадающих в допустимую область, задаваемую ограничениями (2): ^x ° = ^x м ин , ^{A x} ° = ^П пр , ^j = ¹ n глмин . В пробных точках вычисляется минимизируемая функция I ⁽ i ) , i = 1, n , и на основе этих экспериментальных данных [ x V i ) , V = 1, m , I ⁽ i ) , i = 1, n ] совершается вышеприведенное рабочее движение и пересчитываются размеры области поиска.

Критерием останова процесса поиска обычно служит условие уменьшение размера области варьирования A x l до заданной величины: max{| A x V |, v = 1, m } < e .

Значения p_s ( g ) на интервале изменения 0 <  g <  1 являются неотрицательными, убывающими ядрами. Выбор формы и коэффициента s селективности ядра существенно влияет на характеристики поиска глобального минимума. Чаще всего используется степенное ядро p_s ( g ) = (1 - g^r ) ^s , r = 1,2,3,.... Коэффициент s для степенных ядер лежит в широком диапазоне целых положительных чисел и подбирается сравнительно просто.

Второй алгоритм (с переходом к штрафной функции).

Введем вместо функции качества (1) и ограничений (2) штрафную функцию:

{i :0 <ф l ( x ⁽ i ) )} состоит из одного элемента, то соответствующий элемент в функции (4), входящий под оператор max{} , полагаем равным 1: ^[ Ф l ⁽ x^{(i )) -}ф l ,м _ИН^]/^[ Ф l ,ма _К с ^-Ф l ,„, ] =1-

Далее, разбиение на подобласти происходит как для первого алгоритма, но пробные точки размещаются равномерно по всей подобласти П ⁰ (а не в ее части, как в предыдущем алгоритме) и вместо исходной функции I ⁽¹) и ограничений ф j ( x ⁽ i ) ) используется штрафная функция I ^{( i )} (4).

После разбиения П ⁰ на подобласти, поиск условного глобального минимума в каждой из подобластей (второй этап) ведется так же, как и в первом алгоритме, но пробные точки размещаются равномерно в каждой подобласти П пп _р, j = 1, n _глмин без учета ограничений (2) и вместо исходной функции I ^{( i )} используется штрафная функция I ^{( i )} (4).

Третий алгоритм (с переходом к многомерным ядрам).

Будем учитывать ограничения путем расширения вида нормированные ядра p _s ^{( i )} :

Р 1, s ⁽ g ^{( i ))} П Р 2, S ⁽ g j) )

P ^i) =  -------------------------,          (5)

£ P 1, S ⁽ g ^<Ю) П P 2, S ⁽ g Г)

P=1                 j e J > " >

.      I

I макс   I мин

g j ) =

Ф у ⁽ x ^{<0) -}Ф _У ,мин    .   1-----

—----—, j = 1, m 1 ;

^ф j ,макс ^ф j ,мин

+a ■ max

( i )

I( x (i)) = I макс

I мин

I мин

+

p _{1, s} – ядро по оптимизируемой функции; p _{2, s} – ядро

Ф ⁽ x ^<0) -Ф^ мин ^ф j ,макс ^ф j , мин

j e J ^{( i )} e 1, m ^ ,

по ограничениям.

Значения I макс , I мин , ф _{у >а}кс , ф _у _мин для каждого фиксированного j , а также множество J ^{( i )} вычисля-

ются так же, как и для второго алгоритма.

i = 1, n ⁰, a >  0 .                     (4)

Если при некотором j = l множество J ⁽ i ) состоит

Здесь множество J ^{( i )} включает только номера тех функций ограничений, для которых ограничения нарушены: при j e J ⁽ i ) e 1, m ₁ всегда 0 <ф j ( x ⁽ i ) ); I мин = ^мин{ I ^<0 > i = ¹ n ^}, I макс = ^макс{ I■ i = ¹ n ^}; для каждого фиксированного j :

из одного элемента, то аргумент ядра p _{2, s} полагаем равным 0,75. Это значение было получено экспертным путем. Если во всех пробных точках неравенства (2) не нарушены, то ядра становятся одномерными и зависят только от оптимизируемой функции:

^{Р (}‘⁾ = P 1S ⁽ g ⁽ⁱ⁾⁾/ ILp^, S ⁽ g ^<Ю) .

/ p=1

Таким образом, базовый алгоритм (3) трансформируется следующим образом:

^{1 + 1}                      lu                                    (i) ¹ )"n(¹ )

x V     x V ⁺ ^ x V u V,MИH , u V,MИH У u v p s ,мин , ^V 1, m ;

i =1

P 1, s ( g MИн ) П P 2, s ⁽ g j) )

p (i)  =J• ps, мин

У Pi,,(g мин) П p 2, s(gjM')

=1                 j e J(^)

I ( i ) - Г

• ( i )мин

g мин макс мин

/ n              V/ q ____

Ax1+1 = у • kxl УI (i)1) q p( 1)       , v =,

V Y q v I v      ps,мин I ,           ,,

V i=1

l = 0, 1, 2,_;     0 _q ; q e {1, 2, -}; 0 <  s .

Разбиение на подобласти производится так же, как в первом алгоритме, но пробные точки равномерно размещаются по всей области П ⁰, а точки x мм _ин отыскиваются на основе алгоритма (6).

После разбиения П ⁰ на подобласти поиск минимума в каждой из подобластей ведется также, как и в первом алгоритме, но пробные точки размещаются равномерно в каждой подобласти П пп _р, j = 1, n _глмин без учета ограничений (2), и поиск условного глобального минимума в каждой подобласти производится на основе алгоритма (6).

Численный пример. Исследуем поведение алгоритмов при наличии аддитивной помехи и допустимой области в виде «узкого жгута». Как и в работе [2, с. 93], в качестве помехи будем использовать аддитивную равномерно распределенную помеху R [ —6 ; 6 ] = 6¹ R [ — 1; 1], принадлежащую интервалу [ -0 ; 6 ] (здесь 6 определяет уровень помехи). Выбор равномерного закона распределения помехи соответствует наихудшей ситуации, которая, в принципе, может встретиться при реальном искажении оптимизируемой функции. При этом помеха имеет максимальную приведенную энтропию среди всех непрерывных случайных величин (с любым законом распределения), изменяющихся внутри конечного интервала [ -6 ; 6 ]. Рассмотрим четырехэкстремальную потенциальную функцию, построенную за счет применения операции min к четырем элементарным экспоненциальным потенциалам:

I ( x ) = min { - 3 exp { - 3[| x 1 - 3 |^1,5 + | x ₂ |^1,5]}, - 5exp{ - 2,5[| x 1 + 3| 2,5 + | x ₂ |² , ⁵]}, - 7exp{ - [| X 1 f, ² + | x 2 - 3|^1,2]},

• -10exp{-2[|x1|2 +|x 2 + 3|2]}}.(7)

Допустимая область имеет вид кольца шириной А :

x2 + x22 < (3 + А)2 и x2 + x22 > (3 -А)2.(8)

12   2   12

Пространственный вид функции (7) представлен на рис. 1. Она имеет минимумы в точках (–3; 0), (3; 0),

(0; 3), (0; –3) и принимает в них, соответственно, значения (–3), (–5), (–7), (–10). Линии равных уровней функции (7) и допустимая область (8) при А = 0,4 приведены на рис. 2. Соответственно, задавая 6 = 5, мы получим 100 % помеху.

Все три вышеописанные алгоритма хорошо справляются с поиском условного глобального экстремума при отсутствии помехи и достаточно узкой допустимой области А = 0,01.

Изменение по итерациям минимизируемой функции при поиске двух главных минимумов функции (7) при ограничениях (8) и А = 0,01 для всех трех алгоритмов отражено на рис. 3.

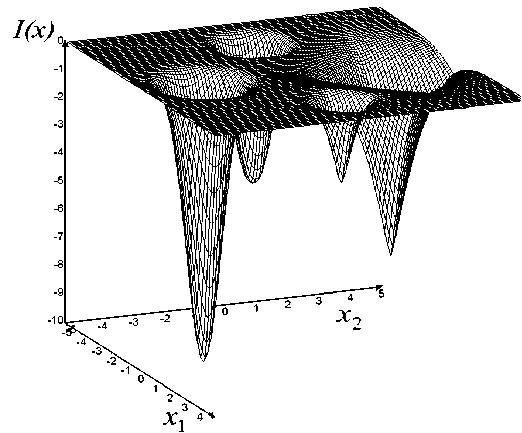
Рис. 1. Потенциальная функция (7)

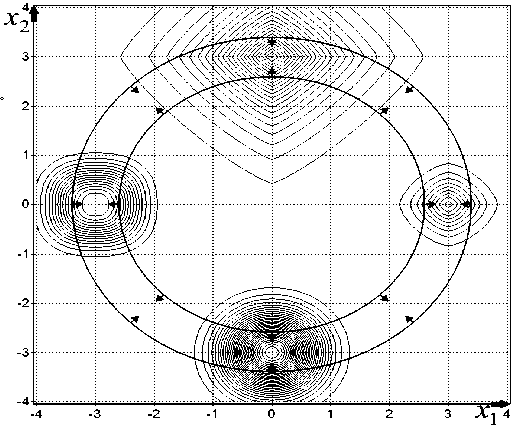
Рис. 2. Равные уровни функции (7) и допустимая область (8) при А = 0,4

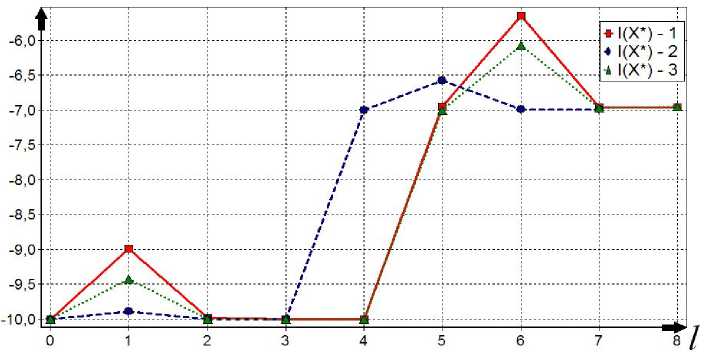
Рис. 3. Процесс поиска двух главных минимумов всеми алгоритмами

Все алгоритмы ведут себя примерно одинаково и отыскивают два главных минимума за 7–8 итераций

(рис. 3). Начальная точка поиска находится в малой окрестности истинного решения и алгоритмы ее лишь уточняют, это обусловлено тем, что еще на первом этапе (выделение подобластей) происходит достаточно точная оценка положения главных минимумов.

Проведем исследование поведения алгоритмов при наличии узкой допустимой области ( Δ = 0,01 ) и различных уровнях помехи. Для этого будем менять уровень помехи θ от 0 до 5 (от 0 до 100 % помехи) с шагом 1 и усреднять полученные значения на каждом шаге по 101 запуску. В качестве меры качества работы алгоритмов будем использовать количество попыток размещения пробных точек N и оценки вероятности отыскания «истинных» главных экстремумов _P ˆ( x ^* - x ≤ ε ) .

Первый алгоритм. Считаем, что n ⁰ = 500, область поиска с центром x ⁰ = (0; 0) и размером Δ x ⁰ = (4; 4), q = 2 , γ _q = 1,2 , ядро по функции качества – параболическое с коэффициентом селективности s = 300 , размер выборки при поиске экстремума в подобласти n = 250. Графики, показывающие оценки вероятности отыскания истинного экстремума и количество пробных точек при разных уровнях помехи, представлены на рис. 4.

Первый алгоритм отыскивает оба экстремума практически с вероятностью 1, но при этом алгоритм размещает очень большое число пробных точек: 1,3∙106 (рис. 4). Такое поведение обусловлено структурой ограничений – узкая область в виде жгута не дает алгоритму размещать точки нигде, кроме как в этой области. Таким образом, алгоритм практически гарантированно отыскивает заданные экстремумы, даже при 100 % помехе (если ограничений станет еще больше, то алгоритм вообще не сможет разместить пробные точки за разумное время).

Второй алгоритм . Зададим такие же параметры, как и для первого алгоритма. Штрафной коэффициент α = 1,1. Графики, описывающие поведение алгоритма при различных уровнях помехи, представлены на рис. 5.

Второй алгоритм размещает гораздо меньше пробных точек (в 40 раз), чем первый алгоритм (рис. 5). Вероятности отыскания главных минимумов хуже, чем у первого алгоритма, но вполне неплохие при таких уровнях помехи. Этот алгоритм эффективен и прост в настройке.

Третий алгоритм . Зададим такие же параметры алгоритма как и для первого алгоритма. Ядро по функции качества – степенное гиперболическое [2, с. 67] степень ядра r = 2 , коэффициент селективности s = 600, ядро по ограничениям – параболическое с коэффициентом селективности s = 100. Графики, описывающие поведение алгоритма представлены на рис. 6.

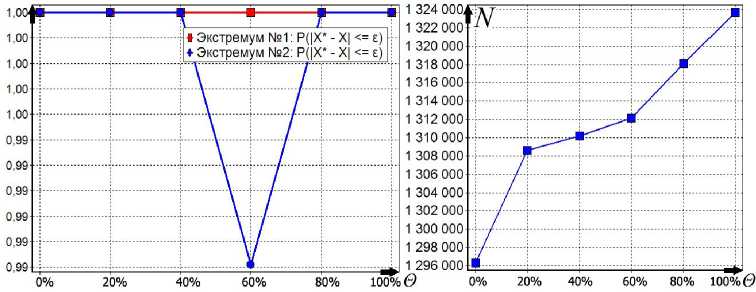
Рис. 4. Зависимость показателей качества работы первого алгоритма от θ

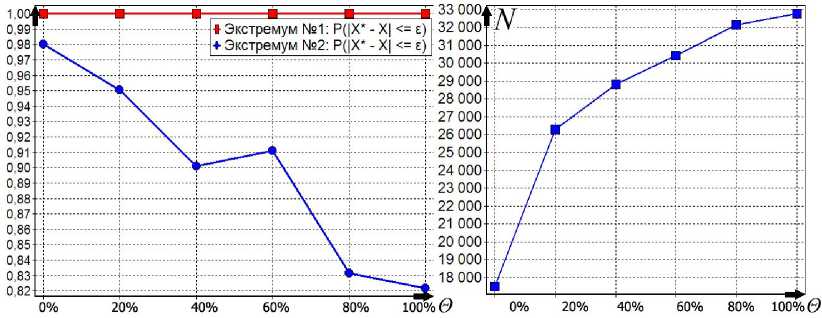
Рис. 5. Зависимость показателей качества работы второго алгоритма от θ

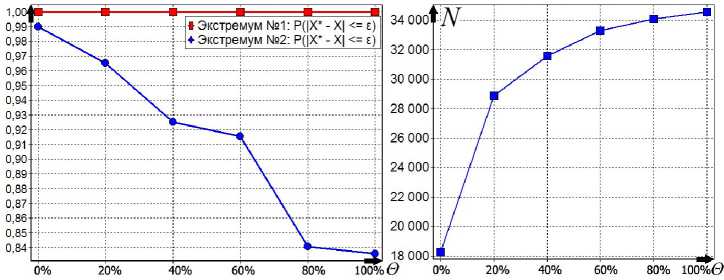
Рис. 6. Зависимость показателей качества работы третьего алгоритма от θ

Третий алгоритм работает чуть лучше, чем второй алгоритм (рис. 6), но он гораздо более сложен в настройке, так как необходимо настраивать два ядра вместо одного (пришлось настраивать не только степень и селективность ядра, но и его вид).

Качество работы второго и третьего алгоритма можно еще повысить, задав n ⁰ = 1 000 и n = 500, но это приведет к увеличению количества пробных точек.

Программная реализация алгоритмов. Представленные алгоритмы входят в состав пакета глобальной оптимизации Global Optimizer v 2,0, в котором также представлены основные алгоритмы глобальной оптимизации, базирующиеся на методе усреднения координат. Пакет реализован на языке Delphi с использованием среды визуального программирования Delphi 2010 фирмы Embarcadero Technologies и функционирует в операционной системе из семейства Windows 2 000/XP/Vista/7.

При проектировании программных алгоритмов поиска главных минимумов был использован объектно-ориентированный подход. Алгоритмы реализованы как надстройка над алгоритмами поиска глобального экстремума [2]. Этот подход позволяет распараллелить поиск главных экстремумов и тем самым значительно повысить скорость работы алгоритма. Этот вариант требует специальных исследований.

Алгоритмы поиска главных экстремумов привлекают своей простотой, сравнительно небольшими вычислительными затратами, высокими точностными показателями. Проведенные исследования показали, что все три алгоритма примерно одинаково эффективны при наличии сильной помехи. Наилучшие показатели оказались у второго и третьего алгоритмов – они отыскивают главные минимумы с достаточно высокой вероятностью и при этом размещают разумное число пробных точек.