Алгоритмы обучения нейронных сетей распознаванию изображений по равномерному критерию

Слоистые нейронные сети прямого распространения используются во многих предметных областях [1, 2] благодаря способности обучения и обобщения исходных данных. Большую роль в этом играет существование эффективных алгоритмов обучения, наиболее известным из которых является алгоритм обратного распространения ошибки, основанный на градиентном методе поиска экстремума и использующий свойство нейронных сетей быстро вычислять производные по своим параметрам [1, 2].

Постоянно растущая сложность прикладных задач, нелинейное увеличение объемов данных и их размерности оставляют актуальной задачу повышения эффективности алгоритмов, используемых для обучения нейронных сетей. При практическом использовании последних неизбежно возникает вопрос выбора структуры сети. Основной задачей становится не просто обучение, а нахождение нейронной сети, наилучшим (в некотором смысле) образом решающей поставленную прикладную задачу. Существует ряд методов нахождения такой сети, основанных на эмпирическом исследовании [2, 3]. Использование этих методов в основном предполагает, что обучение является операцией в решении задачи оптимизации структуры сети. В таком случае потребность в быстром обучении еще больше возрастает.

В данной работе рассматриваются некоторые модификации обучения нейронной сети по алгоритму обратного распространения ошибки для гарантированного распознавания обучающих примеров - в соответствии с равномерным критерием качества обучения. Сеть используется для распознавания изображений цифр.

Проблемы обучения нейронной сети с использованием среднеквадратического критерия

Нейронная сеть используется для решения задачи распознавания образов, в частности для распознавания изображений цифр. Важной особенностью является факт, что все векторы признаков, составленные по изображениям цифр, однозначно относятся к какому-либо, и только одному, классу. Следовательно, можно считать, что существует решение задачи разделения классов в пространстве признаков с нулевой вероятностью ошибки.

В большинстве случаев при обучении нейронных сетей прямого распространения с сигмоидальными активационными функциями для оценки качества классификации используется величина [1, 2, 3]

H s = ¹ z ( y⁽ ,N ’ - d i,q ) ². (1) ² i , q

Здесь y N ) - реальный выход i -го нейрона выходного слоя N нейронной сети при подаче на ее входы q -го образа; d i , _q - желаемое выходное состояние этого нейрона. Суммирование ведется по всем нейронам выходного слоя и по всем обучающим примерам. Обучение нейронной сети при этом сводится к минимизации (1). Однако для описания качества работы нейронной сети при эксплуатации ее в рабочем режиме обычно используют оценку вероятности правильного или ошибочного распознавания образов, которые в общем случае в обучении прямого участия не принимали. При этом оценка вероятности на процесс обучения никакого воздействия не оказывает.

Таким образом, для настройки нейронной сети минимизируется функция, которая не характеризует напрямую качество ее работы. Более того, во время обучения все образы, подаваемые на вход нейронной сети, вносят неравноправный вклад из-за различных величин отклонений желаемых выходов нейронов от реальных. В случае малого количества обучающих примеров это дает положительный эффект, т.к. сеть ориентируется на обучение образов, дающих максимальное отклонение. При большом количестве обучающих примеров их неравноправность во время обучения может привести к негативным последствиям. В частности, нейронная сеть может научиться распознавать большое количество образов с малой ошибкой, при этом некоторые образы будут распознаваться неправильно. Тем не менее, такая ситуация при ее оценке по критерию (1) будет лучше, нежели правильное распознавание всех образов с большей величиной отклонения выходов нейронов от желаемых. Кроме того, обучение по критерию (1) не гарантирует, что будут правильно распознаваться все примеры даже из обучающего набора данных.

Существует несколько способов преодоления указанного недостатка обучения: использование контрольной выборки, упрощение структуры нейронной сети, разбиение обучающих примеров на группы с обучением отдельных нейронных сетей на каждой группе [2, 3]. Эти методы требуют неоднократного проведения процесса обучения с выбором лучшего варианта. В настоящей работе исследуются алгоритмы обучения безошибочного распознавания всех примеров.

Равномерный критерий качества обучения

Будем использовать в качестве активационной ограниченную нечетную возрастающую функцию, например, f (5) =---

1 + exp - a ⁵   2

.

Введем понятие допустимости ответа нейронной сети на заданный входной вектор x , относящийся к классу k . Будем считать, что нейронная сеть выдает допустимый выходной вектор (допустимый ответ) y =( y ₁,…, y _l), если выполняется условие:

Ук ^ cv , У U к < - c v

где c v – порог допустимости: величина из области значений функции активации нейронов выходного слоя.

Будем интерпретировать ответ нейронной сети по правилу «победитель забирает все»: номер нейрона, выдавшего максимальный сигнал, является номером распознанного класса. Тогда условие правильного распознавания принимает вид:

Ук >  У » к . ⁽⁴⁾

Несложно показать, что справедливы следующие свойства:

Свойство 1 . Если ответ является допустимым при c v >0, то он является правильным.

Свойство 2 . Для каждого правильного ответа существует такой порог c v , при котором он является допустимым.

Свойство 3 . Если ответ является допустимым при некотором пороге c v , то он является допустимым и при меньшем пороге допустимости.

Согласно свойству 3 можно найти порог, при котором ответы по всем обучающим примерам являются допустимыми:

c„ = min max c ⁽ q\                            (5)

vv q cv(q )

( q )

где c _v – порог допустимости для q- го обучающего примера. Тогда при использовании активационной функции (2) оценка ошибки (1) по всем обучающим примерам примет вид:

E <  2 QM ^ c v - 2^ J ,                      (6)

где Q – количество обучающих примеров, M – число классов (нейронов в выходном слое).

Так как в нашем случае имеют смысл c v <1/2, оценка (6) убывает с ростом c v . С учетом свойства 1

допустимости ответа нейронной сети процесс обучения нейронной сети как минимизацию ошибки (1) можно заменить максимизацией порога c v . При этом достижение условия c v >0 вместе со снижением ошибки нейронной сети H S будет означать правильность распознавания всех примеров из обучающей выборки.

Алгоритм поэтапного обучения

Обучение нейронной сети с использованием критерия (5) состоит в выборе некоторого порога допустимости нейронов c v и настройке параметров нейронной сети до выполнения условия (3) для каждого обучающего примера. При выполнении этого условия для выхода нейрона ошибку y i• , q - d i• , q можно считать равной нулю. Если в процессе обучения ошибка всех нейронов становится нулевой, то считаем, что сеть научилась должным образом реагировать на этот обучающий пример, и он не участвует в вычислении корректировок параметров сети. В результате такого отбора сокращается количество модификаций параметров нейронной сети. При активационной функции (2) выбор c _v = -0,5 и обучение сети до выполнения условия (4) приведет к настройке сети распознавать образы по правилу «победитель забирает все». Большие значения порога накладывают дополнительные ограничения на выходы нейронов. Подробнее эксперименты с обучением нейронной сети c целью сделать допустимыми все обучающие примеры при заданном пороге c v , описаны в работе [4].

В настоящей работе исследуется возможность еще более эффективного использования отбора обучающих примеров путем внесения небольших изменений в алгоритм обучения.

Исходный алгоритм обучения [4], который далее будет называться выборочным, выглядит следующим образом:

задать порог выходов нейронов c v цикл : пока есть недопустимые ответы цикл : для всех обучающих примеров если ответ недопустим то скорректировать параметры сети

Модификация выборочного алгоритма состоит в итерационном обучении сети с постепенным увеличением порога допустимости от минимального до заданного значения. Такое изменение алгоритма выражается введением дополнительного внешнего цикла:

задать минимальное значение c доп .

цикл : до c доп >= c v цикл : пока есть недопустимые ответы цикл : для всех обучающих примеров если ответ недопустим то скорректировать параметры сети увеличить с доп .

Если на начальном этапе задать сдоп > cv, то обучение будет происходить как в выборочном алгоритме. В противном случае тело внешнего цикла будет дополнительно выполнено некоторое количе- ство раз, в зависимости от закона изменения cдоп. Будем использовать такой закон изменения, для которого цикл заканчивается при сдоп = сv. Тогда коли- чество дополнительных итераций может являться характеристикой измененного алгоритма. В данной работе используется изменение порога допустимо- сти выходов нейронов по закону

_c ( k ) c доп

с max

(0) k

\y max    ^c доп ) ^a ’

где k – номер итерации, cдоп – начальное значение cдоп , ymax – максимальное значение активационной функции нейронов; коэффициент α<1 определяется из условия сДK = cv, K - количество дополнительных итераций. Назовем обучение по этому алгоритму поэтапным с количеством этапов K.

Второе исследуемое изменение алгоритма обучения состоит в применении техники пакетного обучения. Она заключается в том, что модификация вектора параметров нейронной сети W нов = W +Δ W происходит не сразу после нахождения недопустимого примера, а после накопления корректирующего вектора Δ W на определенном количестве обучающих примеров A W= ^ A W q . Суммирование ведется по тем примерам, по которым происходит обучение, т.е. для которых нейронная сеть выдает недопустимый ответ.

По мере обучения нейронной сети количество недопустимых ответов в течение одной эпохи уменьшается. Когда все примеры будут обрабатываться корректно, обучение останавливается. Так как заранее нельзя предсказать количество ошибок для текущей эпохи, то накопление Δ W должно происходить до тех пор, пока либо количество примеров не превысит заданный предел L , либо не закончится эпоха обучения. Величина L представляет собой максимальный размер пакета с ошибочно распознаваемыми обучающими примерами, в рамках которого происходит расчет корректирующего вектора Δ W перед модификацией параметров нейронной сети W . Алгоритм с накоплением корректировок вектора параметров нейронной сети перед его изменением можно записать следующим образом:

задать порог допустимости cv цикл: пока есть недопустимые ответы

{ цикл: для всех обучающих примеров если ответ недопустим то если счетчик_НК=L

{ скорректировать параметры сети обнулить счетчик_НК

} иначе увеличить счетчик_НК если счетчик_НК>0

скорректировать параметры сети

}

Счетчик_НК означает количество неучтенных (накопленных) корректировок сети – текущий размер пакета.

Обучение на худших примерах

Поэтапное обучение заключается во введении допусков на значения выходов нейронов последнего слоя сети c v и - c v . Если выход нейрона, соответствующего классу образа, превышает порог для нейрона с максимальным выходом c _v, а значения выходов всех остальных меньше порога - c _v, то считается, что образ распознается правильно, и коррекция параметров нейронной сети не производится. Значения порогов меняются по мере обучения, приближаясь к желаемым уровням. Обучение сети при фиксированных порогах является одним этапом обучения. Зависимость характеристик поэтапного обучения от количества дополнительных этапов (см. раздел с результатами экспериментов) позволяет предположить о существовании закономерности между количеством этапов и временем обучения, а также числом корректировок параметров нейронной сети. Параметр, определяющий алгоритм – количество этапов K – может неограниченно возрастать. Количество корректировок при возрастании числа этапов линейно снижается (начиная с 4-х этапов), однако эта тенденция ограничивается положительным значением: при обучении параметры нейронной сети должны быть скорректированы хотя бы один раз.

Характер зависимостей при значениях K, близких к тысяче, остается неизменным, а дальнейшее увеличение количества этапов связано со значительными вычислительными затратами и в настоящее время не представляется возможным. Однако можно предположить о характере процесса обучения при K ^да . Изменение порога для принятия ( к + 1)     „( к )

значений выходов нейронов с Доп — с ДоП будет стремиться к нулю. Это значит, что, обучившись примерам на предыдущем этапе, их количество, которое ошибочно распознается на текущем этапе, будет либо равно нулю, и после просмотра обучающего набора начнется следующий этап; либо число ошибочно распознаваемых примеров будет отлично от нуля, но достаточно мало, чтобы можно было говорить о том, что сеть будет корректировать свои параметры, исходя из наиболее плохо распознаваемых примеров, т.е. таких, для которых выходы нейронов последнего слоя имеют наиболее далекие значения от желаемых.

Таким образом, можно прийти к алгоритму обучения на худших примерах. Он заключается в том, чтобы на каждой эпохе обучения для корректировки параметров нейронной сети выбирать те примеры, для которых результат обработки сетью наиболее далек от желаемого. Следует заметить, что в случае такого отбора изменение порога допустимых значений нейронов выходного слоя теряет смысл, так как всегда из значений выходов нейронов, соответствующих классу образа, можно выбрать минимальное, а из значений выходов остальных нейронов выходного слоя – максимальное. Образы, соответствующие этим двум случаям, и являются распознаваемыми хуже, чем остальные.

Алгоритм обучения на худших примерах можно обобщить путем введения параметра: количество наиболее плохо распознаваемых примеров P , используемых в течение одной эпохи. Причин, по которым образ может быть отнесен к плохо распознаваемым, может быть две. Первая – недостаточно высокий уровень нейрона выходного слоя, соответствующего классу образа. Вторая – слишком высок уровень нейрона выходного слоя, не соответствующего классу образа. В связи с этим образы предлагается отбирать по отдельности в виде двух групп. Признаком включения образа в группу может служить тот факт, что соответствующий уровень нейрона выходного слоя отличается от желаемого на большую величину, нежели уровни нейронов, не включенных в группу. Таким образом, для определения примеров, входящих в группу худших из-за несоответствия выходного уровня нейрона соответствующего класса, необходимо вычислять на каждой эпохе обучения порог допустимого отклонения y д ⁺ _оп . Для определения примеров, входящих в группу худших из-за несоответствия выходного уровня нейрона, не соответствующего классу примера, необходимо вычислять на каждой эпохе обучения порог допустимого отклонения y д ^- _оп . В каждую группу должно попасть не менее P примеров. Всего на каждой эпохе обучения количество примеров, попавших в ту или иную группу, также получится не менее P .

Обучение на худших примерах, как и поэтапное, может происходить в комбинации с пакетным обучением.

Алгоритм пакетного обучения на худших примерах записывается следующим образом ( L – максимальный размер пакета):

задать cv = желаемое значение порога допустимости цикл: пока (y+доп < cv)или(y-доп < cv) определить y+доп и y-доп так, чтобы недопустимых примеров в каждой группе было не менее P цикл: для всех обучающих примеров если ответ недопустимый то вычислить ∆Wi если счетчик_НК=L то скорректировать параметры сети обнулить ∆W обнулить счетчик_НК иначе увеличить счетчик_НК ∆W←∆W+∆Wi если счетчик_НК>0 то скорректировать параметры сети

Результаты экспериментов

Поэтапное обучение

Для сравнения характеристик обучения нейронной сети по различным алгоритмам были проведены эксперименты по обучению распознаванию изображений цифр.

Так как обучение начинается с определения случайных величин в качестве начальных значений параметров, оно носит стохастический характер. Для получения результатов процедура обучения для каждого алгоритма выполнялась неоднократно при различных начальных условиях, а полученные характеристики усреднялись. Количество обучающих примеров было различным: данные приводятся для обучения по 50, 150, 500, 1500 и 5000 изображениям. В силу ограниченности системных ресурсов обучение большему числу изображений для экспериментов не использовалось. На практике в такой ситуации применяют дообучение по какому-либо алгоритму сети, натренированной на небольшом (несколько тысяч) количестве изображений.

Параметры, по которым сравнивались алгоритмы, следующие:

• 1.    частота обучения p нейронной сети при различных начальных условиях. Если обучение не приводило к улучшению результата в течение длительного периода, то считалось, что сеть не может обучиться. Частота обучения вычислялась как отношение числа успешных запусков к общему числу запусков на обучение;

• 2.    время обучения сети T (при успешном исходе обучения);

• 3.    количество корректировок параметров нейронной сети C за весь период обучения. Эта величина может характеризовать необходимое количество обменов данными между вычислительными процессами при распараллеливании обучения на кластерных вычислительных системах;

На рис. 1 приводятся зависимости времени обучения сети от количества дополнительных итераций K при поэтапном обучении для обучающих выборок различного размера.

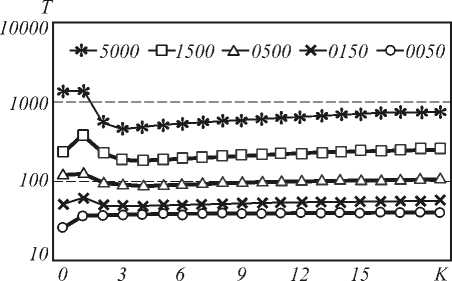
Рис. 1. Зависимость времени обучения нейронной сети T от количества дополнительных этапов K при выборочном (K=0) и поэтапном (K>0) обучении при различном количестве обучающих примеров

Время указано в секундах в логарифмическом масштабе. Точки с K=0 соответствуют выборочному обучению, остальные – поэтапному с соответствующим количеством дополнительных этапов K. За исключением выборки из 50 обучающих примеров при увеличении K, начиная с 1, время обучения снижается, достигая минимума при K=3 или K=4, затем линейно возрастает с небольшим коэффициентом пропорциональности. По сравнению с выборочным обучением поэтапное, при выборе оптимального K, происходит значительно быстрее (для 5000 примеров время обучения сокращается в 3 раза).

Как уже отмечалось, нейронная сеть не всегда может полностью научиться распознаванию обучающих примеров. Причина этого в локальности применяемого градиентного метода, который является основой метода обратного распространения ошибки. Поэтому необходимо обращать внимание не только на время обучения сети, но и на частоту нахождения решения при случайном выборе начальных условий.

На рис. 2 показана зависимость частоты удачного обучения p в процентах для различных алгоритмов и обучающих выборок. Обозначения те же, что и на рис. 1.

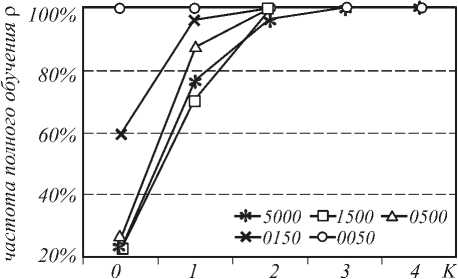
Рис. 2. Зависимость частоты полного обучения нейронной сети при выборочном (K=0) и поэтапном (K>0) обучении при случайном выборе начальных условий обучения

Частота полного обучения у поэтапного алгоритма в несколько раз больше, чем у выборочного. Условие преждевременной остановки обучения и принятия решения о невозможности дальнейшего улучшения оценки нейронной сети формировалось исходя из соображения, что время, затраченное на одну попытку обучения при неудачном исходе, должно быть во много раз больше, чем при удачном исходе. Следовательно, для уменьшения среднего времени, затраченного на получение нейронной сети, распознающей образы при заданном допуске значения оценки, поэтапное обучение является более эффективным.

Как показали эксперименты, число корректировок параметров нейронной сети резко снижается при введении нескольких этапов обучения (рис. 3). Начиная с K=3, число корректировок продолжает снижаться, стагнируя. Можно предположить, что при поэтапном обучении происходит более эффективный выбор направления оптимизации, что приводит к снижению общего числа шагов в пространстве параметров сети и снижению времени обучения.

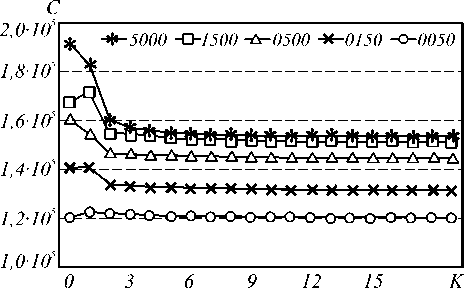
Рис. 3. Количество корректировок параметров нейронной сети за все время обучения при различном числе обучающих примеров

Пакетный режим

Применение пакетного обучения приводит к менее выраженным зависимостям сравниваемых параметров от максимального размера пакета L . Время обучения имеет слабую тенденцию к снижению, однако это изменение происходит нестабильно (рис. 4а). Частота обучения в целом с увеличением максимального размера пакета увеличивается, но при близких значениях L изменение не предсказуемо (рис. 4в). Единственный критерий, имеющий стабильную тенденцию к снижению – количество корректировок параметров сети, которое постоянно снижается (рис. 4б).

Т 200

-^-0500 -п-0150

а) 100 -]—

^х

О

1     4     7    10    13    16    19 L

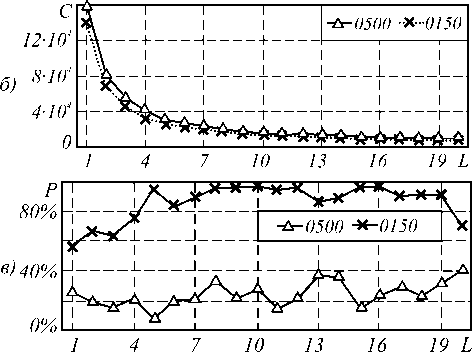
Рис. 4. Зависимость от максимального размера пакета: а) времени обучения;

б) числа корректировок; в) частоты обучения при пакетном обучении

Пакетный режим при поэтапном обучении

Относительно исходного выборочного обучения, поэтапное отличается введением дополнительного внешнего цикла. Пакетное обучение характеризуется наличием буфера, в котором накапливаются изменения параметров нейронной сети перед их корректировкой. Обе эти особенности не являются взаимоисключающими и могут быть использованы одновременно. Комбинированный алгоритм состоит в следующем.

задать минимальное значение с доп . цикл : до с доп >= c v

{ цикл: пока есть ошибки распознавания { цикл: для всех обучающих примеров если распознавание ошибочно то если счетчик_НК=L

{ скорректировать параметры сети обнулить счетчик_НК } иначе увеличить счетчик_НК если счетчик_НК>0

скорректировать параметры сети

} увеличить cдоп.

}

Этот алгоритм имеет уже два параметра, влияющих на процесс обучения: количество дополнительных этапов K и максимальный размер пакета L . Чтобы исследовать практическое влияние этих параметров на обучение, необходимо построить двумерную функцию, а для нахождения оптимальной комбинации для минимума времени обучения потребуется двумерная оптимизация с использованием алгоритмов глобальной оптимизации, так как зависимость по одному параметру не является гладкой (рис . 4). В силу ограниченности наличных системных ресурсов полномасштабный эксперимент такого рода провести в настоящее время не представляется возможным.

Предположим, что характер зависимости исследуемых критериев обучения сохраняется для каждого параметра комбинированного алгоритма при изменении другого. Тогда для нахождения оптимальной комбинации по времени обучения можно воспользоваться методом покоординатного спуска. В качестве первого шага воспользуемся полученными зависимостями при L=1 , соответствующими поэтапному обучению. Минимальное время обучения получается при K=3. Далее найдем зависимость времени обучения от максимального размера пакета при трех дополнительных этапах.

На рис. 5а показана зависимость времени обучения от величины L при K=3. Как и предполагалось, характер зависимости остался прежним: время обучения практически не изменяется.

Частота обучения осталась на уровне 100%: при всех начальных значениях параметров сеть обучалась полностью. Зависимость количества коррек- тировок имеет тот же характер, как при простом пакетном обучении (рисунок 5б).

т

ПО

a)

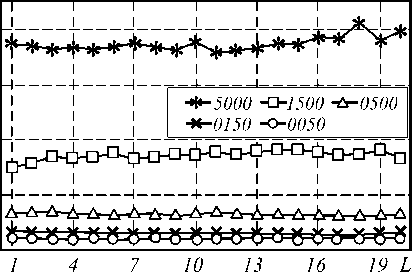
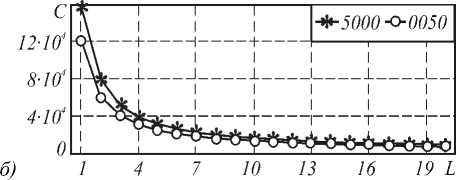
Рис. 5. Комбинированное обучение, K=3: а) время обучения; б) число корректировок параметров сети

Обучение на худших примерах

Проведенные эксперименты по обучению нейронной сети на худших примерах с параметрами P и L показали безусловное отставание по времени в сравнении с поэтапным обучением.

Зависимости частоты полного обучения при случайном выборе начальных параметров нейронной сети и времени обучения от числа отбираемых наиболее плохо распознаваемых примеров P показаны на рис. 6. Корректировка параметров нейронной сети производилась при L =1. С учетом того, что в случае невозможности научиться распознавать все обучающие примеры процесс обучения происходит значительно дольше, можно сделать следующее заключение. Оптимальным значением параметра P в представленных экспериментах является величина из диапазона 20..40, т.е. несколько десятков. При снижении этого значения время обучения сильно возрастает (в десятки раз), а при увеличении значительно снижаются шансы полностью обучить нейронную сеть (на десятки процентов).

Зависимость времени обучения и числа корректировок параметров нейронной сети при пакетном обучении на худших примерах от максимального размера пакета L оказалась такой же, как в случае поэтапного обучения. Частота полного обучения при увеличении L до некоторого значения остается на уровне 100% , затем начинает убывать, т.е. характер зависимости такой же, как при изменении величины P .

Таблица 1.

Сравнение различных методов обучения

Количество обучающих примеров Q	Минимальное время обучения T, с		Число корректировок параметров сети C
	ПО	ОХП	ПО	ОХП
150	48,5	57,3	133,8 • 103	137,8 • 103
500	88,2	188,4	146,2 • 103	97,6 • 103
1500	183,5	572,0	153,8 • 103	101,9 • 103
5000	456,7	1060,1	157,2 • 103	117,3 • 103

T 10000

100%

5 80%

§60%

S40%

§ 20%

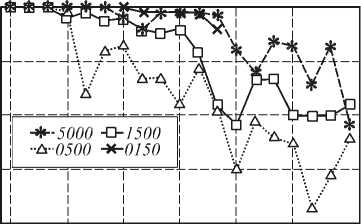
а)       1     30    60    90   200 350 P

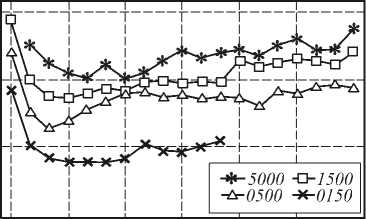
б)      1     30    60    90   200   350 P

Рис. 6. Зависимость частоты полного обучения (а) и времени обучения T (б) от параметра P при различном количестве обучающих примеров

В таблице 1 для сравнения приведены результаты обучения нейронной сети двумя алгоритмами: поэтапное обучение (ПО) и обучение на худших примерах (ОХП).

Данные приведены для случая L=1. Комбинирование любого из алгоритмов с пакетным обучением при увеличении размера пакета L приводит к снижению числа корректировок и слабому росту времени обучения.

По сравнению с поэтапным, обучение на худших примерах в целом привело к большим временным затратам, но меньшему числу корректировок параметров сети.

Заключение

Разработанные алгоритмы позволяют обучить нейронную сеть безошибочно распознавать все примеры из обучающего набора.

Поэтапное обучение по критерию минимальности времени обучения более эффективно, чем пакетное. При этом среднее число удачных исходов обучения при различных начальных условиях возрастает. Пакетное обучение значительно снижает количество корректировок параметров сети. Поэтапное обучение можно комбинировать с пакетным. При этом эффект от комбинации алгоритмов проявляется аддитивно.

Обучение на худших примерах приводит к большим временным затратам, но требует меньшего числа корректировок параметров сети.

Количество корректировок параметров сети имеет большое значение при распараллеливании алгоритмов для вычислительных систем типа кластеров. Оно определяет объем и частоту передачи данных, которыми необходимо обмениваться параллельно исполняющимся задачам. Снижение числа корректировок может привести к высокой эффективности распараллеливания алгоритмов.

Работа выполнена при поддержке грантов РФФИ (№ 01-01-00097 и № 03-01-00109), Президента РФ (№ НШ-1007.2003.01) и российско-американской программы «Фундаментальные исследования и высшее образование» («BRHE»).