Алгоритмы оценки наличия двух и более пиков в выборке данных фрагмента масс-спектра для программного обеспечения обработки масс-спектров в условиях недостаточного разрешения

Рассматриваются алгоритмы, позволяющие сделать оценку наличия двух и более пиков в выборке данных фрагмента масс-спектра. Необходимость разработки подобных алгоритмов возникает в связи с тем, что время выполнения программ оценки параметров наложившихся пиков существенно больше времени оценки параметров одиночных пиков, и есть смысл оперативно в режиме on-line выдать информацию о параметрах одиночных пиков, а затем в режиме off-line произвести разделение пиков и выдать окончательный результат.

Кл. сл. : методы обработки сигналов, масс-спектрометрия, оценка параметров пиков в мультиплетах

ПОСТАНОВКА ЗАДАЧИ

В настоящее время существует ряд различных методов оценки параметров отдельных масс-спектрометрических пиков, образующих мультиплет [1, 2, 3, 4]. Все методы разделения мультиплетов требуют гораздо больше машинного времени на обработку, чем оценка параметров в одиночном пике. Рассматриваются три типа алгоритмов, позволяющих ответить на вопрос, содержится ли во фрагменте масс-спектра одиночный пик или в нем два или более пика.

Первый тип алгоритмов основан на вычислении моментов третьего и четвертого порядков, позволяющих оценить эксцесс и асимметрию исходного сигнала.

Второй тип алгоритмов основан на вычислении сверток исходных данных с функциями, представляющими собой вторую и четвертую производную от функций, описывающих форму спектральных пиков. Если у обеих сверток в одной и той же точке имеются максимумы, то это значит, что на экспериментальной кривой в этом месте расположен пик, а в данной точке — его вершина. Использование подобных алгоритмов позволяет оценить наличие "мультиплетности" по количеству максимумов в сигналах после сверток, а также по отношению максимумов и минимумов в сигналах.

Третий тип алгоритмов основан на использовании разложения исходного сигнала на отдельные составляющие в приспособленном к обрабатываемым сигналам ортогональном базисе. В качестве базиса используется усредненный масс-спектр, в котором отсутствуют примеси — стандартный об- разец. Для такого масс-спектра в результате его разложения в приспособленном ортогональном базисе мы получаем единственную линию (начальную компоненту), если выборка данных содержит одиночный пик. Критериями для принятия решения о наличии мультиплетности является сравнение норм и квадратов максимальных значений начальных компонент в векторах, полученных в результате выполнения преобразования соответственно стандартного образца и тестируемых сигналов.

Указанные алгоритмы могут быть применены в программном обеспечении как в отдельности, так и в комплексе алгоритмов нескольких типов в разных комбинациях.

ВЫЧИСЛЕНИЕ МОМЕНТОВ ВЫСШИХ ПОРЯДКОВ

Использование моментов третьего и четвертого порядков исходного сигнала позволяет производить оценку наложения пиков. Наложение пиков приводит к асимметричности кривой, описывающей форму спектрального сигнала относительно оси, проходящей через центр тяжести. В первом приближении центральный момент третьего порядка при наложении пиков для симметричной функции, описывающей форму пика, должен быть отличен от нуля.

Вычисление параметра центра:

Z It

t = —---

0    Z I, ’

I_i — значения отсчетов на пике, t ₀ — положение центра, t_i — значения независимой переменной.

Центральный момент третьего порядка можно выразить через начальные моменты первых трех порядков:

ц ₃ = m 3 - 3 m 1 m 2 + 2 m 1 ³,

При y >  const₄ пики считаются наложившимися.

ВЫЧИСЛЕНИЕ СВЕРТОК С ПРОИЗВОДНЫМИ to

F n ( t i ) = J S .

-to

Г t   ) /tV

— t i I f\ I ^d t ,

l ^0   ) l Ц)

m ₃ , m ₂ , m ₁ — начальные моменты соответственно 3, 2 и 1-го порядков.

Оценку "наложенности" пиков можно сделать, вычислив безразмерную величину

где

S n

г t

l ^ 0

— весовые функции,

k = -3^.

µ ₂ ³

При k >  const₃ пики считаются наложившимися. Вычисление оценок начальных моментов производится по приближенным формулам:

N

^ k = M I ( t i - ^) ^k ,                  (2)

N i = 1

k = 1,2,3,4 — порядки моментов.

Кроме характеристики асимметрии для оценки наложения пиков можно также использовать коэффициент эксцесса, который вычисляется с помощью центрального момента четвертого порядка по следующей формуле:

l ^ 0

г t ) являющиеся производными от функции f — I, l ^ 0 ) описывающей стандартную форму пика единичной амплитуды и полушириной µ ₀ .

Для свертки со второй производной при A ²

— > 10, где A — амплитуда пика, а с ² — σ ²

дисперсия шумов для составного пика (совокупность наложившихся пиков), должно выполняться неравенство: пик составной, если

R = | d 0 - d 1| >  const 1 ,                   (5)

где d 0 и d 1 — минимумы второй производной свертки (см. рис. 1). Для свертки с четвертой производной признак наложения (рис. 2):

Y = -^ - 3.                   (3)

µ ₂ ²

R i = | d 0 - d 1| >  const₂.                (6)

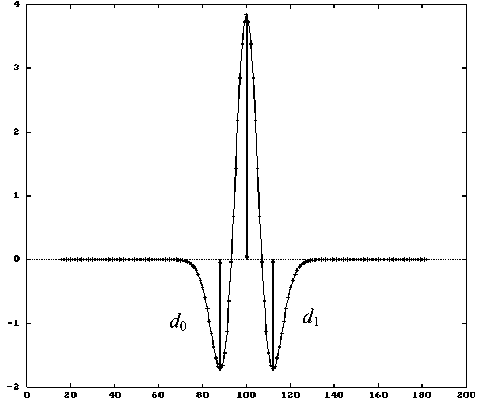
Рис. 1. Признак наложения линий по свертке со второй производной базовой (аппаратной) функции (одиночный пик)

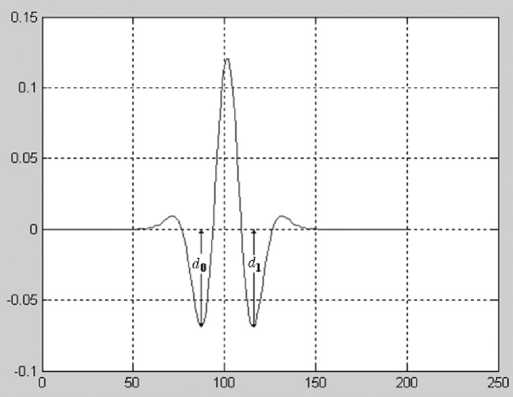
Рис. 2. Признак наложения линий по свертке с четвертой производной базовой (аппаратной) функции (одиночный пик)

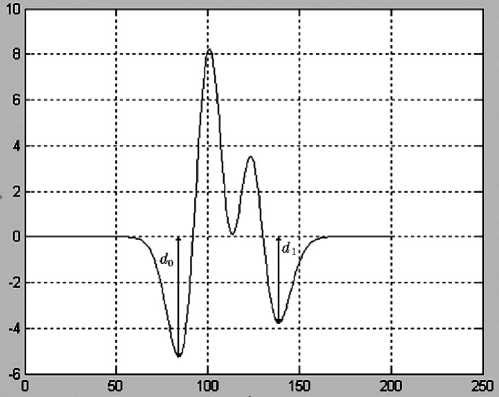
Рис. 3. Признаки наложения по свертке со второй производной (наложившиеся пики): минимумы различны, максимумов больше одного

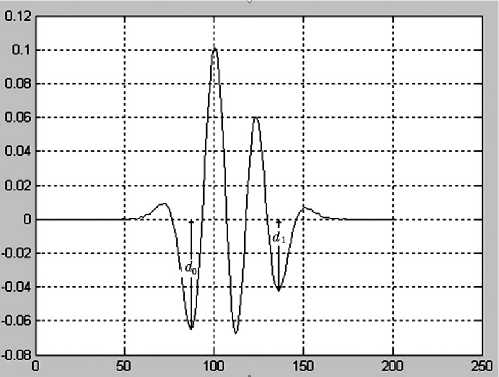
Рис. 4. Признаки наложения по свертке с четвертой производной (наложившиеся пики): минимумы различны, максимумов больше одного

Кроме того, пик составной, если в свертке со второй производной больше одного максимума, а для свертки с четвертой производной — больше трех максимумов.

На рис. 1–4 показаны значения минимума d ₀ и минимума d ₁ для гауссовых пиков.

Значения const1 и const2 вычисляются из функций, описывающих форму пика, и отношения сигнала к шуму.

ИСПОЛЬЗОВАНИЕ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ В СИСТЕМЕ БАЗИСНЫХ ФУНКЦИЙ (СБФ)

Сущность алгоритмов заключается в выполнении следующей последовательности операций [5, 6, 7].

• 1.    Выполняем синтез целевого оператора H ортогонального преобразования Y = H X в приспособленном базисе. В качестве исходных данных для такого синтеза берется вектор цифровых значений функции, описывающей форму пика, например гауссова, или форму пика по экспериментальным данным .

• 2.    Организуем скользящее окно шириной N , где N — длина вектора исходного сигнала, по которому был найден оператор преобразования H.

• 3.    Для каждого вектора исходного сигнала в окне ( F 1 ) находим вектор преобразованного сигнала в приспособленном базисе Y = H F ₁^T . После спектрального преобразования в приспособленном базисе спектр сигнала в ортогональном базисе, построенном на основе формы самого сигнала, представляет собой одиночную линию, аналогично то-

• Рис. 5. Спектр одиночного пика в приспособленном базисе для N = 64

• 4.    Сравниваем с порогом величину Y (1) для преобразованных данных каждого текущего окна. При превышении величины Y (1) порога считаем, что пик обнаружен.

му как спектр функции у = cos( ωt ) в традиционном гармоническом базисе представляет одиночную линию, например Y (1) на рис. 5.

На рис. 5 представлен спектр сигнала одиночного пика с единичной амплитудой. На рис. 6 представлены два наложившихся пика масс-спектра. На рис. 7 представлен спектр сигналов двух наложившихся пиков масс-спектра, представленных на рис. 6.

Преимуществом данного алгоритма является

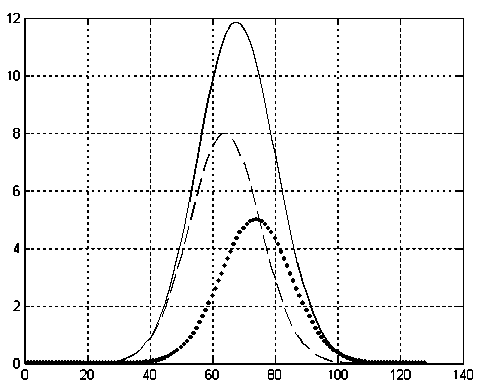
Рис. 6. Наложившиеся пики гауссовой формы. Сплошная линия — cуммарный сигнал, пунктирная линия — сигнал F 1 , линия из точек — F 2

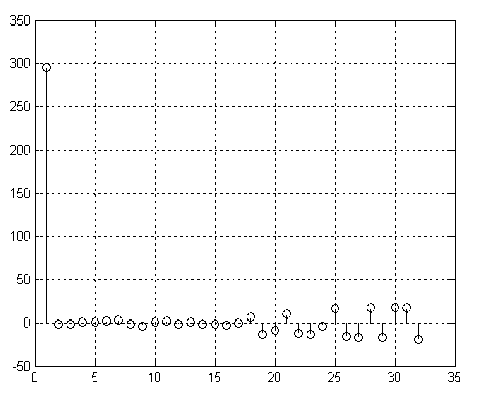
Рис. 7. Сигнал суммы F1 + F2 пиков гауссовой формы после спектрального преобразования в приспособленном базисе его способность автоматически принимать решение о том, что обнаруженный пик состоит из двух или более наложившихся пиков. Для выполнения этой операции необходимо оценить близость полученного в результате преобразований вектора Y c аналогичным вектором Yэт, который характеризует одиночный пик. Например, в случае наложения двух пиков, представленных на рис. 6, преобразованный сигнал содержит дополнительные составляющие, кроме основной линии Y(1), как показано на рис. 7. Оценка близости двух векторов производится путем сравнения с порогом разности норм и (или) сравнения с порогом разности квад- ратов основных линий или по другим критериям, которые подробно описаны в [5, 6, 7]. Например, вектор Y, полученный в результате преобразования исходного сигнала в приспособленном базисе, принадлежит классу одиночных пиков, если

P 1 = II Y - Y_эт II ≤ δ ,                   (7)

P 2 = Y (1)² - Y эт (1)²I ≤ ε .             (8)

В противном случае Y принадлежит классу сигналов "наложившиеся пики". Параметры порогов δ и ε выбираются в процессе обучения с использованием информации о функции, описывающей форму пика.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ АЛГОРИТМОВ НА МОДЕЛЯХ СИГНАЛОВ, СОДЕРЖАЩИХ НАЛОЖИВШИЕСЯ ПИКИ

Для определения возможностей указанных алгоритмов с помощью вычислительного эксперимента определялись параметры наложения пиков, которые вычислялись по приведенным выше формулам для сигналов в дублетах с соотношением амплитуд отдельных пиков 5 : 1 в отсутствие шума и с шумом (соотношение сигнал/шум S/N) при различных степенях наложения M для пиков гауссовой формы. Степень наложения M определяется как отношение полуширины пика к расстоянию между пиками в дублете; M = ∞ соответствует одиночному пику, S/N = ∞ соответствует сигналам без шума. Данные экспериментов без шума представлены в табл. 1. В табл. 2 представлены данные при различных степенях наложения при S/N = 100.

Анализ результатов, приведенных в табл. 1 и 2, показывает, что при отсутствии шума все рассмотренные алгоритмы позволяют оценивать наличие мультиплетности в обрабатываемых данных. Вычисление момента 3-го порядка и нормы вектора данных, полученного в результате преобразования с помощью ортогональных СБФ, позволяет оценить степень наложения как при наличии, так и при отсутствии шума.

ЗАКЛЮЧЕНИЕ

• 1.    Рассмотренные алгоритмы каждого типа могут быть применены в программном обеспечении как по отдельности, так и в комплексе алгоритмов, состоящем из нескольких типов в разных комбинациях.

• 2.    Алгоритм, основанный на вычислении момента 3-го порядка, и алгоритм вычисления нормы вектора, полученного в результате разложения

Табл. 1. Параметры наложения, вычисленные по предлагаемым формулам, при различной близости одиночных пиков в отсутствие шума

№ п/п	Алгоритм	Формула	Параметры наложения при различной близости ( M ) пиков при отсутствии шума
			M = ∞	M = 20 000	M = 2000	M = 500
1	Момент 3	1	3.5E-015	1.04E-004	0.0010	0.0042
2	Момент 4	3	1.7523	1.7523	1.7523	1.7523
3	Свертка с 2-й производной	5	3.5E-015	7.78E-005	1.18E-004	0.0034
4	Свертка с 4-й производной	6	0	2.65E-007	1.15E-006	3.23E-006
5	СБФ	7	0.0041	0.0043	0.0170	0.0670
6	СБФ	8	6.5E-004	7.1E-004	7.91E-004	1.69E-004

Табл. 2. Параметры наложения, вычисленные по предлагаемым формулам, в присутствии шума

№ п/п Алгоритм Формула Средние значения параметров наложения при различной близости пиков(M) при S/N = 100 M = 20 000 M = 2000 M = 500 M = 10 1 Момент 3 1 0.001 0.0014 0.0040 0.21 2 Момент 4 3 1.7523 1.7523 1.7523 1.7636 3 Свертка с 2-й производной 5 0.0430 0.0234 0.0261 0.07 4 Свертка с 4-й производной 6 1E-005 1E-005 1.3E-005 1.7E-005 5 СБФ 7 0.2 0.22 0.24 3.31 6 СБФ 8 0.02 0.04 0.06 0.08 с помощью ортогональных СБФ, позволяют оценить не только сам факт наличия "мультиплетно-сти", но и степень наложения как при наличии, так и при отсутствии шума.