Алгоритмы оптимальной реконфигурации распределительной сети

Сегодня одной из проблем электросетевого комплекса России является повышение экономичности и надежности обеспечения условий для реализации рыночных отношений между поставщиками и потребителями электрической энергии путем оптимального управления потоками энергии. Эта и другие проблемы в электросетевом комплексе России вызвали необходимость создания соответствующей технологической платформы «Интеллектуальные энергетические системы России», целью которой является содействие внедрению в российской электроэнергетике интеллектуальных технологий и формирование «умной» электрической сети.

Одной из основных задач Платформы является разработка распределенных интеллектуальных систем управления, работающих в режиме реального времени и позволяющих реализовать новые алгоритмы и методики управления энергосистемой, включая управление её активными элементами.

Сегодня в этом направлении сделано достаточно много, но в основном в оснащении объектов энергосистемы средствами информационного обеспечения и разработке силового оборудования, позволяющего адаптивно влиять на распределение потоков энергии преимущественно в магистральных электрических сетях. В этих сетях достигнута высокая наблюдаемость режима и вводятся пилотные образцы установок адаптивного управления на базе силовой полупроводниковой техники.

Решение задачи реконфигурации распределительной сети

В распределительных сетях напряжением 6, 10 и 35 кВ решение проблемы интеллектуализации управления осложняется большой размерностью системы, низкой наблюдаемостью режима и огра- ниченным пока набором типов технических средств адаптивного управления, включающем РПН трансформаторов питающих центров, коммутационные аппараты с дистанционным управлением, интеллектуальные вакуумные выключатели – реклоузеры [1] и устройства компенсации реактивной мощности. Дополнительные возможности появляются и в связи с устойчивыми тенденциями развития систем распределенной малой генерации. Но, с другой стороны, здесь для оценки состояния системы и ее режима, без компьютерного анализа которого невозможно принятие оптимального управления, могут использоваться простые методы расчета режима, учитывающие разомкнутый характер эксплуатационных схем распределительной сети [2].

Особенностью конфигурации исходной сети является высокий коэффициент связности, определяемый отношением числа ветвей и узлов графа сети, что обеспечивает многовариантность построения возможных деревьев на исходном графе. Оптимальные места размыкания размещаются в точках потокораздела исходной замкнутой сети, определяемых по результатам расчета потокорас-пределения в R-схеме.

Однако можно гораздо проще определить оптимальную конфигурацию распределительной сети путем анализа режима исходной разомкнутой сети. Расчетная схема такой сети имеет одну точку поставки электроэнергии, обычно фиктивный узел, от которого запитаны силовые трансформаторы центров питания распределительной сети. Алгоритмизация расчетов разомкнутых электрических сетей производится на основе информационной модели, содержащей данные о конфигурации сети, о параметрах схемы замещения ветвей, о расчетных нагрузках узлов. Конфигурация сети задается расчетными номерами NHv, NKv и NLr, NPr узлов начала и конца для каждой ветви v и каждого разреза r. Положительное направление ветвей определяется направлением питания узлов сети от ЦП. Местоположение NLr и NPr относительно друг друга безразлично. Расчетная нумерация узлов не допускает повторений. В принципе все узлы могут обозначаться принятыми эксплуатационными обозначениями, но при этом высока вероятность ошибок при формировании информационной модели.

Такое представление конфигурации сети не содержит параметра структурной связи, подобного матрицам инциденций. Использование метода адресных отображений [3, 4] позволяет на основе исходного представления конфигурации в виде массивов NH, NK и NL, NP определить параметр связи в форме адресных отображений. Заметим, что все узлы расчетной схемы в силу разомкнутого характера эксплуатационной схемы сети встречаются только один раз в массиве NK в отличие от массива NH. В этом случае последовательность порядковых номеров j узлов называют первым адресным отображением массива NK. Аналогично, порядковые номера i начальных узлов ветвей будут первыми адресными отображениями массива NH. Если все адреса массива NH заменить отображением j при условии NHi=NKj, то адреса i можно рассматривать как второе адресное отображение массива NH2 (рис. 1).

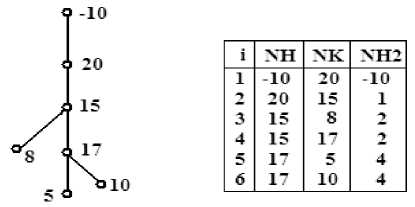
Рис. 1. Формирование адресных отображений

Аналогичным образом определяются и вторые адресные отображения разрезов. Так, для разреза NL α , NP β замена узлов их вторыми адресными отображениями NK определяется по условиям NL α = NKj и NP β = NKj. Связь содержимого ячеек массивов с их адресными отображениями выражается посредством штрих-функций.

Например, для ветви с адресом 5 связь начального номера 17 с питающей ветвью 15-17 определяется штрих-функцией первого ранга ′ i (5)=4. Вторичная операция «штрих» при аргументе ′ i (5) приводит к образованию штрих-функции второго ранга ² i ( ′ i (5))=2 и т. д. Таким образом, формируется весь ствол питания любого узла, ограниченный достижением во втором адресном отображении признака питающего центра. Применение вторых адресных отображений и штрих-функций позволяет избежать использования матриц инциденций и тем самым упростить алгоритмизацию расчетов в разомкнутых распределительных сетях.

Задача оптимальной реконфигурации сети может решаться методом покоординатного дискретного спуска посредством поочередной оптимизации каждого разреза в отдельности при фиксированных положениях остальных. Однако такой подход позволяет решить задачу лишь частично, однократное перемещение текущего разреза в оптимальное положение может сделать неоптимальными ранее найденные положения некоторых других разрезов. Поэтому покоординатный спуск должен быть циклическим и продолжаться, пока значение целевой функции в очередном цикле не совпадет с предыдущим.

Процесс оптимизации по критерию минимума потерь активной мощности начинается с расчета режима в R-схеме сети при заданных узловых токах. Оптимальное положение каждого разреза NL α , NP β и направление перемещения его на соседний участок влево или вправо определяется уровнями напряжения в узлах U α и U β . Если разница напряжений меньше заданной точности, то положение разреза можно считать оптимальным. При U α > U β нужно переместить через узел α в соседнюю ветвь. В случае U α < U β перемещение идет в противоположную сторону. После каждого переноса путем корректировки информационных массивов для изменившейся схемы вновь считается режим с последующей оценкой уровней напряжения для нового положения разреза. Если точность по разности напряжений достигнута, то осуществляется переход к оптимизации следующего разреза. При сохранении первоначального соотношения напряжений выполняется очередной переход в том же направлении. При изменении соотношения сравниваются потери мощности, и осуществляется переход к следующему разрезу из текущего состояния или предыдущего. В алгоритме предусмотрена возможность исключения из оптимизации разрезов, положение которых фиксируется по условиям надежности или резервирования выводимых в ремонт участков сети.

Реализация алгоритма проведена в среде графического программирования LabVIEW. Алгоритмы представлены на рис. 2 и 3.

При алгоритмизации внутреннего цикла (см. рис. 3) использованы подпрограмма определения пункта питания контура, образуемого оптимизируемым разрезом, и подпрограмма переноса разреза в соседнюю правую или левую ветвь. На рис. 4 показана фронтальная панель с исходными данными и результатами оптимизации простой разомкнутой сети, расчетная схема которой приведена на рис. 5. Оптимальная конфигурация найдена на первом цикле, второй цикл подтвердил результат.

На рис. 5, в показан результат переноса третьего разреза, увеличившего потери путем размыкания ветви 24-28. Для проверки влияния очередности оптимизации разрезов на результат были рассмотрены все 6 возможных комбинаций, и в каждой был получен одинаковый результат.

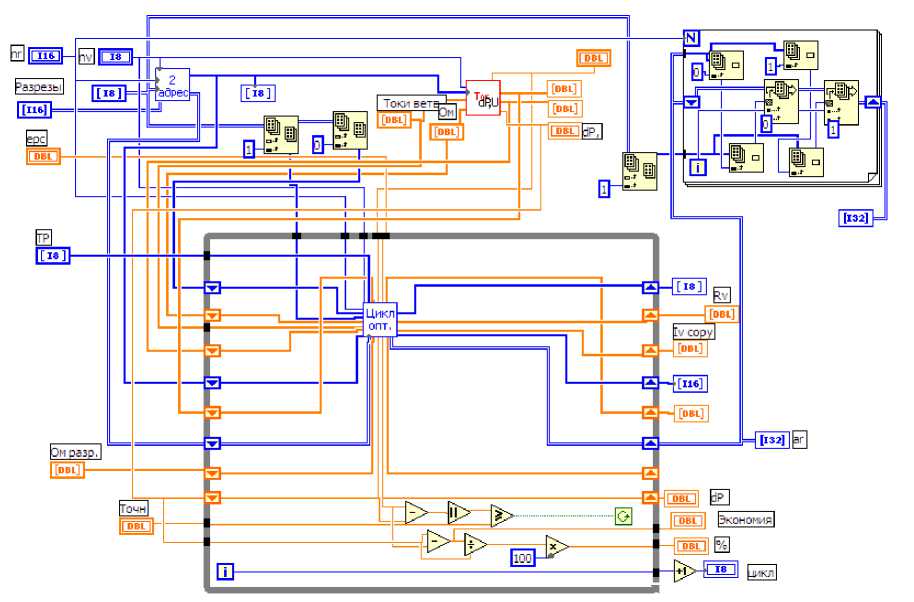
Рис. 2. Блок- диаграмма внешнего цикла оптимизации

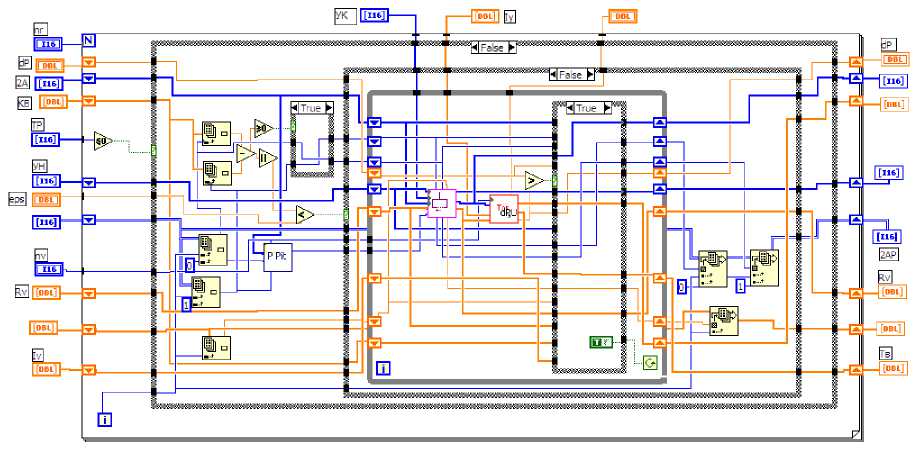
Рис. 3. Блок-диаграмма подпрограммы цикла оптимизации разрезов

Задача поиска оптимальной рекомбинации актуальна и для планирования режимов при выводе в ремонт участков сети. Первоначально для каждого выводимого в ремонт участка выбирается ближайший резервирующий разрез. Для этого организуется цикл по разрезам, в котором для каждого разреза путем просмотра стволов питания для узлов α и β определяется ранг штрих-функции до совпадения текущей ветви с ремонтируемой, если она принадлежит стволу. Перемещение по стволу ограничивается достижение пункта питания контура. После завершения цикла сформированный информационный массив позволяет выявить ближайший разрез и перенести его на место выводимой в ремонт ветви. После этого для сформированной расчетной схемы определяется оптимальная конфигурация. Этапы работы алгоритма для ремонта ветви 30-11 показаны на рис. 6.

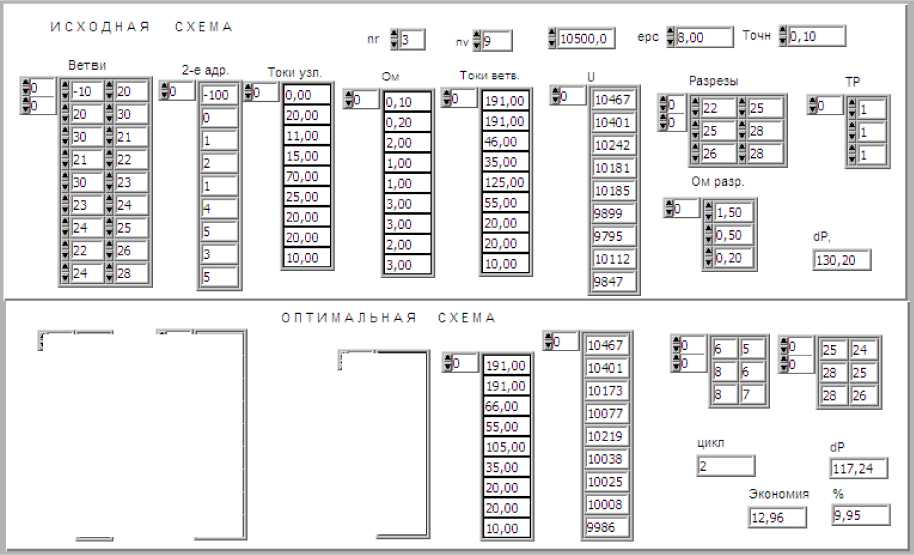
Рис. 4. Фронтальная панель

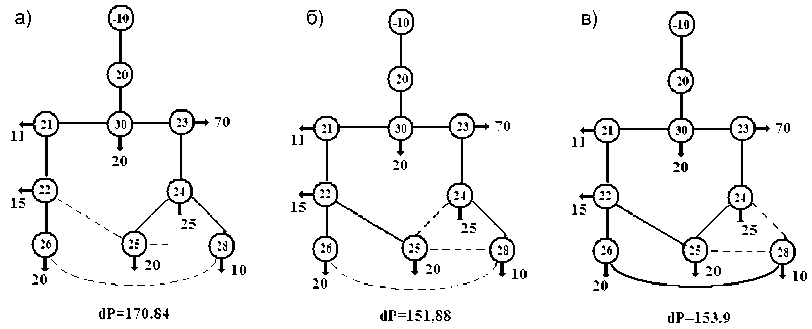
Рис. 5. Выбор оптимальной конфигурации сети

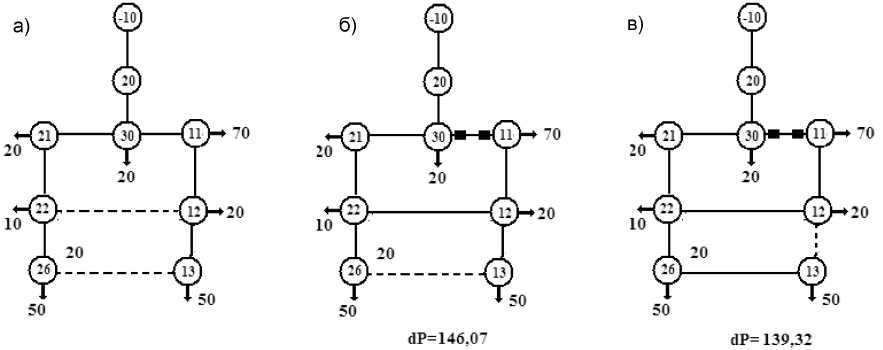
Рис. 6. Выбор оптимальной схемы ремонта ветви: а) исходная схема, б) расчетная схема, в) оптимальная схема

Заключение

Предлагаемые алгоритмы могут найти применение при разработке информационно-вычислительных комплексов для распределительных сетей крупных населенных пунктов, промышленных предприятий и других систем электроснабжения. Применимы они и для систем мультиагентного управления интеллектуальными распределительными сетями.