Алгоритмы построения цифрового двойника установки распределенной генерации

Цитирование: Булатов, Ю.Н. Алгоритмы построения цифрового двойника установки распределенной генерации / Ю.Н. Булатов, А.В. Крюков // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(6). С. 677-689. DOI: 10.17516/1999-494X-0256

необходимые данные, характеризующие функционирование физического объекта или системы [15–19]. Цифровой двойник включает детальную математическую модель, параметры которой уточняются с помощью информации, поступающей от измерительно-информационных систем.

Кроме понятия «цифровой двойник» используется термин «цифровая тень», определяющий наличие связей и зависимостей, описывающих поведение реального физического объекта и содержащихся в больших данных (big data), получаемых от реального объекта при помощи средств промышленного интернета [15]. Цифровая тень позволяет прогнозировать поведение реального объекта, но только в тех условиях, в которых осуществлялся сбор данных, что является основным ее отличием от цифрового двойника.

Создание цифрового двойника реального электроэнергетического оборудования или системы электроснабжения должно базироваться на применении различных датчиков для уточнения математической модели, а также на использовании интернета вещей (IoT) и систем сбора данных для их последующей обработки на основе интеллектуальных технологий.

В статье представлены основные положения концепции построения цифрового двойника установки РГ, работающей на основе синхронного генератора, оснащенного нечетким блоком автоматической настройки регуляторов возбуждения (АРВ) и скорости (АРС) вращения ротора [20]. Рассмотрена структура цифрового двойника в виде многосвязной модели, использующей экспериментальные данные. Представлены результаты компьютерных исследований по получению оптимизированной нейро-нечеткой модели регулирования скорости вращения ротора генератора.

Описание концепциии структуры построения цифрового двойника установки РГ

В качестве объекта, для которого предлагается построение цифрового двойника, рассмотрим турбогенераторную установку небольшой мощности, реализованную на основе неявнополюсного синхронного генератора. Малая постоянная инерции ротора требует учета при настройке взаимного влияния АРВ и АРС. Кроме того, для оптимального управления необходимо корректировать настройки регуляторов при значительных изменениях режимов работы установок РГ или электроэнергетической системы (ЭЭС) при параллельной работе РГ и ЭЭС. Выполнить эти требования возможно путем использования интеллектуальных алгоритмов управления. На рис. 1 представлена структурная схема установки РГ [20].

Принцип действия рассматриваемой системы управления заключается в идентификации режима работы установки РГ и коррекции коэффициентов настройки регуляторов в случае существенных изменений режимов. Для идентификации предложено использовать адаптивную сеть на основе системы нечеткого вывода (ANFIS), представляющую собой один из вариантов гибридных нейро-нечетких сетей. В целом ANFIS реализует систему нечеткого вывода Сугено в виде пятислойной нейронной сети прямого распространения сигнала [21]. Задача идентификации режима, решаемая блоком ANFIS, описана в [20].

Нечеткий регулятор с блоком автонастройки представляет собой систему нечеткого логического вывода с модулями идентификации цифровой модели установки РГ и согласованной настройки АРВ и АРС [20]. Применение согласованной настройки [22] позволяет сформировать начальную базу знаний fuzzy-регулятора. Затем модуль идентификации на основе экспе- – 679 –

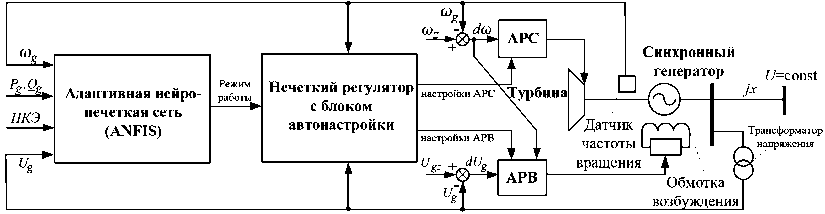
Рис. 1. Структурная схема адаптивной системы управления АРВ и АРС установки РГ: ПКЭ – показатели качества электроэнергии

Fig. 1. Structural scheme of adaptive system for control AVR and ASR of the DG plant: PQI – power quality indicators риментальных данных формирует цифровую тень для дальнейшего формирования цифрового двойника.

Предлагаемая концепция основана на представлении объекта в виде многосвязной структуры, имеющей определенное число входных и выходных параметров и связей, формируемых на основе экспериментальных данных. Предлагаемая структура цифрового двойника представлена на рис. 2. При необходимости добавления других контролируемых параметров предлагаемую структуру можно модернизировать.

Основные элементы установки РГ, такие как регуляторы, турбина, система возбуждения, представлены в виде нечетких моделей, определяющих зависимости входных и выходных переменных на основе нечеткого логического вывода. Отдельные связи параметров синхронного генератора также представлены в виде блоков нечеткого логического вывода ( S ₁, S ₂, S ₃, S ₄, S ₅), в совокупности образующих иерархическую нечеткую модель генератора. Элементы установки РГ позволяют адекватно описывать зависимости входных и выходных переменных, используя небольшое количество правил. В целом построение всей совокупности связей предлагаемой структуры основано на применении иерархических нечетких систем логического вывода [23], что позволяет значительно уменьшить размерность базы нечетких правил.

Для уменьшения объема баз правил отдельных блоков установки РГ предлагается использовать метод субтрактивной кластеризации [24] и адаптивную сеть ANFIS, позволяющие на основе получаемых экспериментальных данных от датчиков обучать нейронные сети, синтезировать и обновлять базы знаний нечетких систем. Согласно предлагаемой структуре датчики должны измерять все указанные на рис. 2 параметры. Измерительная система должна обеспечивать определение показателей качества электроэнергии. Для обучения и обновления нечетких моделей измерение параметров необходимо производить в переходных процессах, вызванных изменением режима работы установки РГ в процессе эксплуатации, а также при подаче на выходы регуляторов специальных пробных сигналов малой интенсивности, не нарушающих нормальной эксплуатации. При обновлении нечетких моделей выполняется оптимизация параметров функций принадлежностей терм-множеств и уменьшение, при возможности, числа нечетких правил.

Построение оптимизированной нечеткой модели отдельной связи цифрового двойника включает следующие шаги:

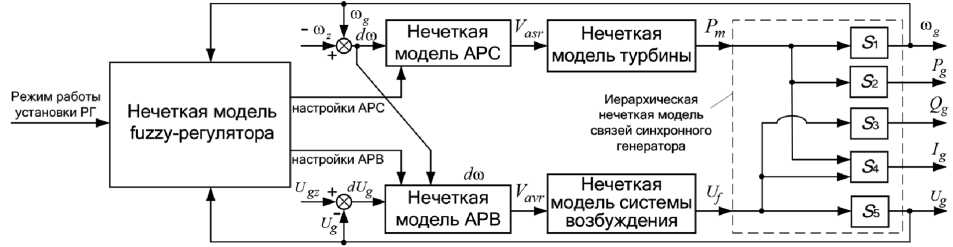
Рис. 2. Структура цифрового двойника установки РГ: w _z , w _g – соответственно, заданное и текущее значения скорости вращения ротора; d w – отклонение скорости вращения ротора от заданного значения; U_gz , U_g – соответственно, заданное и текущее значения напряжения генератора; dU_g – отклонение напряжения генератора от заданного значения; V_asr , V_avr – соответственно, сигналы управления от АРС и АРВ; P_m – механическая мощность на валу турбины; U f – напряжение на обмотке возбуждения генератора; P g , Q g – активная и реактивная мощности генератора; I g – ток генератора

Fig. 2. The structure of DG plant digital twin: w z , w g – accordingly, the set and current values of rotor rotational frequency; d w – the deviation of rotor rotational frequency from the set value; U gz , U g – accordingly, the set and current values of the generator voltage; dU g – the deviation of the generator voltage from a predetermined value; V asr , V avr – accordingly, the control signals from AVR and ASR; P m – mechanical power on the turbine shaft; U f – voltage of the generator excitation winding; P g , Q g – the generator active and reactive powers; I g – generator current

• 1.    Снятие экспериментальных данных.

• 2.    Обучение нейронной сети по полученным экспериментальным данным.

• 3.    Перевод данных «вход-выход» обученной нейронной сети в нечеткие переменные.

• 4.    Построение базы знаний нечеткой модели с использованием обученной нейронной сети и метода субтрактивной кластеризации.

• 5.    Использование генетического алгоритма (ГА) для оптимизации параметров функций принадлежности терм-множеств нечеткой модели.

Для описания термов базы знаний может быть использована гауссовская функция принадлежности

| х—с

,                                                                                    (1)

где с - координата максимума функции принадлежности; о - среднее квадратичное отклонение, которое определяет ширину функции; x – значение переменной из базового множества.

Процедура оптимизации функций принадлежности заключается в переборе различных значений параметров и оценивании разности между реакциями нечеткой модели и эталонными значениями (экспериментальными данными). При использовании ГА параметры функции принадлежности представляют в хромосоме вещественными числами или двоичными последовательностями с применением одного из известных методов кодирования. Затем к полученной популяции особей применяют процедуру ГА. Блок-схема описанного алгоритма оптимизации функций принадлежности нечеткой модели изображена на рис. 3.

На первом этапе выполняют конструирование нечеткой модели для различных значений параметров функций принадлежности где Un – вектор значений входной лингвистической переменной размерностью n; Yn – вектор значений выходной лингвистической переменной такой же размерности; n – общее число строк в нечеткой базе знаний; C – вектор значений параметров функций принадлежности, которые необходимо оптимизировать.

Определение функции приспособленности особей осуществляют по разности между реакциями нечеткой модели и экспериментальными данными с помощью следующего квадратичного критерия:

, (3) z=l где Def - оператор дефаззификации, выполняющий перевод нечетких переменных при соответствующих параметрах функций принадлежностей в конечные значения выходных параметров модели; yt - значения выходных параметров экспериментальных данных при соответствующих входных воздействиях.

В качестве генетических операторов используют отбор, скрещивание и мутацию осо-бей.

Для построения и оптимизации нечеткой модели разработана программа, имеющая Windows - ориентированный интерфейс, в которой реализуются описанные выше алгоритмы [25]. Далее при построении и оптимизации нечеткой модели используют указанную программу.

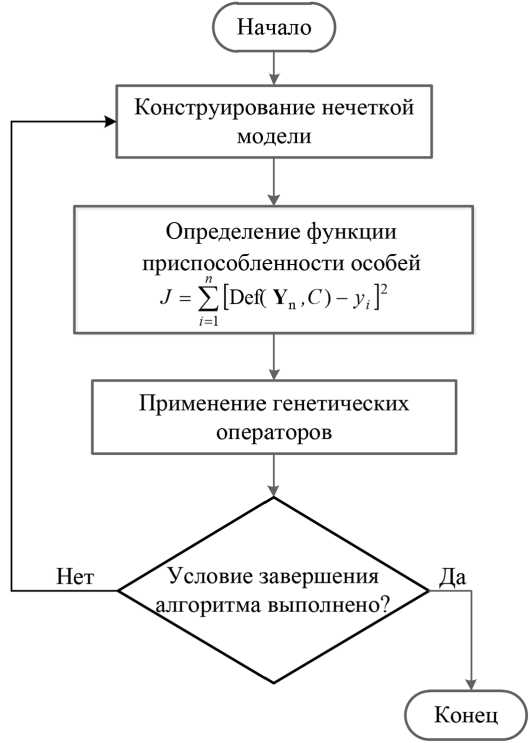
Рис. 3. Блок-схема алгоритма оптимизации функций принадлежности нечеткой модели

Fig. 3. Block diagram of the algorithm for optimizing the membership functions of a fuzzy model

Результаты моделирования

Исследования проводили на компьютерной модели турбогенераторной установки с АРВ и АРС мощностью 3125 кВ×А и напряжением 10 кВ, имеющей связь с электроэнергетической системой. Модель выполнена в системе MATLAB. Для исследования предлагаемых алгоритмов построения и оптимизации нечеткой модели были сохранены входной и выходной сигналы, соответствующие механической мощности на валу турбины и скорости вращения ротора генератора. Экспериментальные данные снимали в режиме подключения дополнительной нагрузки (рис. 4). Полученные при моделировании данные использовали для обучения нейронной сети и формирования правил базы знаний нечеткой модели. Неоптимизированная нечеткая модель при испытании дает отклик, показанный на рис. 4 б , где видно некоторое отклонение от экспериментальной характеристики.

Проведение процедуры оптимизации функций принадлежности и минимизации числа правил позволяет получить отклик нечеткой модели практически совпадающий с эталонны-

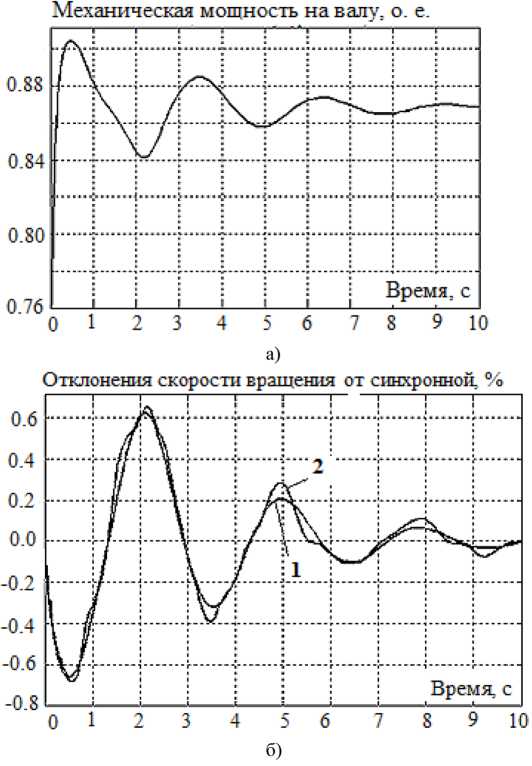
Рис. 4. Характеристики входного (а) и выходного сигналов (б): 1 – экспериментально полученная (эталонная) характеристика скорости вращения ротора генератора; 2 – характеристика скорости, сформированная с помощью системы нечеткого логического вывода

Fig. 4. Characteristics of the input (a) and output signals (б): 1 – experimentally obtained (reference) characteristic of the generator rotor speed; 2 – speed characteristic generated using a fuzzy inference system

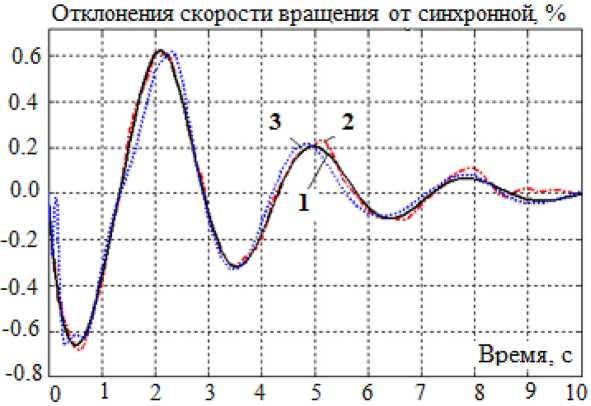
Рис. 5. Характеристика скорости вращения ротора генератора при подключении дополнительной нагрузки: 1 – экспериментальные данные; 2 – нечеткая оптимизированная модель без использования метода субтрактивной кластеризации (91 правило); 3 – нечеткая оптимизированная модель с использованием метода субтрактивной кластеризации (8 правил)

Fig. 5. The characteristic of the rotation rotor speed of the generator when connecting an additional load: 1 – experimental data; 2 – fuzzy optimized model without using the method subtractive clustering (91 rules); 3 – fuzzy optimized model using the subtractive clustering method (8 rules)

ми значениями. Сравнительный анализ осциллограмм выходного сигнала построенной оптимизированной модели показывает приемлемую точность в случае использования метода субтрактивной кластеризации, который также позволяет уменьшить количество терм-множеств и число правил нечеткой модели (рис. 5).

Построение и оптимизацию нечеткой модели выполняли также для физической модели, фото и функциональная схема которой показаны на рис. 6. Эта модель установки РГ включала в себя следующие элементы: синхронный генератор; машину постоянного тока, используемую в качестве первичного двигателя; возбудитель; преобразователь угловых перемещений; активноиндуктивную нагрузку. Скорость вращения ротора регулировали с помощью модели АРС в виде пропорционально-интегрально-дифференциального (ПИД) регулятора, реализованного с использованием блоков библиотек Real-Time Windows Target и Simulink системы MATLAB. Измерение скорости вращения ротора выполняли с помощью датчика угловых перемещений. Модель АРВ также выполнена в виде ПИД-регулятора. Связь между физической моделью и компьютером осуществляется через плату ввода-вывода типа PCI 6024Е (рис. 7). Для управления физической моделью в системе MATLAB была собрана схема (рис. 8), где модели регуляторов (блоки ARS и ARE) получали сигналы действующих значений тока, напряжения и скорости вращения ротора с помощью блока Analog Input. Действующие значения тока и напряжения определяли с помощью стандартных блоков RMS. Сигналы регулирования через блок Analog Output поступали на источник питания машины постоянного тока (для регулирования скорости вращения ротора) и возбудитель синхронной машины (для регулирования напряжения генератора).

Регистрация экспериментальных данных выполнена с помощью блоков Scope при различных уставках и коэффициентах настройки регулятора скорости. Полученные при этом осциллограммы скорости вращения ротора генератора представлены на рис. 9.

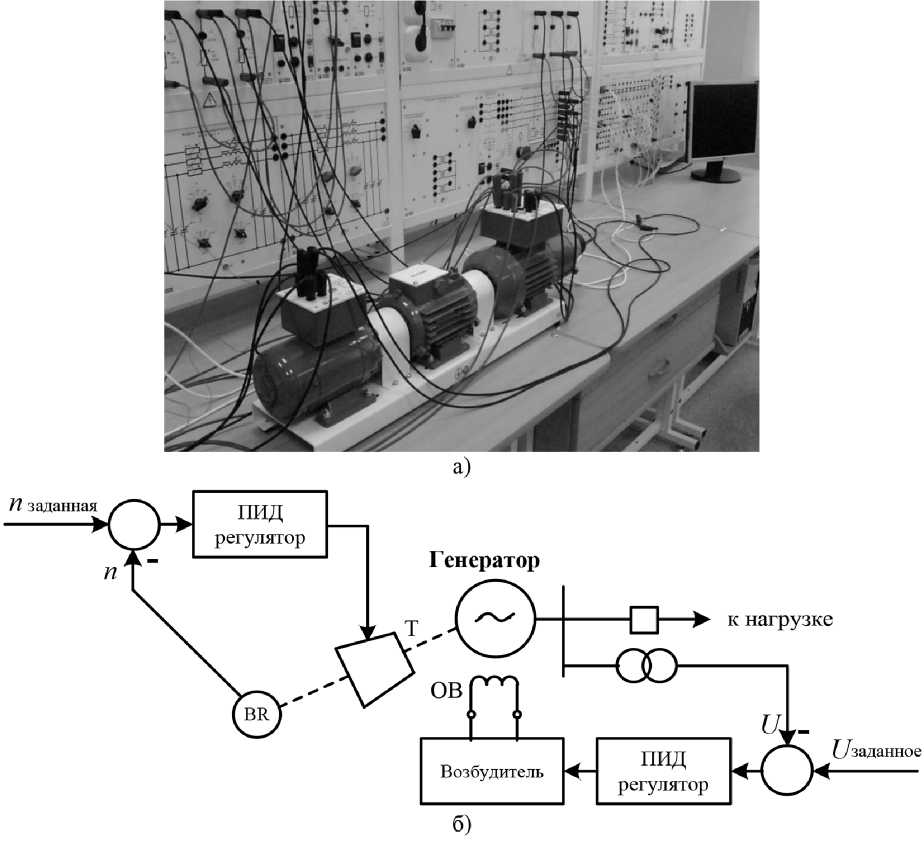
Рис. 6. Фото (а) и функциональная схема (б) физической модели установки РГ: Т – турбина; ОВ – обмотка возбуждения; BR – датчик угловых перемещений

Fig. 6. Photo (a) and functional diagram (б) of the physical model of the RG installation: T – turbine; ОВ – field winding; BR – angular displacement sensor

Рис. 7. Фото используемой платы ввода-вывода PCI 6024Е

Fig. 7. Photo of the used PCI 6024E input-output board

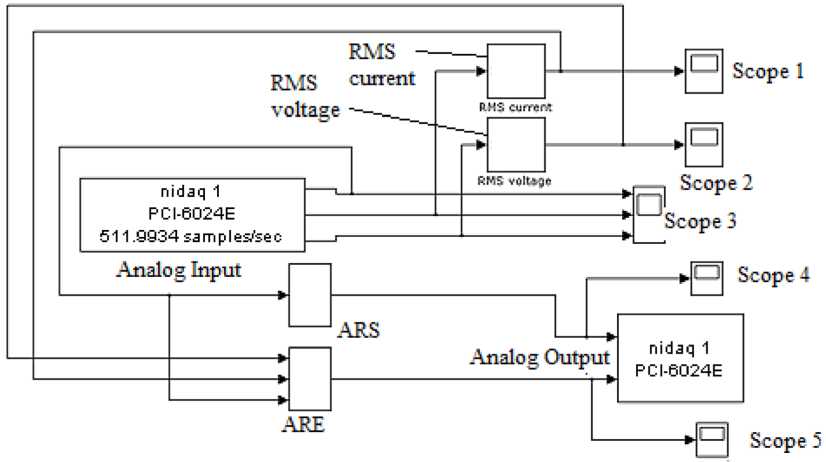
Рис. 8. Схема Simulink для управления физической моделью установки РГ

Fig. 8. Simulink scheme for controlling the physical model of the DG plant

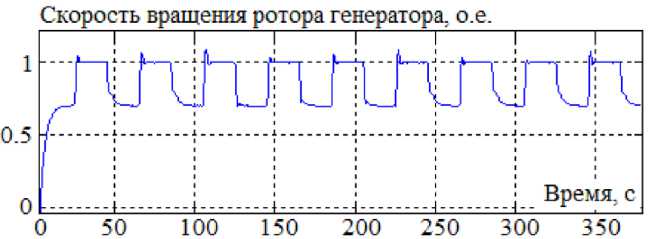
Рис. 9. Осциллограмма скорости вращения ротора генератора

Fig. 9. The oscillogram of the generator rotor speed

По полученным экспериментальным данным с помощью разработанной программы была построена и оптимизирована нечеткая модель регулирования скорости вращения ротора. Ее тестирование выполняли при случайных коэффициентах настройки регулятора (рис. 10). Результаты показали высокую точность (среднеквадратичное отклонение составило менее 0,008) и практическую пригодность разработанной программы для построения отдельных связей цифрового двойника установки РГ.

Таким образом, результаты исследований показали достаточно высокую эффективность использования нейронных сетей, системы нечеткого логического вывода и генетического алгоритма для построения цифровых моделей по экспериментальным данным . При этом применение генетического алгоритма позволяет оптимизировать параметры функций принадлежностей.

Заключение

Предложена структура цифрового двойника установки РГ, реализованной на основе синхронного генератора с нечетким блоком автонастройки АРВ и АРС, в виде иерархической модели, построенной с помощью экспериментальных данных.

Скорость вращения, о. е.

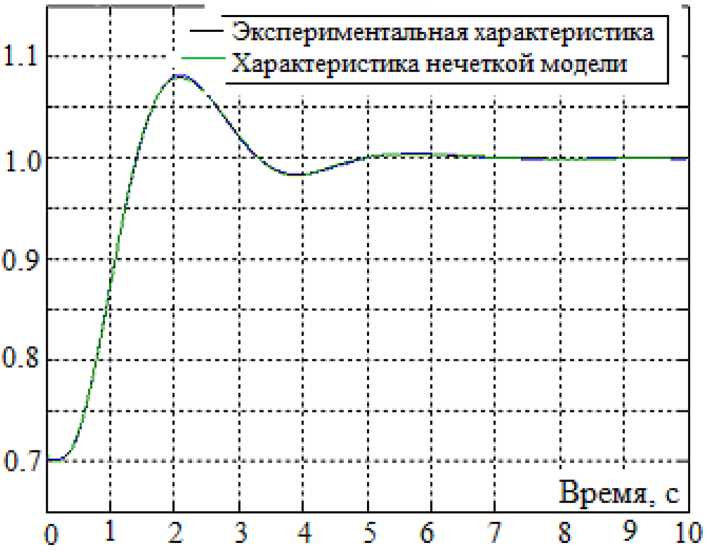
Рис. 10. Характеристики, полученные при тестировании нечеткой модели

Fig. 10. Characteristics obtained when testing a fuzzy model

На основе результатов расчета и моделирования можно сформулировать следующие выводы:

• –    представленные алгоритмы позволяют получать и оптимизировать функции принадлежностей терм-множеств и количество правил нечеткой модели цифрового двойника установки РГ, построенной на основе экспериментальных данных;

• –    предложенные алгоритмы могут быть использованы при проведении дальнейших исследований, направленных на промышленную реализацию цифровых двойников установок РГ, а также для решения задачи настройки автоматических регуляторов синхронных генераторов малой мощности.