Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова

На практике исследование и оценка устойчивости сложных динамических систем, содержащих линейные связи между процессами, были бы очень сложны. Декомпозиции этих систем на подсистемы с линейными связями упрощают исследование и оценку сложных систем. На основе метода векторной функции Ляпунова и принципа сравнения Матрасова построены системы сравнения с агрегирующей матрицей, а затем оценены устойчивость сложных систем через систему сравнения.

В работах [8–12] построены оценки векторной функции Ляпунова, система сравнения, условия устойчивости для непрерывных линейных систем, даны понятия и оценки, но конкретного алгоритма не разработано.

В настоящей статье построены подробные алгоритмы для получения системы сравнения и оценки условий устойчивости для непрерывных и дискретных объектов сложных систем. Эти алгоритмы являются основой анализа влияния линейных связей на устойчивость стационарных динамических систем и дальнейших исследований нелинейных и нестационарных динамических систем.

Декомпозиция непрерывных и дискретных систем

Системы состоят из множества подсистем, связанных между собой линейными связями. Непосредственное исследование таких систем очень сложно. Для упрощения процесса исследования разобьем исходную систему на подсистемы с соответствующими линейными связями, покажем процедуру децентрализации сложных систем на более простые подсистемы и дадим оценку на основе векторной функции Ляпунова. При этом построим новую систему сравнения, более простую, чем исходная, и на основе свойств этой системы определим свойства исходной системы.

В линейном случае поведение сложной динамической системы моделируется непрерывным и дискретным объектами:

непрерывные системы x = Ax + Bu, x(0) = x0;                                   (1a)

дискретные системы

x ( k + 1 ) = Ax ( k ) + Bu ( k ) , x ( 0 ) = x 0 ,                            (16)

где k - дискретное время; x e R n - вектор состояния системы; u e R m - вектор управляющих воздействий; A e R n ^x n , B e R n ^x m - матрицы параметров системы.

На основе структурной или формальной декомпозиции исходная система представляется в виде совокупности взаимодействующих подсистем:

непрерывная система	N xi = A i x i + E A jj x j + B i u i , j = 1, j * i x i ( 0 ) = x i 0 ,                                                             (2а) N h i = E A j X j , i = I’N ; j = 1, j * i
дискретная система	X i ( к + 1 ) = A i X i ( к ) +Е> х ( к ) + j = 1, j * i + B i u i ( к ) , x i ( 0 ) = x io ,                                        (26) h i ( X i ( к ) ) = e ax ( к ) , i = i; n , j = 1, j * i

Rn i - вектор состояния г-й подсистемы; h - вектор управляющих воздействий г-й подсистемы; Aj - матрица связей; Bi е RniXmi - матрица управлений i-й подсистемы,

NN

E n i = n , E m i = m .

ⁱ 1 Диагональные матрицы A, е R ^{n, x} n определяют диагональные подсистемы N_i , а слагаемые h_i (или h_i ( x i ( ^к ) ) ) в ^(2аМ^2б) – влияние подсистем с координатами x_j на координаты x_i и X_i подсистемы N_i (или влияние подсистем с координатами X j ( к ) на координаты x_i ( к ) и x_i ( к + 1 ) подсистемы N_i ).

Принцип сравнения для непрерывных и дискретных систем

Идея принципа сравнения при анализе сложных динамических систем существует давно. Описать основную идею принципа сравнения можно следующим образом. Вместо точной математической модели S сложной системы строится более простая математическая модель, которая может быть совершенно не похожа на точную, то есть не используется принцип подобия. В работах [1–3] конкретизирован принцип сравнения на основе теории векторной функций Ляпунова.

Рассмотрим принцип сравнения применительно к непрерывным и дискретным системам. Представим уравнения непрерывных и дискретных систем без воздействий и исследуем их на устойчивость:

непрерывные системы

X = F ( x ) ;                                             (3а)

дискретные системы x ( к +1) = F ( x ( к )).                                      (36)

Сформируем векторную функцию Ляпунова:

Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова непрерывные системы

V ⁽ x ) = ⁽ V 1 ⁽ x 1 ) , ^ , ^VN ⁽ x N ^{) ) ;}

дискретные системы

V ⁽ x ⁽ k ^{)) =} ( V 1 ⁽ x 1 ^{( k} ) ) , ^ , ^VN ⁽ x N ^{( k} ) ) ) ^.

С компонентами V i ( x i ) = x T H i x i и их полные производные (для непрерывных систем ), V ( x i ( k ) ) = x^T ( k ) H i x i ( k ) и разностные уравнения (для дискретных систем ) в силу исходной системы (3а)–(3б):

непрерывные системы т^(xi ) = [gradx.V^xi)] xi;                                 (4a)

дискретные системы

A V ( x i ( k ) ) = V ( x i ( k + 1 ) ) - V i ( x i ( k ) ) ,                              (46)

где H i = H T >  0 .

Эффективность подхода, основанного на принципе сравнения, связана с возможностью построения векторной функции f ( V ( x ) ) и f ( V ( x ( k ) ) ) такой, что выполняется неравенство:

непрерывные системы

V (x )< f (V (x));

дискретные системы

V (x (k + 1))< f (V (x (k ))).(56)

От неравенств (5а)–(5б) можно перейти к дифференциальным уравнениям систем сравнения:

непрерывные системы z^ = f (z);

дискретные системы z (x (k+1))=f (z (x (k))), где zeRN, z(0) = z0 - вектор состояния системы сравнения.

Для упрощения исследования устойчивости системы (3а)–(3б) необходимо провести исследование устойчивости системы сравнения (6а)–(6б).

Структура оценок производных функций Ляпунова

Пусть подсистема, соединенная с другими подсистемами посредством линейных связей, имеет следующий вид:

непрерывные системы

N

^ ^ i = Ai ^xi ⁺ ^ A jj^xj ⁺ B i u i ;                                    ⁽ 7a)

j=1, j * i дискретные системы

x i ( k + 1 ) = A i x i ( t ) + B i u i ( k )

N

⁺ S A ii x i ^{( k} )

N где i = 1, N, S j

N

S

j = ^1, j * i

A ij X j ( k ) - линейные связи подсистем.

^j = ^{1, j} * i           ^j = ^{1, j} * i

Для линейной стационарной системы (7а)-(7б) скалярные функции Ляпунова V i ( x i )

и Vi (xi (k)) диагональных подсистем выбираются в виде квадратичной формы: непрерывные системы дискретные системы

x i = A i x i +

N

S Ax + B i u i ;

^j = ^{1, j} * i

V i ( x i ( ^k ) ) = ^xT ( ^k ) H ix. ( ^k ) ,

(8a)

H T     n. x n.

i = H i g R i i - положительно определенная матрица как решение матричного уравнения Ляпунова [3]:

непрерывные системы

A T H i + H i a . + Q i = 0,                                (9a)

дискретные системы

A T H i A - H i + Q i = 0,                              (96)

где Q i = Q T > 0 g R ⁿ i ^x n i .

Вычислим полную производную V i ( x i ) и приращение A V i ( x i ( k ) ) в силу уравнения (7а)–(7б):

дифференциальные уравнения

V i ( x i ) = ( ^x T Hx ⁺ x T H i x i )

= x T A T H i x i + x T H i A i x, + 2 u T B T H i x i ;

разностные уравнения

^A V i ( ^x ( ^k ) ) = ( x T ( ^{k + 1} ) H i x i ( ^{k + 1} ) ^{- x}T ( ^k ) H i x i ( ^k ) ) ,

= x^T ( k ) A T H i A i x i ( k ) - x^T ( k ) H i x i ( k ) + 2 u^T ( k ) B^TH i A i x i ( k ) + u^T ( k ) B T H i B i u i ( k ) .

При экспоненциальной устойчивости нулевого решения изолированных подсистем (непрерывные) и автономных конечно-разностных уравнений (дискретные) допускается обращение в соответствии с результатами теоремы Н.Н. Красовского, и у каждой подсистемы существует скалярная функция Ляпунова:

непрерывные системы c2 ||xi 112 ^ Vi (xi) ^ c 2 i ||xi 112; Vci (xi )^ - c2 i I xi 112; | gradxVv. (xi )|| ^ c 4 i ||xi 112           (!°a)

дискретные системы

c2i llxi(k )| 12 - Vi (x(k))- c 2 i llxi(k )| 12;A Vi (x (k))- - c2 i llxi(k )| 12               (106)

Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова где cki >0, k = 1,2,3,4.

Неравенства (10а)–(10б) являются оценкой производных функций Ляпунова. От (10а)–(10б) можно построить неравенства (5а)–(5б).

Построение систем сравнения

Для непрерывных систем: построение элементов агрегированной системы. При внешних воздействиях вводится функция Ляпунова в виде v i ( x ) = ( V i ( x i )) ^ = ( x^T H i x , ) [2].

Для компонентов v , ( x ) векторной функции Ляпунова имеют в силу оценки Красовского:

c 1 i ll x i 1I <  v i <  c 2 i I x i I | >- ^Vi <  -n l x , 1| >- grad^x, 11 <  ц , || x i ||

(11a)

Параметры c li , з i , м i определяются следующим образом:

c i i = xT ( h , ) ; c 2 i = 4 ² ( h , ) ;

з    c²^ = ^X m ⁽ Q i ) ; м. =    = ^X M ⁽ H i ) .

' ² c 2 i 2 X 1 ( H i )    ' ² c 1 i 2 4 1 ( H i )

где Сц > 0, l = 1,2,3,4 ; X _m ( A ) , X M ( А ) - соответственно, минимальное и максимальное собственные числа матрицы А .

Вычисляя полную производную функции v i ( x i ) в силу уравнения (2а), определяющего поведение взаимосвязанных подсистем, имеем

/ „       Л            Л  I „ NI

• ( A — I 5V,   .      | | dv,          I ,

^Vi ⁽ x i ) = | д   , A i xi | + | д   , ^Bi u i |+   д   , / , Ai j x j .

(axi     ; (axi     ;  ^аx, j =^tij

В силу первого и третьего неравенства Н.Н. Красовского оценки компонентов V i ( x i ) производной функции Ляпунова примут вид

Vi(x,)<-73rv,(xi)+^-XM/1 (bTb,)|ui|+-^4- £ XM’(ATA,j)Vj(x)

² c 2 i              2 c l i                           2 c l j c 1 i j = 1, j ^ i

Векторная функция Ляпунова v ( x ) = ( V 1 ( x 1 ) , ^ , v_n ( x_N ) ) с компонентами в виде скалярных функций, последнее неравенство (11а) можно представить в векторной форме:

V ( x ) < Wv ( x ) + Г| и |,

(13a)

(14a)

N где 1g R - агрегирующая матрица.

Тогда система сравнения с агрегирующей матрицей имеет вид z = Wz + Ги, z (0 ) = z 0

где z e R N , W e R N ^x N - вектор состояния агрегированной системы. Из (12а) получены элементы матриц W и векторов Г:

W = { W j i N =1

wi

2m ( Qi ) w,, =---——

22m ( H )

, = 2m ( H i ) A M² ( AAL ) jj" A m² ( H i ) 2 m² ( H j )

(15а)

Г = diag { Y i } ^f ,

Y i = [ 2m ( H i ) 2 M ^/2 ( B^T B i ) ] 2 „ ;^1/2 ( H i ).

Для дискретных систем: построение элементов агрегированной системы. Функцию Ляпунова в виде квадратичной формы

Vi (x (к )) =xT (к) Hixi (к)

удовлетворяет требованиям (10б) с параметрами c 1 i = 2 m ^/2 ( H i ) , c 2 i = 2 M ² ( H i ) . Для определения c 3 i вычислим конечную разность функции Ляпунова V i ( x i ( k ) ) вдоль траекторий подсистем (7б), замкнутых децентрализованными регуляторами:

АVi (xi (k)) = Vi (xi (k ' 1)) Vi (xi (k))

= x^T ( k + 1 ) H i x i ( k + 1 ) - x T ( k ) H i x i ( k )

= ^xT ( ^k ) ( A T H i A i ) x i ( ^k ) ^{- x}T ( ^k ) H i x i ( ^k )

+ u^T ( k ) B T H i B i U ( k ) + £ x T ( k ) A T H i A j x j ( k )

j = ^1, j * i

+ 2 x^T ( k ) A T H. £ A j x j ( k ) + 2 x^T ( k ) A T HM ( k ) j = 1, j * i

N

^{+ 2} u i ^{T ( k} ) B iT H i У A ij x j ^{( k} ) .

j = 1, j * i

Отсюда с учетом оценок, справедливых для матриц А , Q и векторов a , b с согласованными размерностями

2 a^T А ^T Q b <  a^T А ^T А a + b^T Q ^T Q b

У 2aTАTQ,b, < NaTАTАa + У bTQ,TQ,b,. ii                         i i ii i=1                                                i=1

Тогда функции V i ( x i ( k ) ) удовлетворяют конечно-разностным неравенствам:

V i ( ^xi ^{( k + 1 )}) < x i ^{T ( k} ) A T ( ^NEn, ⁺ H i ) ^Ai^xi ^{( k} )

N

+ u T ( k ) B T ( H i + NH² ) B.U i ( k ) + У x T ( k ) A TT ( NE ^ + H i + H ² ) A ^ x j ( k ) .

j = 1, j * i

Перейдя в последнем неравенстве к евклидовой норме векторов xi,xj,ui и используя известные экстремальные свойства отношения Релея max((x,Dx^/(x,x)) = 2M (D), имеем

Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова

V ( x i ( k + 1 ) ) ^ A M [ A T ( NE n, ⁺ H i ) A i ]| x i ( k )| 12

+ am [ B T ( H i + NH 2 ) B i ]| U i ( k )|Г + £ am [ A T ( NE n, + H + H ) A i, ]| x , ( k )|f;

j=1, j * i получаем мажоранту для функции Ляпунова:

am ^[ A T ( NE n + H i ) A i 1

) B. ]l U i ( k ) r

^[ , ,_uX     ^] V ( X i ( k ) ) + am [ B T ( H i + NH

Am (Hi )                       L

+ £ A ^{M [} A T ⁽ NE n i Z H ; ^{+ H} 2 ) ^{A ]} V , ( x , ( k ) ) .

i = 1, j * i              A m ^{( H}j )

Также при внешних воздействиях вводится функция Ляпунова в виде [2]

vi ( X ( k )) = ( Vi( xi ( k ))) / =( xT ( k ) Hixi ( k )) / .

В силу последнего неравенства для функции v i ( x ( k + 1 ) ) имеет место следующая оценка (13б):

A M ² [ A T ( NE n + H i ) A i ] v i ⁽ x i ^{( k + 1 ))} ^---------- p/2                 v i ⁽ x i ^{( k )) +}

Am (Hi )

г                1         N AMT ^[ A T, ( NE n + H i + H i ² ) A i, ¹

+ A M ^/2 [ B T ( H i + NH 2 ) B i ] U i ( k ) + £ ---- ^{[   1} /'     ----- v , ( x , ( k ) ) .

j = 1, j * i              A m ( ^H, )

В силу векторной функции Ляпунова

v(x(k)) = (v1 (x1 (k)),^,vN (xN (k)))T с компонентами в виде скалярных функций последнее неравенство (13б) можно представить в векторной форме:

v ( x ( k +1)) < Wv ( x ( k )) + Ги ( k ), где ГеRN, WeRNxN - агрегирующая матрица.

Система сравнения с агрегирующей матрицей имеет вид z ( x ( k + 1 ) ) = Wz ( x ( k ) ) + Г и ( k ) , z ( x ( 0 ) ) = z ₀, где z e R ^N - вектор состояния агрегированной системы.

Из (13б) получены элементы матриц W и векторов G:

w ii

(   ) N

W = ^{ w ij ^} 1 = ^

W- = wij

_ ^M² [ A T ( NE n+ H i ) a , ]

i =       Ai/^TH^)

A M [ A TT ( NE n i + H i + H 2 ) A j ] A 1/ ² ( H j )

(15б)

Г = diag { у, } f ,

Y i = A M / ² [ B T ( H i + NH 2 ) B i ] , i = 1 N .

Условия устойчивости агрегированной модели

Для упрощения исследования устойчивости исходной сложной системы проведем исследования устойчивости системы сравнения, которая имеет меньшую размерность. Устойчивость системы сравнения можно легко проверить на основе применения критериев Гурвица.

Системы сравнения (14а)–(14б) имеют агрегатные матрицы W с недиагональными элементами будут неотрицательными ( w ij >  0 ) , если матрица W - матрица типа M (матрица Метцлера). Агрегатные матрицы W с отрицательными диагональными и неотрицательными недиагональными элементами обязательны для устойчивости, но этого недостаточно: требуется также соблюдение условий квазидоминирования диагонали. Для синтеза управляющих законов и устройств следует пользоваться условиями Севастьянова – Котелянского [3].

М-матрица А размерности N х N устойчива в том и только в том случае, если все ее четные последовательные главные миноры положительны, а нечетные – отрицательны:

( - 1 ) k

w 11

w 1 k

> 0, k = 1, N .

w k 1

w kk

Алгоритм построения системы сравнения

По результатам приведенного выше анализа можно предложить алгоритм построения системы сравнения.

Шаг 1. Построить подсистему, соединенную с другими подсистемами посредством линейных связей:

непрерывные системы дискретные системы

N x^i = Aixi+ ^ Aijxj+Biui;

j = 1, ^j * i

N xi (k + 1) = AX (k)+ ^ Aijxj (k) + Biui (k). j=1 j * i

Шаг 2. Построить уравнения Риккати и решить уравнения: непрерывные системы

A T H + HA i + Q i = 0;

Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова дискретные системы

A T HA - H i + Q i = 0.

Из этого шага нахождение матриц H_i .

Шаг 3. Вычислить параметры c i , з i , м i оценки векторной функции Ляпунова, i = 1, N : непрерывные системы

С 1 i = A m² ( H i ) ; c 2 i = ^ M ² ( H i ) ;

c. = c ² = ^A m ⁽ Q^ . - _= A = ^ M ⁽ H^ .

² c 2 i 2 A A ( H )        ² c _{X i} 2 ^ ( H i )

оценки векторной функции Ляпунова c1 ЖII- vi - c2<||xi||; vi --3 <||xi||; gradxv^|-Ax|;

дискретные системы

Оценки векторной функции Ляпунова c1 i Ixi (k)hvi (x(k))- c2i Ixi (k); c 1 i = Am/2 (Hi), c2i = AM/2 (Hi);

vi

A M [ A^T ( NE n_+ H ) a ] x i ⁽ k ⁺ O)  --------- _; 1/2/^ x -------^] vi ⁽ x i ^{( k} ) ) ⁺

^A m ⁽ H i )

+ A M [ B i ( H i +

^N aM Г a T ne„ + h, + h 2) A 1

NHi)B.1 u+ Z M [ ( ,i;2f„      i) j]Vj (Xj (k))• j=1, j ^ i            Am ( Hj )

Шаг 4. Построение системы сравнения с агрегирующей матрицей: непрерывные системы z = Wz + Ги, z(0) = z0;

A miQ^l

W = { W ij I f =]

ii     2Am ( Hi), wi

= Am ( H i ) A M ( A T A ) i '" AA ( H i ) AA ( H j ) ,

A = diag { Y i } ^f ,

Y i =[ ^A m ( H i ) A M ( B T B ) ^{1 A}A/ ( H i ) ; дискретные системы

z ( x ( k + 1 ) ) = Wz ( x ( k ) ) + Г и ( k ) , z ( x ( 0 ) ) = z 0 ;

W--ii

N

W =^{ w j ^} , =^

W-- = wij

_ A M ^/2 [ A T ( NE n+ H i ) A i ] i =       A n H")      ’

AM² [ A T ( NE n+ H i + H 2 ) A j ]

Am/2 (Hj)           ,

г = diag { Y i , Y i = X / [ B T ( H i + NH 2 ) B i ] .

Шаг 5. Условия устойчивости системы сравнения. Вычислены условия Севастьянова – Котелянского:

(-1)k

w 11

w 1 k

: >  0, k = 1 N .

w k 1

w kk

Применение алгоритма для анализа устойчивости ЭЭО

В линеаризованной форме исходные уравнения электромеханических процессов i- й ЭС имеют вид [5]

pi ^— H i = T ai ® ⁷ i ⁺ T yi ® i ⁺

+ L Pij (t, — Tj), j=1, j * i

Trnp i + P i = q i ,                                         ⁽¹⁷⁾

^Tci^q i ⁺ q i =^- km.®. ⁺ °" i ,

^TMi< j i + ^ i = u i , где T i , ® i , H i , ^ i , Pi , q i , u i — отклонения, соответственно, углов, частот, нагрузки, сигналов ре-гуляторов,мощностей,перетоковполиниямиуправлений i- йЭ С; T_ai , T yi , T _{n i} , T ci , T _{M i} , k ® i , p ij - параметры ЭС.

Система уравнений электромеханических процессов энергнообъединения с учетом регуляторов может быть представлена в форме Коши:

T i = ® ,

1 ⁿ                   T yi       1

-

0)' =-T~ L ^ij (Ti-Tj)-®i +  2"Pi ai j=1,i*j                      Tai         Tai

2 ^ ^H i , T ai

I p i =

^-~ ^p i ⁺ ™q i , T Ïi     T Ïi

• _  k®,       11

q i =-v ®i- ~qi +—^i, Tci      Tci

I

7 i

----CTi +

T Èi     T Èi

Пусть векторы состояний x = [t,®,p,q,^]T состоят из физических координат ЭЭО

вектора управлений U = [ u , h ] ^T . Эти координаты определяются следующим образом:

T = ( T 1 , ^ , T „ ) , ® = ( ® 1 , ^ , ® _п ) ,

P = ( P 1 P- , P n ) , q = ( q 1 , ^ , q n ) , ^ = ( o "1 ^, ^ ^, y « ) , u = ⁽ u 1 , ™ , u n ) , ^H = ^{( H} 1 , ™ , ^H n ) .

Тогда уравнения электромеханических процессов (17), (18) можно записать в форме Коши:

Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова

X = Ax + Bu , x ( 0 ) = x ₀,

где A = ( A lm ) B = ( B rs ) - блочные матрицы, причем l , r , m = 1,2,3,4,5, s = 1,2 , а клетки A lm , B rs имеют размер ( n x n ).

Декомпозиция моделей (19) по форме (2), и уравнения ЭЭО имеют вид где

	0 n - A Z P j ai j = 1, j * i	1 T . - yi 2 Tai
A =	0	0
		kv
	0	toi -
		т. ci
	0	0
	-

xi=\.,

to i , p i , 9 i ,t ^ i ]

T

A i x

n + Z

A iij x j + Bi ( u i

T , M i )

,

(20)

j = 1, j *

0

0

0

1 2 T ai 1 — T Ïi 0 0

0 1 T Ïi 1 — T ci 0     -

0 0 1 T. ci 1 — TMi _

A j =

Г 0 P ij T2 0 j 0 0

1 0 0 0 0

0 0 0 0 0

0 0 0 0 0

0 " 0 0 0 0

, Bi =

Г 0 0 0 - T Ei

0 " - 2- Ta 2 i 0 0 0 _

■

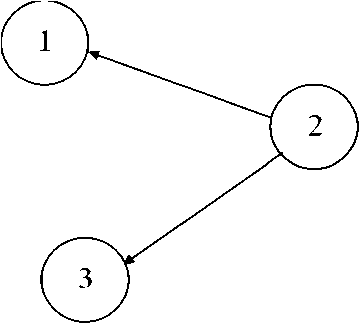
Рисунок 1. Схема исследуемого энергообъединения

Таблица

Параметры энергосистемы

i	T. ai	T . yi	T Ïi	T. ci	k to i	P ij
1	0,02	0,027	1,5	0,5	0,017	0,02
2	0,017	0,025	1,5	0,5	0,032	0
3	0,02	0,025	1,5	0,5	0,016	0,04

С помощью программы МАТЛАБ исследованы устойчивости ЭЭО. Вычислены параметры для оценок векторной функции Ляпунова:

c 1 = ( 0,0197 0,0168 0,0197 ) ; c 2 = ( 1,4704 1,4695 1,4701 ) ;

c 3 = ( 1 1 1 ) ; c 4 = ( 2,0794 2,0782 2,0790 ) ;

П = ( 25,3441 29,7852 25,3187 ) ; ц = ( 109,5821 128,6328 109,4275 ) .

Тогда для ЭС-1

0,0197| (xj |< v1 ( x1 )< 1,4704| Х1Ц, p1 (x 1)< -25,3441||x 111; \\grddvv1 (x1 )||< 109,5821]|xi||;

для ЭС-2

0,0168] x 211< v 2 ( x 2 )< 1,4695] x 2||, v2 ( x 2 ) < -29,7852] X 211; |gradx 2 v 2 ( x 2 )|| < 128,6328] |x 21|;

для ЭС-3

0,0197] | x ₃| |< v 3 ( x 3 ) < 1,4701|| x ₃|| ,

V 3 ( x 3 ) < — 25,3187]| x 31| ; \gradd v 3 v 3 ( x 3 )|| <  109,4275 1| x 31|-

Получены элементы агрегированной матрицы

- 0,2313    383587,2441       0

W = 383942,7791    - 0,2316

766346,5191

0        766861,0007    - 0,2314

Условия устойчивости Севастьянова – Котелянского имеют вид

( - 1 ) 1 det| w _n| = 0,2313 >0,

( - 1 ) 2 det

w ₁₁   w ₁₂

w 21   w 22

- 0,2313    383587,2441

= 383942,7791    - 0,2316

= - 1,4728e +11 <  0;

( - 1 ) ³ det J W | = 1,6999e + 11>0.

Таким образом, условия Севастьянова – Котелянского не выполнены , поэтому ЭЭО из трех ЭС с двумя линиями является неустойчивым.

Для наглядности построим переходные процессы для каждой координаты системы в каждом ЭС. На графиках показаны векторы состояния в каждом ЭС (см. Рисунки 2–4).

Из графиков видно, что 4 параметра ® , p , q , с т вектора состояния асимптотически к начальному равновесию, первый параметр ф вектора состояния асимптотически к значению 0,3. Интуитивно видно, что система устойчива в состоянии, отличном от начального равновесия.

Связи между ЭС представлены параметром ф . Из графиков и агрегированной матрицы видно, что значения недиагональных матриц гораздо больше, чем значения диагональ-

Алгоритмы построения системы сравнения и оценки векторной функции Ляпунова ных матриц (Aij » Aii) . Это

означает, что влияние связей на устойчивость системы до- вольно сильно.

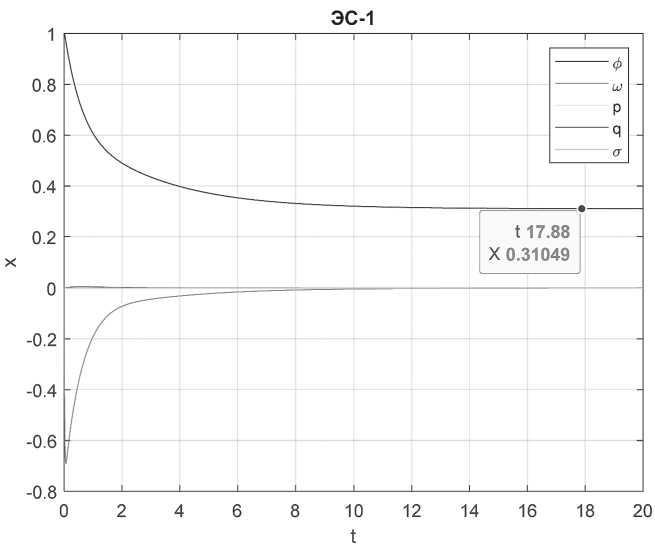
Рисунок 2. Переходные процессы для ЭС-1

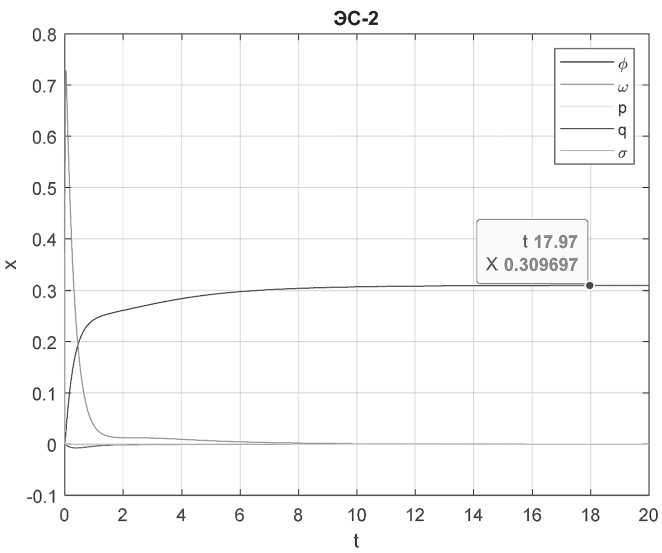
Рисунок 3. Переходные процессы для ЭС-2

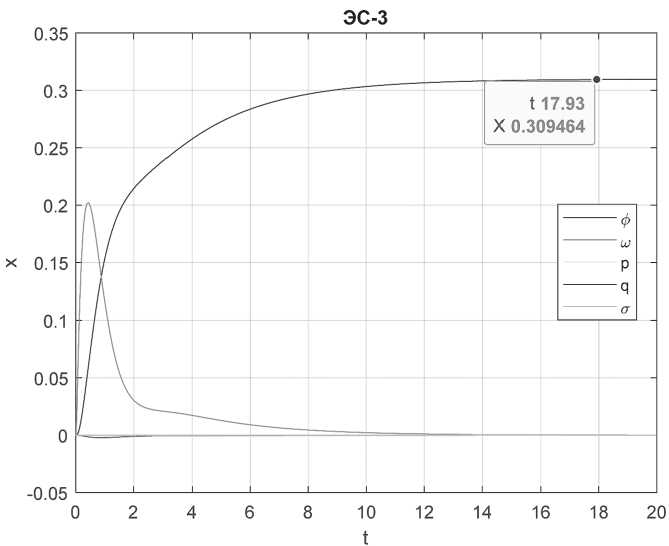
Рисунок 4. Переходные процессы для ЭС-3

Заключение

Алгоритмы поддерживают вычисление векторной функции Ляпунова и построение системы сравнения для непрерывных и дискретных объектов сложных динамических систем. Это основа для оценки устойчивости сложной системы и влияния линейных связей на устойчивость системы.