Алгоритмы расчета комплексных показателей в динамических структурах представления данных

Проблема разрыва между научными методами представления (описания) объектов реального мира и хранения информации о них в информационных системах существует уже давно и в настоящее время не нашла своего удовлетворительного решения. Так, самые передовые на сегодняшний день системы управления базами данных (СУБД), позволяющие сохранять информацию в виде объектов [1; 2] (объектно ориентированный подход [3]) или в виде глобалов [1] (иерархическое представление информации в виде дерева) – не могут охватить и доли всего многообразия представления информации современными научными методами [4]. Такой разрыв в значительной степени тормозит развитие прикладных наук и инженерии в области информационных технологий.

В связи с этим одним из существенных ограничений создания информационных систем является общепринятый способ хранения данных на базе статических структур (т. е. для описания объектов предметной области с целью хранения информации о них в базе данных заранее создаётся структура хранения данных). Это приводит к тому, что такая структура должна быть создана проектировщиком информационной системы еще на этапе ее проектирования и она (эта структура) не может изменяться в течение создания этой системы и ее эксплуатации. Стоит ли говорить, к каким затратам приводят изменения в структуре хранения информации на этапе создания информационной системы и ее эксплуатации… Очевидно, что если такие изменения возможны, то только в незначительной части этой структуры, иначе стоимость переработки может совпадать со стоимостью создания самой информационной системы и даже превышать её.

Любые попытки создания динамических структур хранения данных приводят к появлению задачи трансформации этих данных в один из существующих способов их хранения в СУБД (реляционный, объектный или иерархический). Ни один из перечисленных способов не способен работать напрямую с динамическими структурами. Зачастую такие задачи решаются индивидуально по мере их возникновения. В результате отсутствуют какие-либо общие подходы для решения этих задач, а реализованные в некоторых программных продуктах в виде отдельных модулей подобные задачи, представляют собой коммерческую тайну. Таким образом, существует научная задача описания динамических структур данных, обработки информации в этих структурах и хранение её в СУБД, а также частная задача расчета комплексных показателей на множестве фактографических данных в динамической структуре, решение которой и предлагается в данной статье.

Представление фактографических данных на трехдольном графе. Для описания динамической структуры данных предлагается выделять следующие категории информации [5]:

• –    показатели – количественные характеристики объектов;

• –    классификаторы – структурообразующие данные, состоящие из взаимосвязанных классов и их экземпляров (объектов);

• –    фактографические данные – значения показателей в отношении одного или нескольких классификаторов.

Для представления каждой категории информации будем использовать соответствующее графовое описание.

Граф показателей состоит из двух частей, одна из которых представляет собой дерево (рис. 1), содержащее вершины-категории (классификация показателей), а другая – простой граф с произвольным числом долей этого графа, вершины которого представляют собой показатели.

Категории                      Показатели

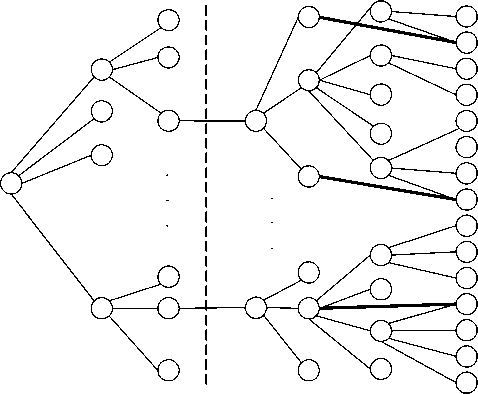
Рис. 1. Граф показателей

В части категорий ребра показывают (слева направо) разбиение категорий на подкатегории, а в части показателей ребра показывают (слева направо) разбиение агрегированных показателей на более частные до элементарных показателей (неделимых). Агрегированные показатели могут состоять не только из показателей предыдущего уровня ( k ), но и из показателей следующего уровня ( k + 1), через уровень ( k + 2) и т. д.

Рассмотрим граф классификаторов (рис. 2). Граф делится на три уровня, каждый из которых несет собственную смысловую нагрузку. Так, уровень категорий пред- назначен для разбиения классификаторов на укрупненные категории, т. е. описания структуры классификационного дерева. На уровне классификаторов представлено множество вершин (классификаторов) с ребрами между уровнем категорий, показывающими принадлежность каждого классификатора к какой-либо категории, и ребрами между вершинами классификаторов, показывающих связи между ними, а сама вершина характеризуется не только ее наименованием, но и набором атрибутов.

Уровень значений классификаторов аналогично предыдущему уровню содержит множество вершин, каждая их которых имеет одно обязательное ребро, показывающее принадлежность значения к какому-либо классификатору, и несколько необязательных ребер, показывающих зависимость между значениями разных классификаторов. Вершины данного уровня также характеризуются наименованием и значениями атрибутов, соответствующих вершинам в уровне классификаторов, с которыми они связаны рёбрами.

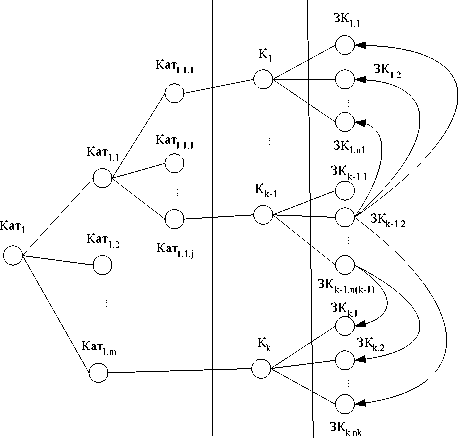
Уровень категорий                Уровень          Уровень значений классификаторов             классификаторов       классификаторов

Рис. 2. Граф классификаторов:

Кат – категория классификаторов; К – классификатор;

ЗК – значение классификатора

Рассмотрим в качестве примера организационную структуру некоторой организации (рис. 3) и выделим две сущности в этом примере – управление и отдел. Проведем аналогию графового представления структуры классификаторов (рис. 3, а ) с другими способами представления данных, например, с объектным (рис. 3, б ).

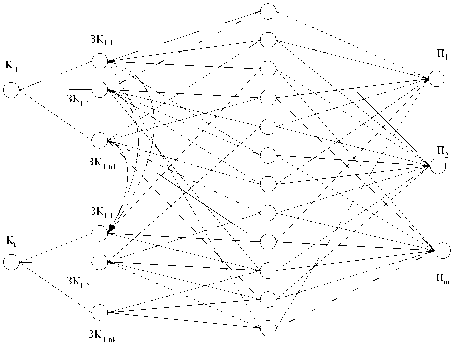
Фактографические данные представляют собой граф со множеством вершин, не имеющих ребер между собой, но имеющих ребра с вершинами графов классификаторов и показателей (рис. 4). Вершины фактографических данных представляют собой числа, которые являются количественными характеристиками одного или нескольких показателей в отношении с одним или несколькими классификаторами. Например, для показателя «заработная плата» и значения классификатора «отдел социальной работы», значение фактографического данного может равняться X рублей в год.

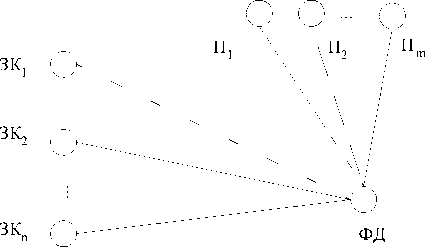
Рис. 4. Фрагмент графа фактографических данных: ЗК – значение классификатора; П – показатель;

ФД – фактографическое данное

Таким образом, вершины фактографических данных, соединяясь с вершинами графов классификаторов и показателей, образуют граф со сложными взаимосвязями (рис. 5).

Для проведения аналитических операций над фактографическими данными с целью вычисления комплексных показателей будут использоваться не все вершины и рёбра графа. Например, для расчета суммарной годовой заработной платы в организационной единице «управление корпоративной политики» нужно просуммировать

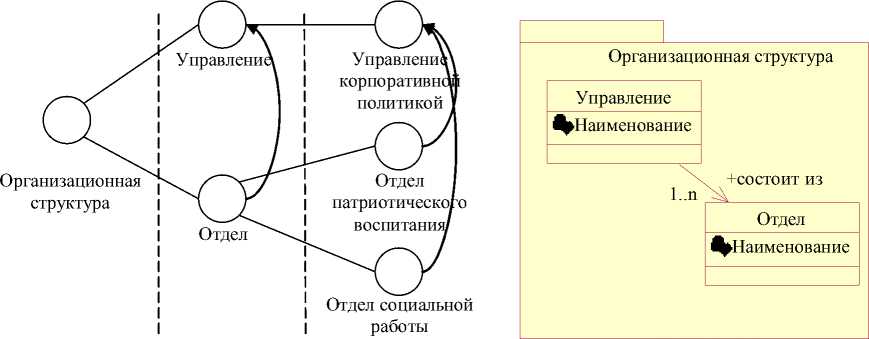
аб

Рис. 3. Примеры представления структур: а – графовый вид; б – объектный вид

значения фактографических данных, у которых есть связи с вершинами, представляющими отделы этого управления, и вершиной показателя «заработная плата». Таким образом, из всего графа, представленного на рис. 5, будут использоваться только вершины фактографических данных и связанные с ними вершины графов классификаторов и показателей. Кроме того, если в качестве исходных данных для алгоритма вычисления комплексного показателя будут использоваться множество вершин значений классификаторов и множество вершин показателей, для которых нужно произвести вычисление, то рёбра между вершинами значений классификаторов будут не нужны. Поэтому, учитывая все вышесказанное, упростим граф фактографических данных (см. рис. 5) до трехдольного графа (рис. 6), который представляет собой три множества вершин ( X ₁ , X ₂ и X ₃ ), в каждом из которых вершины не имеют рёбер между собой, но имеют рёбра между вершинами соседних множеств [6].

ФД

Рис. 5. Граф фактографических данных: К – классификатор; ЗК – значение классификатора; П – показатель; ФД – фактографическое данное

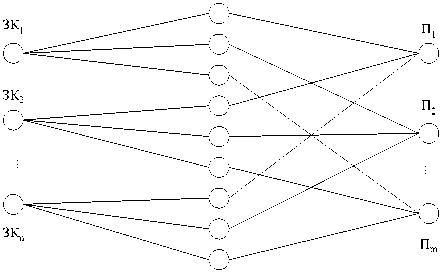
X ₁

X ₂

X ₃

Рис. 6. Трехдольный граф фактографических данных: ЗК – значение классификатора; П – показатель; X – множество вершин трехдольного графа

Тр ехдольный граф является частным случаем N-дольного графа (рис. 7), который обладает собствен- ными свойствами отличительными от простого графа, для которого уже существуют некоторые алгоритмы его обхода [7].

Такие алгоритмы плохо работают на N-дольных графах, поскольку они ориентированы на достижение других целей (нахождение кратчайшего пути, поиск определенных значений и др.), а не решения задачи отбора вершин в одной из долей с заданными условиями через подмножества вершин в соседних долях. Именно с такими свойствами требуется алгоритм обхода графа для расчета комплексных показателей. В данной работе предлагаются алгоритмы обхода N-дольного графа с целью поиска вершин в одной доле, имеющих полное множество ребер ¹ с заданными через условия поиска подмножествами вершин в соседних долях графа.

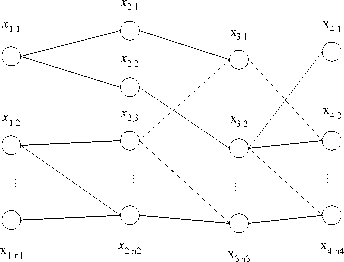
X ₁                 X ₂               X ₃             X ₄

Рис. 7. N-дольный граф: x – вершина графа; X – множество вершин трехдольного графа

X m

Алгоритмы поиска на N-дольном графе. Для осуществления поиска вершин в одной доле N-дольного графа необходимо определить два подмножества вершин X_k - 1 и X k + 1 , объединённых в множество условий поиска U_k, где k – номер доли, в которой будет выполняться поиск. При осуществлении поиска вершин в k -й доле будет сформировано подмножество X_k ^' , в которое будут отобраны вершины, имеющие полное множество ребер с подмножествами из условий поиска:

U k = X k - 1 и X k + 1 . (1)

Для каждой вершины x_k i е X_k будет выполняться следующее условие:

(Г( х^ ) о X k - 1 ) и ( Г ( х_к . ) о X k + 1 ) = X k - I и X k + i , (2) где Г( x_{k , i} ) – множество всех вершин, имеющих рёбра с вершиной x_{k , i} .

Ниже описаны два новых алгоритма поиска на N-дольном графе: «обход окрестностей одной вершины» и «пометка вершин».

Обход окрестностей одной вершины

• 1.    Отобрать все вершины из множества X_k , которые имеют рёбра с одним из элементов из множества U_k и поместить их в множество X_k ^' .

• 2.    Проверить каждую вершину x_k i е X_k, имеет ли она полное множество ребер с вершинами множества U_k . Если условие не выполняется, то вершина x_{k , i} удаляется из множества X_k ^' .

Анализ данного алгоритма позволил выявить зависимость количества переходов С , необходимых для осуществления поиска, от условий поиска:

C = Ё (| Г ( x k , i )| — 1 ) , (3)

i = 1

где Г ( x_{k , i} ) – количество вершин, связанных с элементом x_k ^' _{, i} .

Пометка вершин

• 1.    Выбрать вершину u_{k , i} из множества U_k . Ввести множество меток M , размерность которого равна X_k , и каждому элементу этого множества присвоить «0». i = 1.

• 2.    Для вершины u найти множество Г ( u_ki ) с X_k . Для каждого x_kj е X_k, для которого выполняется условие x_k j е Г ( u_ki ), соответствующей метке m j е M увеличить значение на «1».

• 3.    i = i + 1. Если i = n , перейти к следующему шагу. Иначе перейти к шагу 2.

• 4.    Найти вершину в множестве U_k с наименьшим количеством рёбер и поместить связанные с ней вершины из X_k в множество X_k ^' .

• 5.    В результирующее множество X _r ^' _es из множества X_k ^' отобрать вершины, имеющие полное множество рёбер с вершинами из множества U_k : X Г_С5 = { V x_k , i е X_k I m i = Uk } .

Определим для данного алгоритма зависимость количества переходов С , необходимых для осуществления поиска, от условий поиска:

n

C = E| Г ⁽ u^^{е X}A ^{+ min(} A ), (4) i = 1

где A = {| Г ( u_k , i ) е X_k |, i = 1, n } .

Анализ формул (3), (4) показал, что при небольшом количестве условий поиска (от 1 до 4) эффективнее (с точки зрения количества переходов между вершинами графа) работает алгоритм «пометка вершин», а при увеличении условий поиска эффективнее работает алгоритм «обход окрестностей одной вершины».

Алгоритмы вычисления комплексных показателей. Комплексный показатель вычисляется на множестве фактографических данных X ₂ трехдольного графа G₃ (рис. 6) путем выделения подмножества X ₂ с X ₂ , удовлетворяющего условиям U ₂ (1), и выполнения операций над этим подмножеством. Таким образом, функция вычисления комплексного показателя (КП) представляет собой алгоритмическую функцию поиска на трехдольном графе с заданными условиями и аналитическую функцию преобразования над полученным множеством:

КП = F ( G₃, U ₂ ). (5)

Рассмотрим пример вычисления комплексного показателя с применением новых алгоритмов поиска на N-дольных графах. Допустим, на трехдольном графе фактографических данных (рис. 8) требуется вычислить количество выпускников в 2007 г. по специальности «токарь». В таблице приведено описание вершин графа для данного примера.

Перед началом поиска в соответствии с примером зададим множество условий (1):

^U 2     { x 1,3 , x 1,5 ^{} u {} x 3,1 ^}    { x 1,3 , x 1,4 , x 3,1 ^} .

x1.1

x1.2

x1.3

x1.4

x1.5

x1.6

x1.7

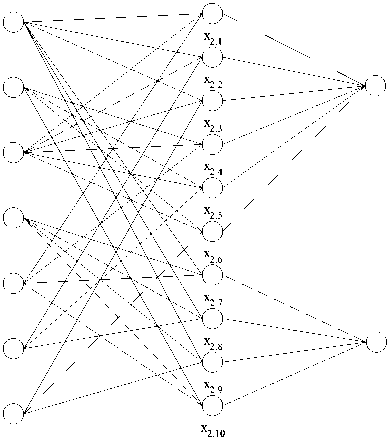
x3.1

x3.2

X ₁                          X ₂                       X ₃

Рис. 8. Пример фактографических данных о выпуске специалистов: x – вершина графа; X – множество вершин трехдольного графа

Применение алгоритма «Обход окрестностей одной вершины»:

• 1.    Отобрать все вершины из множества X ₂ , которые имеют рёбра с вершиной x _1,3 из множества U ₂ , и поместить их в множество X ^' = { x , x , x , x , x , x }.

• 2.    Проверить каждую вершину x ₂ i е X ₂ , имеет ли она полное множество ребер с вершинами множества U ₂ . Если условие не выполняется, то вершина x _{2, i} удаляется из множества X ₂ ^' . В результате в множестве X ₂ ^' остаются следующие элементы { x _2,1 , x _2,3 }.

2        2,1    2,2 '2,3    2,4'2,5    2,6

Значения элементов множества X ₂ ^' берем из таблицы. Для вычисления комплексного показателя «количество выпущенных специалистов в 2007 г.» выполним операцию суммирования над элементами получившегося подмножества и получим искомое значение – 15.

Применение алгоритма «Пометка вершин»:

• 1.    i = 1. Выбрать вершину u _{2, i} из множества U₂ : ( u₂₁ = x 1 ₃ ). Ввести множество меток M , размерность которого равна X ₂1 = 10 и каждому элементу этого множества присвоить «0».

• 2.    Для вершины u ₂ i найти множество Г( u ₂ i ) с X ₂ для V i . Для каждого x ₂, j е X ₂ , для которого выполняется условие x₂ j е Г( u ₂ i ), соответствующей метке m j е M увеличить значение на «1».

• 3.    Найти вершину в множестве U ₂ с наименьшим количеством рёбер в нашем случае x _{1 5} и поместить свя-

• занные с ней вершины из X2 в множество X2' ={x2,1, x2,3, x2,10}.

• 4.    В результирующее множество X _r ^' _es из множества X ₂ ^' отобрать вершины, имеющие полное множество рёбер с вершинами из множества U ₂ : X res = ^{{ V} x 2,i ^G X 2 I ml = ^U 2 ^} ={ X 21 , X 2,3 }.

i = 1: u 2,1 = x 1,3 , Г⁽ u 2,1 ) ={ x _{2 1} , x ₂₂ , x ₂₃ , x ₂₄ , x ₂₅ , x 26 }, M = {1, 1, 1, 1, 1, 1, 0, 0, 0, 0};

i = 2: u 2,2 = ^x 1,5 , ^{Г( u} 2,2 ) =^{{ x} ₂ 1 , ^x ₂₃ , ^x _{2 10} ^}, M = ^{2, 1, ², 1, 1, 1, 0, 0, 0, 1};

i = 3: u 2,3 = ^x 3,1 , Г⁽ u 2,3 )={ x _{2 1} , x ₂₂ , x ₂₃ , x ₂₄ , x ₂₅ , x ₂₆ }, M = {3 2 3 2 2 2 0 0 0 1}.

Комплексный показатель вычисляется аналогично предыдущему примеру и равняется 15.

Таким образом, предложенный авторами подход представления динамических структур данных позволяет создавать информационные системы с изменяемой структурой информации об объектах предметной области и её обработки на уровне региона. Описанные в статье алгоритмы могут использоваться в разработке автоматизированных систем с динамическими структурами, создаваемых на базе предложенного подхода, для вычисления комплексных показателей при обработке статистической информации.

В развитие данного подхода планируется проведение дальнейших исследований: выявление структуры графа представления показателей, особенностей его построения и алгоритмов обхода этого графа; исследование возможностей хранения графов показателей, классификаторов и фактографических данных в системах управления базами данных в неизменном виде и разработка методик работы с элементами графов в этих системах; исследование возможных способов автоматической обработки фактографических данных с целью выявления недостоверных данных, новых комплексных показателей и новых классов данных для дальнейшего их анализа.