Алгоритмы расчета распространения света в свободном пространстве без использования алгоритма быстрого преобразования Фурье

Сложившаяся к настоящему моменту практика моделирования распространения светового поля предполагает использование алгоритма быстрого преобразования Фурье (БПФ) как основного инструмента для расчёта преобразований Фурье и Френеля, в оптике соответствующих прохождению светом линзы и некоторого расстояния в свободном пространстве соответственно. Этот широко распространённый и постоянно применяемый алгоритм позволяет быстро рассчитывать преобразование Фурье (затраты прямо пропорциональны количеству элементов обрабатываемого массива). В данной работе будут рассмотрены альтернативные способы расчета преобразований, не использующие алгоритма БПФ.

Будем, не сужая общности выводов, рассматривать двумерный (2D) случай, поскольку именно он встречается нам при моделировании распространения световых полей. Преобразование Фурье в декартовых координатах для 2D случая имеет вид: и ( ^ , n ) = ; да да

=к л и (

J -да -да

У ) exp - if ( x - ' y n ) dxdy = F ( и ( x,y ))

, (1)

где и(x,y) - комплексная амплитуда светового поля в исходной плоскости преобразования, x,y - поперечные координаты в исходной плоскости преобразования,

U ( Z , П ) — комплексная амплитуда светового поля в результирующей плоскости преобразования,

Z,n — поперечные координаты в результирующей плоскости преобразования, f- числовой параметр, соответствующий фокусному расстоянию линзы, k=2п/X - числовой параметр, соответствующий волновому числу падающего монохроматического света,

X - длина волны света,

F (•) - оператор Фурье-преобразования.

Или в дискретной форме:

kNN

^Uj =y ZZ u nm exp

J n = 1 m = 1

Imk- ( in + jm ) h ² h ² ,

где h - шаг разбиения, т.е. размер единичного элемента изображения, где Im = V-T - мнимая единица.

Если реализовывать его для массива-изображения NxN элементов, применяя традиционный алгоритм, то мы имеем конструкцию из 4-х циклов, алгоритмически которую можно записать примерно так:

Цикл по i от 1 до N

{Цикл по j от 1 до N

{U[i][j] =0;

Цикл по m от 1 до N

{Цикл по n от 1 до N

{U[i][j]=U[i][j]+(k/f)*u(m,n)* exp(-(Im*k/f)*((im+jn)/h2)); }

}

U[i][j] = (k/f)*U[i][j]*h2;

}

}, где Im - мнимая единица, u[i][j] - числовой массив комплексной амплитуды исходного изображения,

U[i][j] - массив результирующего изображения, h - шаг разбиения изображения, h = L / N , где L - размер стороны изображения.

Как видно, при увеличении числа отсчетов изображения N , здесь наблюдается рост вычислительных затрат, приблизительно пропорциональный N ⁴, что делает этот метод практически непригодным для расчёта больших изображений (например, из нескольких тысяч элементов при нынешнем уровне развития вычислительной техники).

Не вдаваясь в алгоритмические тонкости, отметим, что метод БПФ, как уже было сказано, работает гораздо быстрее и эффективнее, однако привносит в результат некоторые искажения, наиболее заметным из которых является несоответствие масштабов исходного и результирующего изображения. Это не играет большой роли при использовании его для моделирования работы сферической линзы, однако проявляется при моделировании распространения света в свободном пространстве как отсутствие расхождения световых пучков, что уже является серьёзным недостатком.

1. Преобразование Френеля

Преобразование Френеля и (^, n ,z ) = = -^—exp (ikz) 2nz to to j u (x,y) exp -to -to k-((x - ^)2 +(y - n)2) dxdy = 2 z

= Fr ( u ( x,y )) .

традиционно используется для описания распространения света в свободном пространстве на расстояниях z>>L. Как правило, постоянный фазовый множитель нас не интересует, поэтому из рассмотрения исключается быстро осциллирующая компонента exp( ikz ). Здесь z – расстояние распространения света, Fr (•) – оператор преобразования Френеля.

В дискретной форме:

^Uj =

Imk        N N

=---exp (Im kz )E E u

^{2 n} z              n = 1 m = 1

nm

exp

Im k        2          2 2

- -2z- ((i - n) + (j - m) )h

h ² .         (4)

Оно может быть представлено через преобразование Фурье:

U(x,y,z) =

ik .     Г ik I21 ..21

= — ^exp^(ikz)^exp — ( ^ +n )

to

to

И ТТ Z    x ^ik 2 . 2 1

U 0 (u,v)exp —( x + y )

exp -—( x ^+ y n ) dxdy = z

-to

^ik               I ^ik (21 . „2'1

= 2— exp(ikz)exp 2z- ( ^ +n )

Irr ,         i^k i 2.2 1

F < U 0 (u,v)exp — ( x² + y )

I                     2 z ^v

= Fr ( u ( x,y ))

Как правило, численная реализация производится с использованием метода БПФ, поскольку прямая реализация также требует использования конструкции из 4-х циклов:

Цикл по i от 1 до N

{Цикл по j от 1 до N

{U[i][j] =0;

Цикл по m от 1 до N

{Цикл по n от 1 до N

{U[i][j]=U[i][j]+exp((Im*k/(2*PI*z))* ((m-i)2+(n-j)2)/h2)*u(m,n); }

}

U[i][j]=(Im*k/(2*PI*z))*U[i][j]*h2;

} }.

Можно предложить несколько приемов, позволяющих уменьшить количество производимых вычислений. Как правило, мы имеем дело со световыми полями-изображениями, энергия которых сконцентрирована на сравнительно небольшой площади, как правило, в центральной области. На практике это означает, что значительная часть это означает, что значительная часть элементов изображения (как правило, большая часть) – нулевые. Поскольку для алгоритма безразлично, какие из циклов будут внешними, а какие – внутренними, мы можем вынести наружу циклы по переменным исходной плоскости изображения (i,j). Перед началом расчета вклада пикселя u[i][j] в результирующее изображение путем выполнения циклов по n и m нужно поставить проверку на наличие в u[i][j] ненулевого значения. Таким образом, можно в несколько (до 10) раз сократить вычислительные затраты.

Наибольшую «стоимость» по вычислительным затратам имеет расчет значения экспоненты от комплексного аргумента. При этом экспонента принимает N x N=N ² значений. Таким образом, мы имеем лишних N ² вычислений экспоненты. Решить эту проблему можно путем создания массива-буфера заранее рассчитанных значений экспоненты. При этом вычислительные затраты сокращаются ещё более значительно.

При вычислении преобразования Френеля на сравнительно малых дистанциях ( z ~ L ) мы сталкиваемся с проблемой необходимости увеличения числа отсчетов изображения для получения удовлетворительного результата. В противном случае изображение «рассыпается» в некую случайную картину. Это связано с наличием множителя ( ik /2 z ) h ² в подынтегральной экспоненте. При уменьшении z этот множитель соответственно вырастает настолько, что начинает значительно превышать 2 π . Таким образом, аргумент экспоненты даже на двух соседних отсчетах принимает существенно различные значения. Фактически, мы имеем дело со случайно меняющейся величиной – подынтегральным множителем. Естественно, в таких условиях нельзя говорить о достижении какой-то точности результата. При увеличении числа отсчетов изображения ситуация на некоторое время нормализуется в связи с уменьшением шага разбиения изображения h . Однако подобные меры обходятся несообразно дорого (вычислительные затраты, как уже говорилось, растут пропорционально N ⁴) и вряд ли могут быть признаны удовлетворительными как при современном уровне развития вычислительной техники, так и в обозримом будущем.

Однако можно предложить альтернативный метод решения обозначенной проблемы. Допустим, удовлетворительных результатов работы алгоритма можно достичь при увеличении числа осчетов изображения в K раз. Тогда дискретная форма (4) примет вид

^{Uii =} Imk exp ^{( Imk}z )

N x K N x K

E E u nm exp n =1 m =1

- Imk ( fiK - n) ² + (jK - m) ² ) h ²

2 z

h ²

при этом i,j€(1;NxK), h=L/(NK). В реальности мы имеем дело с измерительными приборами со строго фиксированным числом отсчетов. Таким образом,, исходный массив unm будет по-прежнему иметь NxN реальных значений, а остальные N2(K2-1) будут лишь их дублями:

u pq e [ iK + 1 ; ( i + 1 ) K ] = u jj                         (7)

Результирующее изображение ( N x K )² также не имеет практического применения. На самом деле, нам нужно лишь изображение NxN элементов

(i + 1 )K ( j + 1 )K

I I U pq

_!         p = iK + 1 q = jK + 1

^Uij = U pq] =         2       ,                ⁽⁸⁾

K где Uij – элементы финального изображения, размером NxK,

U pq – элементы промежуточного изображения, размером NK x NK .

Исходя из (7) и (8), расчет преобразования Френеля для изображения NK x NK отсчетов можно свести к расчету для изображения N x N отсчетов с усредненными значениями подынтегральной экспоненты – ядра преобразования

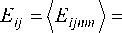
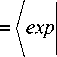
- ImZk- ( (iK - n) ² + (jK - m) ² h h

( i^K ⁽ j у)      ( Imk L x 2 / yV₂

Z I expl-——((iK - n) + (jK - m) j n = iK+1 m=jK+1    V 2 z

Аргумент экспоненты – тоже имеет квадратичную форму, поэтому можно рассчитать заранее матрицу её значений размером N x N = N ². Можно заметить, что матрица значений экспоненциального ядра преобразования симметрична относительно главной диагонали, следовательно вычислительные затраты на её расчет можно сократить вдвое.

Приближение сферических волн

F( in z) --f-Jf ff^AMex#

2n J J           Л2

-J ik

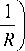
dxdy ,

R =V ^{( i} - ^{x) 2 + ( n} - ^{y) 2 +} z ^{2                  (12)}

по точности эквивалентно расчету через разложение по плоским волнам и является наиболее точным из достижимых в рамках скалярной теории. Оно применимо при z>2λ.

В дискретной форме:

NN u, =—УУи„„ ij                     nm

^{2 П} n = 1 m = 1

exp ^[ ImkR ij, nm ^]

R ²

ij nm

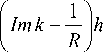
R j,nm = V ( ( i - n ) ² + ( j - m ) ² ) h ² + z ² -               (13)

Ядро преобразования также имеет квадратичную форму и может быть представлено матрицей N x N = N ², симметричной относительно главной диагонали.

Заключение

В работе рассмотрены альтернативные способы вычисления преобразований Френеля, Кирхгофа и сферических волн. Предложены методы оптимизации и сокращения вычислительных затрат. Вышеописанные методы подтвердили свою эффективность, будучи реализованы на практике. Предложенное решение проблемы расчета преобразования Френеля на ближних дистанциях без увеличения числа отсчетов изображения позволяет существенно расширить границы применимости данного алгоритма.

Работа выполнена при поддержке Министерства образования РФ, Администрации Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также грантов президента Российской Федерации МД-209.2003.01 и НШ-1007.2003.